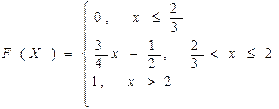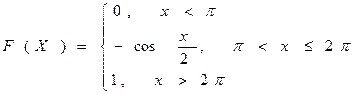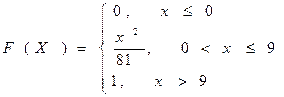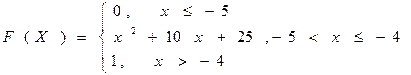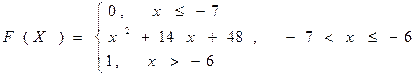Курс лекций по теории статистики

 

до виконання комплексного практичного індивідуального завдання (КПІЗ) з дисципліни “ Теорія ймовірностей та математична статистика ”

 

студента другого курсу групи Фвн – 21

професійна орієнтація “Фінанси”

 

 

____________________________________________________

ПІБ

 

Викладач – к.п.н., доцент Рум’янцева Катерина Євгеніївна

 

Графік виконання завдання та його оцінка:

 

Етапи	Зміст завдання	дата	Оцінка (за 100 бальною шкалою)	Підпис викладача
Перший	Завдання № 1	до 10 жовтня 2014 р.
Другий	Завдання № 2	до 13 листопада 2014 р.
Третій	Завдання № 3	до 27 листопада 2014 р.
Четвертий	Захист роботи	До 1 грудня 2014 р.

 

 

Робочий зошит виданий	Загальна оцінка
Дата	Варіант	Підпис викладача	Оцінка	Підпис викладача

 

Вінниця – ВННІЕ ТНЕУ – 2014

1. Структура залікового кредиту:

 

Перший заліковий кредит
Заліковий модуль 1	Заліковий модуль 2	Заліковий модуль 3 (ректорська контрольна робота)	Заліковий модуль 4 (підсумкова оцінка за КПІЗ)	Заліковий модуль 5 (письмовий екзамен)	Разом
тиждень 7	тиждень 17	тиждень 16	тиждень 18

 

2. Варіанти завдань:

 

ЗАВДАННЯ № 1.

Виробник радіоелектронного обладнання закуповує n інтегральних мікросхем, кожна з яких з імовірністю р може виявитись несправною. Позначимо події:

А - „серед n мікросхем рівно m1 несправних”;

В - „серед n мікросхем несправних більше m2, але менше m3 ”;

С - „серед n мікросхем несправних менше m4”.

Знайти імовірність заданих подій, якщо:

Варіант	n	p	m1	m2	m3	m4
		0,4
		0,13
		0,14
		0,15
		0,16		14-
		0,17
		0,18
		0,19
		0,2
		0,21
		0,22
		0,23
		0,24
		0,25
		0,26
		0,27
		0,28
		0,29
		0,3
		0,31
		0,32
		0,33
		0,34
		0,35
		0,36
		0,13
		0,12
		0,23
		0,14
		0,15

ЗАВДАННЯ № 2.

Випадкова величина Х задана функцією розподілу F (х). Знайти:

а) густину розподілу ймовірності;

б) числові характеристики цієї випадкової величини Х: m (x), D (x), E (x);

в) побудувати графіки функцій F (x), f (x);

г) ймовірність того, що випадкова величина прийме значення в інтервалі (а, b).

№ варіанту	F(X)	(a;b)
		(2;7)
		(-6;-0.3)
		(-13;-1)
		(2;10)
		(3;19)
		(-4;2.3)
		(7;16)
		(3.3;8)
		(-3;6)
		(5;18)
		(6;13)
		(5.4;10)
		(1;9)
		(2;6)
		(-2;4)
		(8.5;10)
		(3;13)
		(-7;1.5)
		(0.5;6)
		(-2.3;0)
		(-6;1)
		(-3;13)
		(-16;-5.4)
		(-10;-6.2)
		(-6;0)

ЗАВДАННЯ № 3.

Задано генеральну сукупність, яка характеризує річний прибуток фермерів (1000гр.). Зробити вибірку з 20 елементів та виконати такі дії:

1) побудувати статистичний розподіл вибірки та його емпіричну функцію розподілу;

2) обчислити числові характеристики вибірки;

3) побудувати полігони частот і відносних частот та гістограму, розбивши інтервали на чотири рівних підінтервали;

4) знайти моду, медіану та розмах варіацій.

 

№ варінта
	7 10 9 10 11 12 13 14 15 13 14 15 14 16 12 14 16 16 15 7
	10 11 12 13 14 15 13 14 15 14 16 12 14 16 16 15 7 5 7 8
	13 14 15 13 14 15 14 16 12 14 16 16 15 7 5 7 8 5 7 9
	13 14 15 14 16 12 14 16 16 15 7 5 7 8 5 7 9 10 9 8
	14 16 12 14 16 16 15 7 5 7 8 5 7 9 10 9 8 4 7 8
	14 16 16 15 7 5 7 8 5 7 9 10 9 8 4 7 8 10 9 4
	15 7 5 7 8 5 7 9 10 9 8 4 7 8 10 9 4 8 11 9
	7 8 5 7 9 10 9 8 4 7 8 10 9 4 8 11 9 11 8 10
	7 8 5 7 9 10 9 8 4 7 8 10 9 4 8 11 9 11 8 10
	7 9 10 9 8 4 7 8 10 9 4 8 11 9 11 8 10 12 9
	9 8 4 7 8 10 9 4 8 11 9 11 8 10 12 9 12 7 6 8
	7 8 10 9 4 8 11 9 11 8 10 12 9 12 7 6 8 5 3 6
	9 4 8 11 9 11 8 10 12 9 12 7 6 8 5 3 6 9 10 6
	11 9 11 8 10 12 9 12 7 6 8 5 3 6 9 10 6 5 11 9
	8 10 12 9 12 7 6 8 5 3 6 9 10 6 5 11 9 7 6 7
	9 12 7 6 8 5 3 6 9 10 6 5 11 9 7 6 7 10 9 8
	6 8 5 3 6 9 10 6 5 11 9 7 6 7 10 9 8 11 6 5
	3 6 9 10 6 5 11 9 7 6 7 10 9 8 11 6 5 10 8 7
	10 6 5 11 9 7 6 7 10 9 8 11 6 5 10 8 7 6 9 8
	11 9 7 6 7 10 9 8 11 6 5 10 8 7 6 9 8 10 7 10
	6 7 10 9 8 11 6 5 10 8 7 6 9 8 10 7 10 12 7 8
	9 8 11 6 5 10 8 7 6 9 8 10 7 10 12 7 8 10 12 11
	6 5 10 8 7 6 9 8 10 7 10 12 7 8 10 12 11 9 10 8
	8 7 6 9 8 10 7 10 12 7 8 10 12 11 9 10 8 11 12 14
	9 8 10 7 10 12 7 8 10 12 11 9 10 8 11 12 14 10 8 14
	7 10 12 7 8 10 12 11 9 10 8 11 12 14 10 8 14 7 10 8
	7 8 10 12 11 9 10 8 11 12 14 10 8 14 7 10 8 13 10 9
	12 11 9 10 8 11 12 14 10 8 14 7 10 8 12 10 9 13 12 14
	10 8 11 12 14 10 8 14 7 10 8 13 10 9 13 12 14 10 12 14
	12 14 10 8 14 7 10 8 13 10 9 13 12 14 10 12 14 15 13 14

3. Критерії оцінювання:

За шкалою Університету	Критерії оцінювання
90-100	Отримано правильну відповідь з обґрунтуванням усіх ключових моментів розв'язування
85-89	Наведено логічно правильну послідовність кроків розв'язування. Деякі з ключових моментів розв'язування обґрунтовано недостатньо. Можливі 1–2 помилки або описки в обчисленнях, перетвореннях, які не впливають на правильність подальшого розв’язування, наявність неточностей у побудові діаграм, що не вплинуло на правильність розв’язку. Отримана відповідь може бути неправильною.
75-84	Наведено логічно правильну послідовність кроків розв'язування. Незакінчене розв’язання завдання, виконавши при цьому не менше половини логічних кроків; отримана відповідь може бути неправильною або неповною (розв’язана правильно лише частина завдання).
60-74	У правильній послідовності розв'язування відсутні деякі етапи. Допущені грубі помилки (більше однієї). Ключові моменти розв’язування не обґрунтовано. Діаграми побудовані частково або не побудовані взагалі. Отримана відповідь неправильна або завдання розв'язане неповністю.
1-59	Якщо студент не приступив до розв’язування завдань.

4. Література:

 

1. Барковський В.В., Барковська Н.В. Математика для економістів. Вища математика. – К.:Національна академія управління, 1999 р.—399 с.

2. Барковський В. В., Барковська Н. В., Лопатін О. К. Математика для економістів: Теорія імовірностей та математична статистика. – К.: Національна академія управління. 1997. – 255с.

3. Бобик О.І., Берегова Г.І., Копитко Б.І. Теорія ймовірності та математична статистика. – Підручник. – К.: ВД “Професіонал”, 2007. – 560 с.

4. Бугір М.К. Математика для економістів. – Тернопіль: Підручники & посібники, 1998.- 190 с.

5. Бугір М. К. Теорія ймовірності та математична статистика. Тернопіль: Підручники & посібники. 1998. – 176с.

6. Бугір М. К. Практикум з теорії ймовірності та математичної статистики. Тернопіль: Підручники & посібники. 1998. – 176с.

7. Булига К.Б, Барановська Л.В. Практикум з теорії ймовірностей та математичної статистики: Навч. Посіб. – К.:Європ. ун-т, 2000.–173с.

8. Высшая математика с основами математической статистики (Учебник для фин. и экон. вузов и фак.). М.: Высшая школа, 1965.

9. Гмурман В. Е. Теория вероятностей и математическая статистика. Изд. 4 доп. Учебное пособие для вузов. – М.: Высш. шк. – 1972. – 368с.

10. Гмурман В. Е. Руководство к решению задач по теории вероятностей и математической статистике. – М.: Высш. шк. – 1979. – 400с.

11. Гнеденко Б.В. Курс теории вероятностей. – М.: Наука, 961.

12. Єрьоменко В.О., Шинкарик М.І. Теорія ймовірностей. Навчальний посібник для студентів економічних спеціальностей. – Тернопіль: Економічна думка, 2002. – 176 с.

13. Єрьоменко В.О., Шинкарик М.І. Математична статистика. Навчальний посібник для студентів економічних спеціальностей. – Тернопіль: Економічна думка, 2001. – 247 с.

14. Жлуктенко В.С., Наконечний С.І. Теорія ймовірностей і математична статистика: навч.-метод. Посібник. У 2 ч. – К.: КНТЕУ, 2000. – 304 с.

15. Захарченко Н.В., Козловський А.В., Погріщук Б.В. Теорія імовірностей та математична статистика. Методичні вказівки для студентів.ВІЕ ТАНГ. 2004. – 72 с.

16. Карасев А. И. Теория вероятностей и математическая статистика. – М.: Статистика. 1977. – 279с.

17. Клепко В.Ю. Вища математика в прикладах і задачах: навч. посіб. / В.Ю. Клепко, В.Л. Голець. – 2-е вид., переробл. і доп. – К.: Центр навч. л-ри, 2006. – 600 с.

18. Математика в экономике: учеб.: В 2-х ч. Ч.2. / А.С. Солодовников и др – М.: Финансы и статистика, 2000. – 374 с.

19. Ніколюк П.К. Математика для економістів. Навчальний посібник / П.К. Ніколюк, Б.В. Погріщук. – Тернопіль: ФОП Кошлатий Є.А., 2006. – 284 с.

Курс лекций по теории статистики

 

 

 

СОДЕРЖАНИЕ

Введение. 6

Глава 1. Статистическое наблюдение. 7

1.1. Основные формы, виды и способы статистического наблюдения. 7

1.2. Программно - методологические вопросы статистического наблюдения 12

1.3. Основные организационные вопросы статистического наблюдения 16

1.4. Точность статистического наблюдения и ее контроль. 17

Глава 2. Статистическая сводка и группировка. 23

2.1. Задачи сводки и ее содержание. 23

2.2. Виды статистических группировок. 24

2.3. Принципы построения статистических группировок и классификаций 25

2.4. Сравнимость статистических группировок. Вторичная группировка 36

2.5. Статистическая таблица и ее элементы.. 37

2.6. Виды таблиц по характеру подлежащего. 39

2.7. Виды таблиц по разработке сказуемого. 42

2.8. Основные правила построения таблиц. 43

2.9. Чтение и анализ таблицы.. 45

Глава 3. Абсолютные и относительные статистические показатели. 47

3.1. Классификация статистических показателей. 47

3.2. Абсолютные показатели. 49

3.3. Относительные показатели. 51

Глава 4. Графическое изображение статистических данных. 58

4.1. Понятие о статистическом графике. Элементы статистического графика 58

4.2. Классификация видов графиков. 61

4.3. Диаграммы сравнения. 64

4.4. Диаграммы структуры.. 68

4.5. Диаграммы динамики. 71

4.6. Статистические карты. 77

 

Глава 5. Средние показатели. 79

5.1. Сущность средних показателей. 79

5.2. Средняя арифметическая и ее свойства. 81

5.3. Другие виды средних. 87

5.4. Структурные средние. 90

Глава 6. Анализ вариации. 95

6.1. Основные показатели вариации. 95

6.2. Использование показателей вариации в анализе взаимосвязей. 97

Глава 7. Выборочное наблюдение. 101

7.1. Выборочное наблюдение как важнейший источник статистической информации. 101

Символы основных характеристик параметров. 103

7.2. Основные способы формирования выборочной совокупности. 103

7.3. Определение необходимого объема выборки. 114

7.4. Оценка результатов выборочного наблюдения и распространение их на генеральную совокупность. 116

7.5. Малая выборка. 119

Глава 8. Статистическое изучение взаимосвязи социально-экономических явлений 121

8.1. Причинность, регрессия, корреляция. 121

8.2. Парная регрессия на основе метода наименьших квадратов и метода группировок. 125

8.3. Множественная (многофакторная) регрессия. 128

8.4. Собственно-корреляционные параметрические методы изучения связи. 131

8.5. Принятие решений на основе уравнений регрессии. 135

8.6. Методы изучения связи качественных признаков. 137

8.7. Ранговые коэффициенты связи. 141

Глава 9. Статистическое изучение динамики социально-экономических явлений 145

9.1. Понятие и классификации рядов динамики. 145

9.2. Сопоставимость уровней и смыкание рядов динамики. 147

9.3. Показатели изменения уровней ряда динамики. 150

9.4. Методы анализа основной тенденции (тренда) в рядах динамики 157

9.5. Методы выявления сезонной компоненты.. 162

9.6. Элементы прогнозирования и интерполяции. 164

Глава 10. Статистический анализ структуры.. 167

10.1. Понятие структуры и основные направления ее исследования 167

10.2. Частные показатели структурных сдвигов. 168

10.3. Обобщающие показатели структурных сдвигов. 171

10.4. Показатели концентрации и централизации. 174

Глава 11. Индексы.. 178

11.1. Общие понятия об индексах. 178

11.2. Агрегатные индексы.. 179

11.3. Сводные индексы в средней арифметической и средней гармонической формах. 183

11.4. Системы индексов. 185

11.5. Индексы постоянного и переменного состава. 186

Заключение. 188

Рекомендуемая литература. 189