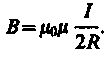Применение к расчету магнитного поля
Магнитное поле постоянных токов различной формы изучалось французскими учеными Ж. Био (1774—1862) и Ф. Саваром (1791—1841). Результаты этих опытов были обобщены выдающимся французским математиком и физиком П. Лапласом. Закон Био — Савара — Лапласа для проводника с током I, элемент d l которого создает в некоторой точке А(рис. 164) индукцию поля dB, записывается в виде
где dl — вектор, по модулю равный длине dl элемента проводника и совпадающий по направлению с током, г — радиус-вектор, проведенный из элемента d/ проводника в точку А поля, r — модуль радиуса-вектора г. Направление dB перпендикулярно dl и г, т. е. перпендикулярно плоскости, в которой они лежат, и совпадает с касательной к линии магнитной индукции. Это направление может быть найдено по правилу нахождения линий магнитной индукции (правилу правого винта): направление вращения головки винта дает направление dB, если поступательное движение винта соответствует направлению тока в элементе.
Рис. 164
Модуль вектора dB определяется выражением
где a — угол между векторами dl и г. Для магнитного поля, как и для электрического, справедлив принцип суперпозиции: магнитная индукция результирующего поля, создаваемого несколькими токами или движущимися зарядами, равна векторной сумме магнитных индукций складываемых полей, создаваемых каждым током или движущимся зарядом в отдельности:
Расчет характеристик магнитного поля (В и Н) по приведенным формулам в общем случае сложен. Однако если распределение тока имеет определенную сим метрию, то применение закона Био — Савара — Лапласа совместно с принципом суперпозиции позволяет просто рассчитать конкретные поля. Рассмотрим два примера. 1.Магнитное поле прямого тока — тока, текущего по тонкому прямому проводу бесконечной длины (рис. 165). В произвольной точке А, удаленной от оси проводника на расстояние R, векторы dB от всех элементов тока имеют одинаковое направление, перпендикулярное плоскости чертежа («к нам»). Поэтому сложение векторов dB можно заменить сложением их модулей. В качестве постоянной интегрирования выберем угол а (угол между векторами dl и г), выразив через него все остальные величины.
Рис. 165
Из рис. 165 следует, что
(радиус дуги CD вследствие малости d l равен r, и угол FDCпо этой же причине можно считать прямым). Подставив эти выражения в (110.2), получим, что магнитная индукция, создаваемая одним элементом проводника, равна
Так как угол a для всех элементов прямого тока изменяется в пределах от 0 до p, то, согласно (110.3) и (110.4),
Следовательно, магнитная индукция поля прямого тока
2. Магнитное поле в центре кругового проводника с током (рис. 166). Как следует из рисунка, все элементы кругового проводника с током создают в центре магнитные поля одинакового направления — вдоль нормали от витка. Поэтому сложение век торов dB можно заменить сложением их модулей.
Рис. 166
Так как все элементы проводника перпендикулярны радиусу-вектору (sina = l) и расстояние всех элементов проводника до центра кругового тока одинаково и равно R, то, согласно (110.2),
Следовательно, магнитная индукция поля в центре кругового проводника с током
|

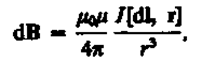 (110.1)
(110.1)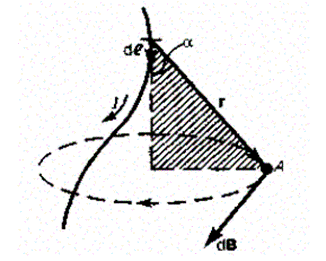
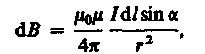 (110.2)
(110.2)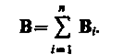 (110.3)
(110.3)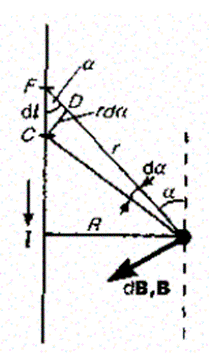
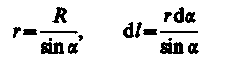
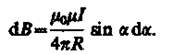 (110.4)
(110.4)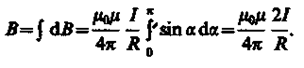
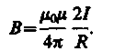 (110.5)
(110.5)