Максвелл ввел понятие полного тока,равного сумме токов проводимости (а также конвекционных токов) и смещения.Плотность полного тока 16 страница
Статистическое толкование волн де Бройля (см. § 216) и соотношение неопределенностей Гейзенберга (см. § 215) привели к выводу, что уравнением движения в квантовой механике, описывающим движение микрочастиц в различных силовых полях, должно быть уравнение, из которого бы вытекали наблюдаемые на опыте волновые свойства частиц. Основное уравнение должно быть уравнением относительно волновой функции Y(х, у, z, t), так как именно она, или, точнее, величина |Y|2, определяет вероятность пребывания частицы в момент времени t в объеме d V, т. е. в области с координатами х и x+dx, у и y+dy, z и z+dz. Taк как искомое уравнение должно учитывать волновые свойства частиц, то оно должно быть волновым уравнением, подобно уравнению, описывающему электромагнитные волны. Основное уравнение нерелятивистской квантовой механики сформулировано в 1926 г. Э. Шредингером. Уравнение Шредингера, как и все основные уравнения физики (например, уравнения Ньютона в классической механике и уравнения Максвелла для электромагнитного поля), не выводится, а постулируется. Правильность этого уравнения подтверждается согласием с опытом получаемых с его помощью результатов, что, в свою очередь, придает ему характер закона природы. Уравнение Шредингера имеет вид
где ћ = h /(2p), т— масса частицы, D—оператор Лапласа Уравнение (217.1) справедливо для любой частицы (со спином, равным 0; см. § 225), движущейся с малой (по сравнению со скоростью света) скоростью, т. е. со скоростью v <<с. Оно дополняется условиями, накладываемыми на волновую функцию: 1) волновая функция должна быть конечной, однозначной и непрерывной (см. § 216); 2) производные Чтобы прийти к уравнению Шредингера, рассмотрим свободно движущуюся частицу, которой, согласно идее де Бройля, сопоставляется плоская волна. Для простоты рассмотрим одномерный случай. Уравнение плоской волны, распространяющейся вдоль оси х, имеет вид (см. § 154)
(учтено, что w = E/ћ, k=p/ћ). В квантовой механике показатель экспоненты берут со знаком минус, но поскольку физический смысл имеет только |Y|2, то это (см. (217.2)) несущественно. Тогда
откуда
Используя взаимосвязь между энергией Е и импульсом р (E=p 2 /( 2 m)) и подставляя выражения (217.3), получим дифференциальное уравнение
которое совпадает с уравнением (217.1) для случая U= 0 (мы рассматривали свободную частицу). Если частица движется в силовом поле, характеризуемом потенциальной энергией U, то полная энергия Е складывается из кинетической и потенциальной энергий. Проводя аналогичные рассуждения и используя взаимосвязь между Е и р (для данного случая p 2/(2 m)= E–U), прядем к дифференциальному уравнению, совпадающему с (217.1). Приведенные рассуждения не должны восприниматься как вывод уравнения Шредингера. Они лишь поясняют, как можно прийти к этому уравнению. Доказательством правильности уравнения Шредингера является согласие с опытом тех выводов, к которым оно приводит. Уравнение (217.1) является общим уравнением Шредингера. Его также называют уравнением Шредингера, зависящим от времени. Для многих физических явлений, происходящих в микромире, уравнение (217.1) можно упростить, исключив зависимость Y от времени, иными словами, найти уравнение Шредингера для стационарных состояний — состояний с фиксированными значениями энергии. Это возможно, если силовое поле, в котором частица движется, стационарно, т. е. функция U=U(x, у, z) не зависит явно от времени и имеет смысл потенциальной энергии. В данном случае решение уравнения Шредингера может быть представлено в виде произведения двух функций, одна из которых есть функция только координат, другая — только времени, причем зависимость от времени выражается множителем
где Е — полная энергия частицы, постоянная в случае стационарного поля. Подставляя (217.4) в (217.1), получим
откуда после деления на общий множитель
Уравнение (217.5) называется уравнением Шредингера для стационарных состояний. В это уравнение в качестве параметра входит полная энергия Е частицы. В теории дифференциальных уравнений доказывается, что подобные уравнения имеют бесчисленное множество решений, из которых посредством наложения граничных условий отбирают решения, имеющие физический смысл. Для уравнения Шредингера такими условиями являются условия регулярности волновых функций: волновые функции должны быть конечными, однозначными и непрерывными вместе со своими первыми производными. Таким образом, реальный физический смысл имеют только такие решения, которые выражаются регулярными функциями y. Но регулярные решения имеют место не при любых значениях параметра Е, а лишь при определенном их наборе, характерном для данной задачи. Эти значения энергии называются собственными. Решения же, которые соответствуют собственным значениям энергии, называются собственными функциями. Собственные значения Е могут образовывать как непрерывный, так и дискретный ряд. В первом случае говорят о непрерывном, или сплошном, спектре, во втором — о дискретном спектре. § 218. Принцип причинности в квинтовой механике Из соотношения неопределенностей часто делают вывод о неприменимости принципа причинности к явлениям, происходящим в микромире. При этом основываются на следующих соображениях. В классической механике, согласно принципу причинности — принципу классического детерминизма, по известному состоянию системы в некоторый момент времени (полностью определяется значениями координат и импульсов всех частиц системы) и силам, приложенным к ней, можно абсолютно точно задать ее состояние в любой последующий момент. Следовательно, классическая физика основывается на следующем понимании причинности: состояние механической системы в начальный момент времени с известным законом взаимодействия частиц есть причина, а ее состояние в последующий момент — следствие. С другой стороны, микрообъекты не могут иметь одновременно и определенную координату, и определенную соответствующую проекцию импульса (задаются соотношением неопределенностей (215.1)), поэтому и делается вывод о том, что в начальный момент времени состояние системы точно не определяется. Если же состояние системы не определено в начальный момент времени, то не могут быть предсказаны и последующие состояния, т. е. нарушается принцип причинности. Однако никакого нарушения принципа причинности применительно к микрообъектам не наблюдается, поскольку в квантовой механике понятие состояния микрообъекта приобретает совершенно иной смысл, чем в классической механике. В квантовой механике состояние микрообъекта полностью определяется волновой функцией Y(x, у, z, t), квадрат модуля которой |Y (x, у, z, t)|2 задает плотность вероятности нахождения частицы в точке с координатами х, у, z. В свою очередь, волновая функция Y(х, у, z, t) удовлетворяет уравнению Шредингера (217.1), содержащему первую производную функции Y по времени. Это же означает, что задание функции Y0 (для момента времени t 0) определяет ее значение в последующие моменты. Следовательно, в квантовой механике начальное состояние Y0 есть причина, а состояние Y в последующий момент — следствие. Это и есть форма принципа причинности в квантовой механике, т. е. задание функции Y0 предопределяет ее значения для любых последующих моментов. Таким образом, состояние системы микрочастиц, определенное в квантовой механике, однозначно вытекает из предшествующего состояния, как того требует принцип причинности. § 219. Движение свободной частицы Свободная частица — частица, движущаяся в отсутствие внешних полей. Так как на свободную частицу (пусть она движется вдоль оси х) силы не действуют, то потенциальная энергия частицы U (x) = const и ее можно принять равной нулю. Тогда полная энергия частицы совпадает с ее кинетической энергией. В таком случае уравнение Шредингера (217.5) для стационарных состояний примет вид
Прямой подстановкой можно убедиться в том, что частным решением уравнения (219.1) является функция y (х) = Аеikx, где А = const и k = const, с собственным значением энергии
Функция
(здесь Из выражения (219.2) следует, что зависимость энергии от импульса
оказывается обычной для нерелятивистских частиц. Следовательно, энергия свободной частицы может принимать любые значения (так как волновое число k может принимать любые положительные значения), т. е. ее энергетический спектр является непрерывным. Таким образом, свободная квантовая частица описывается плоской монохроматической волной де Бройля. Этому соответствует не зависящая от времени плотность вероятности обнаружения частицы в данной точке пространства
т. е. все положения свободной частицы в пространстве являются равновероятными. § 220. Частице в одномерной прямоугольной «потенциальной яме» с бесконечно высокими «стенками» Проведем качественный анализ решений уравнения Шредингера применительно к частице в одномерной прямоугольной «потенциальной яме» с бесконечно высокими «стенками». Такая «яма» описывается потенциальной энергией вида (для простоты принимаем, что частица движется вдоль оси х)
где l — ширина «ямы», а энергия отсчитывается от ее дна (рис. 296).
Уравнение Шредингера (217.5) для стационарных состояний в случае одномерной задачи запишется в виде
По условию задачи (бесконечно высокие «стенки»), частица не проникает за пределы «ямы», поэтому вероятность ее обнаружения (а следовательно, и волновая функция) за пределами «ямы» равна нулю. На границах «ямы» (при х= 0 и х= 1) непрерывная волновая функция также должна обращаться в нуль. Следовательно, граничные условия в данном случае имеют вид
В пределах «ямы» (0 £ х £ l) уравнение Шредингера (220.1) сведется к уравнению
или
где
Общее решение дифференциального уравнения (220.3):
Так как по (220.2) y (0)=0, то В =0. Тогда
Условие (220.2) y (l) =A sin kl = 0 выполняется только при kl = np, где n — целые числа, т. е. необходимо, чтобы
Из выражений (220.4) и (220.6) следует, что
т. е. стационарное уравнение Шредингера, описывающее движение частицы в «потенциальной яме» с бесконечно высокими «стенками», удовлетворяется только при собственных значениях Еn, зависящих от целого числа п. Следовательно, энергия Еn частицы в «потенциальной яме» с бесконечно высокими «стенками» принимает лишь определенные дискретные значения,т.е. квантуется. Квантованные значения энергии Еn называются уровнями энергии, а число п, определяющее энергетические уровни частицы, называется главным квантовым числом. Таким образом, микрочастица в «потенциальной яме» с бесконечно высокими «стенками» может находиться только на определенном энергетическом уровне Еn, или, как говорят, частица находится в квантовом состоянии n. Подставив в (220.5) значение k из (220.6), найдем собственные функции:
Постоянную интегрирования А найдем из условия нормировки (216.3), которое для данного случая запишется в виде
В результате интегрирования получим А =
Графики собственных функций (220.8), соответствующие уровням энергии (220.7) при n = 1, 2, 3, приведены на рис. 297, а. На рис. 297, 6 изображена плотность вероятности обнаружения частицы на различных расстояниях от «стенок» ямы, равная | yn (х)|2 = yn (х) y*n (х) для n= 1,2 и 3. Из рисунка следует, что, например, в квантовом состоянии с n =2 частица не может находиться в середине «ямы», в то времякакодинаково часто может пребывать в ее левой и правой частях. Такое поведение частицы указывает на то, что представления о траекториях частицы в квантовой механике несостоятельны. Из выражения (220.7) вытекает, что энергетический интервал между двумя соседними уровнями равен
Например, для электрона при размерах ямы l= 10–1 м (свободные электроны в металле) D En » 10–35 n Дж» 10–16 n эВ, т. е. энергетические уровни расположены столь тесно, что спектр практически можно считать непрерывным. Если же размеры ямы соизмеримы с атомными (l»10–10 м), то для электрона D En » 10–17 n Дж» 102 n эВ, т. е. получаются явно дискретные значения энергии (линейчатый спектр). Таким образом, применение уравнения Шредингера к частице в «потенциальной яме» с бесконечно высокими «стенками» приводит к квантованным значениям энергии, в то время как классическая механика на энергию этой частицы никаких ограничений не накладывает.
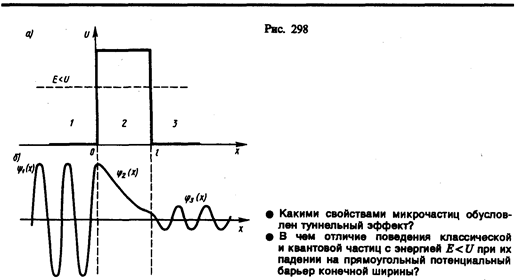
Кроме того, квантово-механическое рассмотрение данной задачи приводит к выводу, что частица «в потенциальной яме» с бесконечно высокими «стенками» не может иметь энергию меньшую, чем минимальная энергия, равная Из формул (220.9) и (220.7) следует, что при больших квантовых числах (n >>1) D En/En»2/ n <<1, т. е. соседние уровни расположены тесно: тем теснее, чем больше n. Если n очень велико, то можно говорить о практически непрерывной последовательности уровней и характерная особенность квантовых процессов — дискретность — сглаживается. Этот результат является частным случаем принципа соответствия Бора (1923), согласно которому законы квантовой механики должны при больших значениях квантовых чисел переходить в законы классической физики. Более общая трактовка принципа соответствия, имеющего огромную роль в современной физике, заключается в следующем: всякая новая, более общая теория, являющаяся развитием классической, не отвергает ее полностью, а включает в себя классическую теорию, указывая границы ее применения, причем в определенных предельных случаях новая теория переходит в старую. Так, формулы кинематики и динамики специальной теории относительности переходят при v << с в формулы механики Ньютона. Например, хотя гипотеза де Бройля приписывает волновые свойства всем телам, но в тех случаях, когда мы имеем дело с макроскопическими телами, их волновыми свойствами можно пренебречь, т. е. применять классическую механику Ньютона. § 221. Прохождение частицы сквозь потенциальный барьер. Туннельный эффект Рассмотрим простейший потенциальный барьер прямоугольной формы (рис. 298, а) для одномерного (по оси х) движения частицы. Для потенциального барьера прямоугольной формы высоты U и ширины l можем записать
При данных условиях задачи классическая частица, обладая энергией Е, либо беспрепятственно пройдет над барьером (при Е>U), либо отразится от него (при Е<U) и будет двигаться в обратную сторону, т. е. она не может проникнуть сквозь барьер. Для микрочастицы же, даже при Е>U, имеется отличная от нуля вероятность, что частица отразится от барьера и будет двигаться в обратную сторону. При E<U имеется также отличная от нуля вероятность, что частица окажется в области х>1, т. е. проникает сквозь барьер. Подобные, казалось бы, парадоксальные выводы следуют непосредственно из решения уравнения Шредингера, описывающего движение микрочастицы при условиях данной задачи.
Уравнение Шредингера (217.5) для стационарных состояний для каждой из выделенных на рис. 298, а области имеет вид
Общие решения этих дифференциальных уравнений:
В частности, для области 1 полная волновая функция, согласно (217.4), будет иметь вид
В этом выражении первый член представляет собой плоскую волну типа (219.3), распространяющуюся в положительном направлении оси х (соответствует частице, движущейся в сторону барьера), а второй — волну, распространяющуюся в противоположном направлении, т. е. отраженную от барьера (соответствует частице, движущейся от барьера налево). Решение (221.3) содержит также волны (после умножения на временной множитель), распространяющиеся в обе стороны. Однако в области 3 имеется только волна, прошедшая сквозь барьер и распространяющаяся слева направо. Поэтому коэффициент B 3 в формуле (221.3) следует принять равным нулю. В области 2 решение зависит от соотношений Е>U или Е<U. Физический интерес представляет случай, когда полная энергия частицы меньше высоты потенциального барьера, поскольку при Е<U законы классической физика однозначно не разрешают частице проникнуть сквозь барьер. В данном случае, согласно (221.1), q=ib — мнимое число, где
Учитывая значение q и B 3=0, получим решения уравнения Шредингера для трех областей в следующем виде:
В области 2 функция (221.5) уже не соответствует плоским волнам, распространяющимся в обе стороны, поскольку показатели степени экспонент не мнимые, а действительные. Можно показать, что для частного случая высокого и широкого барьера, когда bl >>1, B 2 » 0. Качественный характер функций y 1(х), y 2(х) и y 3(x) иллюстрируется на рис. 298, б, откуда следует, что волновая функция не равна нулю и внутри барьера, а в области 3, если барьер не очень широк, будет опять иметь вид волн де Бройля с тем же импульсом, т. е. с той же частотой, но с меньшей амплитудой. Следовательно, получили, что частица имеет отличную от нудя вероятность прохождения сквозь потенциальный барьер конечной ширины. Таким образом, квантовая механика приводит к принципиально новому специфическому квантовому явлению, получившему название туннельного эффекта, в результате которого микрообъект может «пройти» сквозь потенциальный барьер. Для описания туннельного эффекта используют понятие коэффициента прозрачности D потенциального барьера, определяемого как отношение плотности потока прошедших частиц к плотности потока падающих. Можно показать, что
Для того чтобы найти отношение | А 3 /А 1|2, необходимо воспользоваться условиями непрерывности y и y ' на границах барьера х =0 и х = l (рис. 298):
Эти четыре условия дают возможность выразить коэффициенты A 2, A 3, В 1 и В 2 через А 1. Совместное решение уравнений (221.6) для прямоугольного потенциального барьера дает (в предположении, что коэффициент прозрачности мал по сравнению с единицей)
где U — высота потенциального барьера, Е — энергия частицы, l — ширина барьера, D 0 — постоянный множитель, который можно приравнять единице. Из выражения (221.7) следует, что D сильно зависит от массы т частицы, ширины l барьера и от (U—E); чем шире барьер, тем меньше вероятность прохождения сквозь него частицы. Для потенциального барьера произвольной формы (рис. 299), удовлетворяющей условиям так называемого квазиклассического приближения (достаточно гладкая форма кривой), имеем
где U = U (x).
С классической точки зрения прохождение частицы сквозь потенциальный барьер при Е<U невозможно, так как частица, находясь в области барьера, должна была бы обладать отрицательной кинетической энергией. Туннельный эффект является специфическим квантовым эффектом. Прохождение частицы сквозь область, в которую, согласно законам классической механики, она не может проникнуть, можно пояснить соотношением неопределенностей. Неопределенность импульса D р на отрезке D х = l составляет D p>h/l. Связанная с этим разбросом в значениях импульса кинетическая энергия (D р)2/(2 m) может оказаться достаточной для того, чтобы полная энергия частицы оказалась больше потенциальной. Основы теории туннельных переходов заложены работами Л. И. Мандельштама и М. А. Леонтовича (1903—1981). Туннельное прохождение сквозь потенциальный барьер лежит в основе многих явлений физики твердого тела (например, явления в контактном слое на границе двух полупроводников), атомной и ядерной физики (например, a-распад, протекание термоядерных реакций). § 222. Линейный гармонический осциллятор в квантовой механике Линейный гармонический осциллятор — система, совершающая одномерное движение под действием квазиупругой силы, — является моделью, используемой во многих задачах классической и квантовой теории (см. § 142). Пружинный, физический и математический маятники — примеры классических гармонических осцилляторов. Потенциальная энергия гармонического осциллятора (см. (141.5)) равна
где w 0 — собственная частота колебаний осциллятора, т — масса частицы. Зависимость (222.1) имеет вид параболы (рис. 300), т. е. «потенциальная яма» в данном случае является параболической.
Амплитуда малых колебаний классического осциллятора определяется его полной энергией Е (см. рис. 16). В точках с координатами ± x max полная энергия Е равна потенциальной энергии. Поэтому с классической точки зрения частица не может выйти за пределы области (– x max, + x max). Такой выход означал бы, что ее потенциальная энергия больше полной, что абсурдно, так как приводит к выводу, что кинетическая энергия отрицательна. Таким образом, классический осциллятор находится в «потенциальной яме» с координатами – x max < х < x max «без права выхода» из нее. Гармонический осциллятор в квантовой механике — квантовый осциллятор — описывается уравнением Шредингера (217.5), учитывающим выражение (222.1) для потенциальной энергии. Тогда стационарные состояния квантового осциллятора определяются уравнением Шредингера вида
|

 (217.1)
(217.1)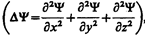 i — мнимая единица, U (х, у, z, t) — потенциальная функция частицы в силовом поле, в котором она движется, Y (х, у, z, t) — искомая волновая функция частицы.
i — мнимая единица, U (х, у, z, t) — потенциальная функция частицы в силовом поле, в котором она движется, Y (х, у, z, t) — искомая волновая функция частицы. должны быть непрерывны; 3) функция |Y|2 должна быть интегрируема; это условие в простейших случаях сводится к условию нормировки вероятностей (216.3).
должны быть непрерывны; 3) функция |Y|2 должна быть интегрируема; это условие в простейших случаях сводится к условию нормировки вероятностей (216.3). , или в комплексной записи
, или в комплексной записи 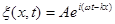 . Следовательно, плоская волна де Бройля имеет вид
. Следовательно, плоская волна де Бройля имеет вид (217.2)
(217.2)
 (217.3)
(217.3)
 , так что
, так что (217.4)
(217.4)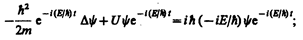
 и соответствующих преобразований придем к уравнению, определяющему функцию y:
и соответствующих преобразований придем к уравнению, определяющему функцию y: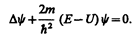 (217.5)
(217.5) (219.1)
(219.1) (219.2)
(219.2) представляет собой только координатную часть волновой функции Y(x, t). Поэтому зависящая от времени волновая функция, согласно (217.4),
представляет собой только координатную часть волновой функции Y(x, t). Поэтому зависящая от времени волновая функция, согласно (217.4), (219.3)
(219.3) и
и  ). Функция (219.3) представляет собой плоскую монохроматическую волну де Бройля (см. (217.2)).
). Функция (219.3) представляет собой плоскую монохроматическую волну де Бройля (см. (217.2)).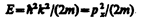



 (220.1)
(220.1) (220.2)
(220.2)
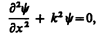 (220.3)
(220.3) (220.4)
(220.4)
 (220.5)
(220.5) (220.6)
(220.6) (220.7)
(220.7)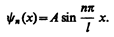

 , а собственные функции будут иметь вид
, а собственные функции будут иметь вид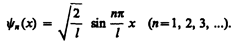 (220.8)
(220.8) (220.9)
(220.9)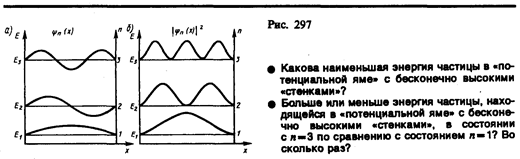
 . Наличие отличной от нуля минимальной энергии не случайно и вытекает из соотношения неопределенностей. Неопределенность координаты D х частицы в «яме» шириной l равна D x = l. Тогда, согласно соотношению неопределенностей (215.1), импульс не может иметь точное, в данном случае нулевое, значение. Неопределенность импульса D p»h/l. Такому разбросу значений импульса соответствует кинетическая энергия E min»(D p)2/(2 m) = h 2/(2 ml 2). Все остальные уровни (n >1) имеют энергию, превышающую это минимальное значение.
. Наличие отличной от нуля минимальной энергии не случайно и вытекает из соотношения неопределенностей. Неопределенность координаты D х частицы в «яме» шириной l равна D x = l. Тогда, согласно соотношению неопределенностей (215.1), импульс не может иметь точное, в данном случае нулевое, значение. Неопределенность импульса D p»h/l. Такому разбросу значений импульса соответствует кинетическая энергия E min»(D p)2/(2 m) = h 2/(2 ml 2). Все остальные уровни (n >1) имеют энергию, превышающую это минимальное значение.
 (221.1)
(221.1) (221.2)
(221.2)
 (221.3)
(221.3) (221.4)
(221.4)
 (221.5)
(221.5)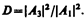
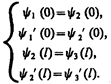 (221.6)
(221.6) (221.7)
(221.7)

 (222.1)
(222.1)



