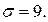Задание 3. Статистическая проверка статистических гипотез

 

ЗАКЛЮЧИТЕЛЬНОЕ ЗАНЯТИЕ

 

Содержание занятия.

I.2. Работа с методическим материалом.

Ликвидация задолженностей, отработка занятий по текущему разделу.

Подведение итогов обучения по предмету: выставление общего зачета, заполнение зачетных книжек и индивидуальных карт.

П Е Р Е Ч Е Н Ь

лабораторных и клинико-лабораторных навыков,

получаемых студентами на кафедре биохимии

 

1. Навыки лабораторной и экспериментальной работы:

 

- с агрессивно действующими веществами.

- очистки веществ методами осаждения, диализа.

- работы с мерной стеклянной посудой, микропипетками, микробюреткой.

- на фотоэлектроколориметре.

- титрометрическое количественное определение с помощью индикаторов.

- на центрифуге.

- проведения хроматографического разделения исследуемых образцов.

- разделения белковых смесей на фракции.

-знакомство с принципами экспериментальной научной работы.

- ведение протокола анализа.

- статистическая обработка цифрового материала по результатам исследования.

- с научной литературой. Реферативные работы по теме "Синтез белка и его регуляция".

 

2. Клинико-лабораторные навыки:

 

- количественное и качественное определение углеводов, применяемое в клинико-биохимических исследованиях.

- определение амилазной активности мочи.

- количественное определение показателей липидного обмена крови (холестерина, триацилглицеринов).

- количественное определение каталазы крови.

- навык обнаружение белка в биологической жидкости.

- количественное определение общего белка в биопробах.

- обнаружение витаминов и гормонов в растворах.

- количественное определение общей кислотности, свободной и связанной соляной кислоты желудочного сока.

- обнаружение молочной кислоты и крови в биопробах.

- выявление гомогентизиновой и фенилпировиноградной кислот в моче.

- определение креатинина, мочевой кислоты и мочевины.

- количественное определение желчных пигментов и гемоглобина.

- знакомство с методами экспресс-диагностики некоторых показателей крови и мочи.

Варианты заданий для контрольной работы

по дисциплине «Прикладная математика»

 

Задание 1. Выборка, её числовые характеристики

Для указанных ниже статистических распределений выборок требуется:

 

1) Найти эмпирическую функцию распределения и построить ее график.

2) Построить полигон частот.

3) Вычислить выборочную среднюю.

4) Вычислить выборочную и исправленную дисперсии.

 

Вариант 1. x_i1 4 8 10

n_i 5 3 2 1

Вариант 2. x_i-5 1 3 5

n_i 2 5 3 1

Вариант 3. x_i1 5 9 11

n_i 2 3 5 1

Вариант 4. x_i -2 1 2 3 4 5

n_i 2 1 2 2 2 1

Вариант 5. x_i0 1 2 3 4

n_i5 2 1 1 1

Вариант6. x_i1 5 6 8

n_i5 15 20 10

Вариант 7. x_i1 5 7 9

n_i6 12 1 1

 

Вариант 8. x_i 2 3 5 6

n_i 10 15 5 20

Вариант 9. x_i-5 2 3 4

n_i 4 3 1 2

Вариант 10. x_i1 2 4 7

n_i 1 3 6 2

Задание 2. Линейная корреляция

По данным, приведенным ниже, вычислить коэффициент корреляции, найти выборочное уравнение прямой линии регрессии Y на X, построить корреляционное поле и нанести на него прямую регрессии Y на X.

Вариант 1. X 5 9 10 12

Y 3 6 4 7

 

Вариант 2. X 1 2 5 8 16

Y 1,0 1,4 2,2 2,8 4,0

 

Вариант 3. X 1 3 4 7 10

Y -1,0 -2,1 -2,4 -3,0 -3,3

 

Вариант 4. X 2 5 7 10

Y 2 4 6 8

Вариант 5. X -1 -0,5 0 0,8 1,5

Y 2,7 3,2 4,0 6,5 11,0

 

Вариант 6. X -2 -1 0 1 2

Y 15,8 6,4 3,0 1,7 1,3

 

Вариант 7. X 1 3 6 8 10

Y 8,9 5,6 3,5 2,7 2,0

 

Вариант 8. X 1 3 6 10

Y 5,5 6,9 7,4 7,5

 

Вариант 9. X 9,5 10,5 11,0 12,0 14,5

Y 4,5 6,0 8,5 9,0 10,0

 

Вариант 10. X 6,6 7,0 8 9 9,8

Y 6,0 7,8 8,7 7,8 9

 

Задание 3. Статистическая проверка статистических гипотез

В вариантах 1–10 приведено эмпирическое распределение дискретной случайной величины X. Требуется, используя критерий , проверить на уровне значимости =0,05 гипотезу о распределении генеральной совокупности по закону Пуассона.

1. Случайная величина X – число вышедших из строя станков в цехе за одну смену. Число наблюдений n = 200:

x_i 0 1 2 3 4 5 6 7 8

n_i 41 62 45 22 16 8 4 2 0

2. Случайная величина X – число нестандартных коробок консервов в одном ящике. Число наблюдений n = 200:

x_i 0 1 2 3 4 5

n_i 132 43 20 3 2 0

3. Случайная величина X – число отказов радиоэлектронной аппаратуры. Число наблюдений n = 60:

x_i 0 1 2 3 4

n_i 42 11 4 3 0

4. Случайная величина X – число неправильных соединений в минуту на телефонной станции. Число наблюдений n = 60:

x_i 0 1 2 3 4 5 6 7 8

n_i 8 17 16 10 6 2 0 1 0

5. Случайная величина X – число деталей, поступивших на конвейер в течение 2-х минутного интервала. Число наблюдений n = 600:

x_i 0 1 2 3 4 5 6 7

n_i 400 167 29 3 0 0 1 0

6. Случайная величина X – число поврежденных стеклянных изделий в контейнере. Число наблюдений n = 500:

x_i 0 1 2 3 4 5 6 7 8

n_i 199 169 87 31 9 3 1 1 0

7. Cлучайная величина X – число сбоев в работе ЭВМ за неделю. Число наблюдений n = 20:

x_i 0 1 2 3 4 5

n_i 109 65 22 3 1 0

8. Случайная величина X – число заявок, поступающих на телефонную станцию в минуту. Число наблюдений n = 100:

x_i 0 1 2 3 4 5 6 7 8

n_i 7 21 26 21 13 7 3 2 0

9. Случайная величина X – число неправильно сброшюрованных учебников в партии. Число наблюдений n = 1000:

x_i 0 1 2 3 4 5 6

n_i 505 336 125 24 8 2 0

10. Случайная величина X – число заявок, поступающих в систему массового обслуживания в течение часа. Число наблюдений n = 100:

x_i 0 1 2 3 4 5 6 7 8 9 10 11

n_i 1 3 8 14 17 17 15 10 7 5 2 1

 

Задание 4. Доверительные интервалы для параметров нормального закона распределения

Найти доверительный интервал для оценки математического ожидания а нормального распределения с надежностью = 0,95, зная выборочную среднюю , объем выборки n и среднее квадратичное отклонение

Вариант 1. = 75,17; n = 36;

Вариант 2. = 75,16; n = 49;

Вариант 3. = 75,15; n = 64;

Вариант 4. = 75,14; n = 81;

Вариант 5. = 75,13; n = 100;

Вариант 6. = 75,12; n = 121;

Вариант 7. = 75,11; n = 144;

Вариант 8. = 75,10; n = 169;

Вариант 9. = 75,09; n = 196;

Вариант 10. = 75,08; n = 225;

Задание 5.

В группе n студентов. По контрольной работе n₁ студентов получили 5 баллов, n₂ студентов получили 4 балла, n₃ студентов получили 3 балла и n₄ студента получили 2 балла. Можно ли считать, что мы имеем дело с группой «троечников»?

1.1 n = 30, n₁ = 5, n₂ = 6, n₃ = 12, n₄ = 7.

1.2 n = 32, n₁ = 6, n₂ = 7, n₃ = 13, n₄ = 6.

1.3 n = 28, n₁ = 5, n₂ = 5, n₃ = 10, n₄ = 8.

1.4 n = 30, n₁ = 6, n₂ = 5, n₃ = 11, n₄ = 8.

1.5 n = 24, n₁ = 4, n₂ = 6, n₃ = 9, n₄ = 5.

1.6 n = 28, n₁ = 6, n₂ = 6, n₃ = 12, n₄ = 4.

1.7 n = 32, n₁ = 5, n₂ = 7, n₃ = 14, n₄ = 6.

1.8 n = 24, n₁ = 5, n₂ = 5, n₃ = 10, n₄ = 4.

1.9 n = 26, n₁ = 6, n₂ = 5, n₃ = 9, n₄ = 6.

1.10 n = 28, n₁ = 4, n₂ = 5, n₃ = 13, n₄ = 5.

Указание. Решить задачу с помощью критерия Пирсона.