Понятие эластичности. Эластичность спроса по цене. Коэффициенты эластичности спроса по цене. Факторы эластичности спроса по цене.
Логическая схема построения параграфа.
Эластичность характеризует реакцию одной переменной на изменение другой и исчисляется как отношение процентных изменений величин данных переменных. Прямая эластичность спроса по цене характеризует степень воздействия изменения цены на изменение объема спроса и исчисляется как отношение процентного изменения величины спроса на данный товар к процентному изменению его цены при прочих равных условиях: изменение Qd, в % изменение p, в % (6.1)
где Qd –объем спроса, p– цена товара, Edp - коэффициент эластичности спроса по цене. Коэффициент прямой эластичности спроса по цене (Edp) .показывает, на сколько процентов изменится объем спроса на товар при изменении его цены на 1%. Поскольку спрос и цена имеют обратную зависимость, то данный коэффициент всегда является величиной отрицательной. Однако, по причине того, что «минус» не имеет математического значения, а только характеризует разнонаправленность изменения спроса и цены, от него в дальнейшем мы будем абстрагироваться, используя модульное значение Edp. С точки зрения способа расчета различают точечную и дуговую эластичность спроса по цене. Точечная эластичность характеризует относительное изменение объема спроса при бесконечно малом изменении цены и определяется для каждой точки линии спроса по формуле:
DQd/ Qd 100% = DQd: Dp = DQd. p = dQd. p = Q′d(p). p D p/p 100% Qd p Dp Qd dp Qd Qd (6.2) где p и Qd - цена и объем спроса в данной точке линии спроса; Dp= dp – бесконечно малое изменение величины цены товара; DQd = dQd – изменение величины спроса; Q′d(p)-первая производная функции спроса от цены. Если функция спроса является линейной и задана уравнением типа Qd =a-bp, то линия спроса - прямая, ее наклон неизменен и равен коэффициенту b, b = DQd /Dp. Подставим данное выражение в формулу (6.2) и получим:
-b. P Qd (6.3)
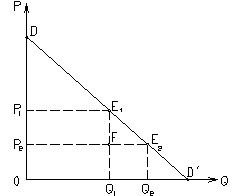
Как следует из формулы (6.3), эластичность спроса по цене в разных точкахпрямой, несмотря на ее одинаковый наклон, различна и определяется значениями P и Qd, а коэффициент эластичности Еdр может принимать любые значения в интервале от 0 (в т. А) до ¥ (в т. В) (рис.6.1). В верхней части линии спрос эластичен, поскольку цена относительно велика и ее процентное изменение незначительно, а величина спроса низка и ее процентное изменение достаточно велико. В ее нижней части имеет место обратная ситуация. Таким образом, все прямые линии спроса имеют различную эластичность в разных точках и по их наклону об эластичности судить нельзя (за исключением случаев с абсолютно эластичным или абсолютно неэластичным спросом, когда линии спроса параллельны осям координат – рис. 6.7 и 6.8).
Рис. 6.1 Различная эластичность спроса при неизменном наклоне линии спроса. Графически коэффициент точечной эластичности определяется соотношением отрезков линии спроса, лежащих ниже и выше интересующей нас точки. Таким образом, значение коэффициента Edp в точках Е1 и Е2 можно выразить следующим образом: Edp1=Е2 D¢/ DЕ2, в Edp2 =Е1 D¢/ DЕ1 (рис. 6.2).
Рис.6.2 Графическое определение коэффициента точечной эластичности для линейной функции спроса. Если функция спроса является нелинейной (линия спроса в данном случае будет кривой), то для графического определения коэффициента эластичности следует провести касательную к кривой спроса и продлить ее до пересечения с осью абсцисс и осью ординат. Значение точечной эластичности, по аналогии с предыдущим случаем, будет определяться соотношением отрезков данной касательной, лежащих ниже и выше интересующей нас точки. Так, например, значение коэффициента Edp в т. T (рис. 6.3) будет равно соотношению отрезков ТN и ТM, или Edp в т. T =ТN/ ТM.
Рис.6.3 Графическое определение коэффициента точечной эластичности для нелинейной функции спроса.
Дуговая эластичность или эластичность между двумя точками линии спроса определяется в случае значительных процентных изменений в цене или объеме спроса. Для ее расчета принято использовать метод средней точки интервала, предложенный английским экономистом Р.Алленом *. Данный метод основан на определении показателей средней величины исходного и последующего значений цены и спроса. Математическая формула расчета дуговой эластичности спроса на основе средней точки интервала выглядит следующим образом:
Еdp= DQd ×100%: Dp ×100% = (Qd2-Qd1): (р2-р1) = (Qd2-Qd1). (р1 + р2) (Qd1+Qd2)/2 (р1+р2)/2 (Qd1+Qd2) (р1+р2) (Qd1+Qd2) (р2-р1) (6.4) где р1 - цена до изменения; р2 -цена после изменения; Qd1 -величина спроса до изменения цены; Qd2 - величина спроса после изменения цены; Очевидно, что не всякое изменение цены отражается на величине спроса, и не всякое изменение спроса немедленно окажет влияние на цену. Гипотетически можно выделить пять вариантов или моделей реакции спроса на цену. 1.Спрос эластичен (1< |Edp| < ¥) Величина спроса активно реагирует на изменение цены, а ее уменьшение (P¯) вызывает такое увеличение спроса (Qd), что общая выручка растет (TR). И, наоборот: рост цены (P) вызывает такое уменьшение спроса (Qd¯), что общая выручка падает (TR¯). *В дальнейшем при расчете других коэффициентов эластичности мы будем использовать исключительно данный метод.
Рис.6.4. Эластичный спрос (1<|Edp|< ¥).
Как видно из графика (рис.6.4.), уменьшение цены на 1.5 доллара или на 66,6% привело к увеличению спроса на 4 единицы либо 133,3%, в результате чего выручка увеличилась с 3 до 7.5 долларов. Площадь прямоугольника PbPaAC иллюстрирует проигрыш от снижения цены, а площадь прямоугольника QaCBQb – выигрыш от увеличения спроса. Поскольку площадь QaCBQb больше площади PbPaAC, то снижение цены для продавца выгодно. 2.Спрос неэластичен (0<|Edp|<1). Величина спроса слабо реагирует на изменение цены и ее уменьшение (P¯) увеличивает его в такой степени (Qd), что потери от снижения цены не перекрываются выигрышем от роста спроса, и выручка уменьшается (TR¯). И, наоборот: увеличение цены (P) уменьшает объем спроса в такой незначительной степени (Qd¯), что выручка растет (TR).
Рис.6.5. Неэластичный спрос (0<|Edp|<1).
Из графика (6.5) видно, что уменьшение цены на 1,5 доллара или на 66,6% привело к увеличению спроса на 1 единицу или на 22,2%, в результате чего выручка уменьшилась с 12 до 7,5 долларов. Площадь прямоугольника PbPaAC, отражающая проигрыш от снижения цены, больше площади прямоугольника QaCBQb, отражающей выигрыш от увеличения спроса. Это означает, что увеличение объема продаж не способно компенсировать потери от уменьшения цены и ее снижение нецелесообразно. 3.Спрос с единичной эластичностью (|Edp|=1). Процентное изменение цены на товар вызывает абсолютно пропорциональное процентное изменение спроса, а уменьшение либо увеличение цены (P¯; P), соответственно, увеличивает либо уменьшает спрос (Qd; Qd¯) в такой степени, что потери от снижения цены равны выигрышу от роста спроса, и выручка остается неизменной (TR=const).
Рис.6.6. Спрос с единичной эластичностью (|Edp|=1).
Из графика (рис.6.6) видно, что уменьшение цены на 1,5 доллара или на 66,6% приводит к увеличению спроса на 1 единицу или на 66,6%, в результате чего выручка остается прежней и составляет 3доллара. Площадь прямоугольника PbPaAC равна площади прямоугольника QaCBQb. Это означает, что проигрыш от увеличения цены равен выигрышу от увеличения спроса и свидетельствует о том, что на рынке сложилась равновесная цена, которую изменять нецелесообразно, лучшим вариантом является сохранение сложившегося положения вещей. 4.Спрос абсолютно неэластичен (|Edp|=0). Данная модель является условной, поскольку иллюстрирует ситуацию, когда, независимо от цены, спрос всегда остается постоянным. Графически абсолютно неэластичный спрос представлен линией, параллельной оси ординат (рис.6.7).
Рис.6.7. Абсолютно неэластичный спрос (|Edp|=0). 5.Спрос абсолютно эластичен (|Edp|=¥). Данная модель также является условной, поскольку характеризует ситуацию, когда при данной цене может быть реализовано бесконечное количество товара, однако, при малейшем ее повышении спрос на товар становится равным нулю и не может быть продана ни одна его единица (рис.6.8).
Рис.6.8. Абсолютно эластичный спрос (|Edp|= ¥) Эластичность спроса по цене зависит ряда факторов: Во-первых, от наличия у данного товара субститутов и комплементов. Очевидно, что существование у некоторого товара заменителей делает спрос на него более эластичным, поскольку в случае повышения цены на него у потребителя есть выбор и реальная возможность заменить данный товар другим. Спрос на товары, не имеющие субститутов, практически всегда неэластичен, как, например, спрос на инсулин, без инъекций которого жизнь больных диабетом невозможна. Спрос на товар-комплемент, удельный вес затрат на приобретение которого составляет значительную часть бюджета потребителя, обычно является эластичным; спрос на товар-комплемент, удельный вес затрат на приобретение которого составляет незначительную часть потребительского бюджета, как правило, неэластичен. Например, спрос на бензин - эластичен, а на машинное масло – неэластичен.
В-третьих, от доли потребительского бюджета, отведенного на данный товар. Как правило, рост цен на товары, удельный вес расходов на которые в доходе потребителя незначителен, не оказывает существенного влияния на объем спроса на них и наоборот. Так, например, 20%-ное повышение цен на газеты вряд ли существенно уменьшит спрос на них. А вот 20%-ное повышение квартирной платы, вероятно, заставит квартиросъемщиков искать меньшие по площади квартиры. В-четвертых, от степени насыщения потребностей тем или иным благом: чем она выше, тем менее эластичен спрос на данный товар. Например, если семья состоит из трех человек и у каждого члена семьи имеется видеомагнитофон, то семья приобретет четвертую «видеодвойку», вероятно, только в случае существенного снижения цены. В-пятых, от разнообразия возможностей использования данного товара: чем разнообразнее эти возможности, тем более эластичен спрос на данный товар и наоборот. Так, например, спрос на универсальное оборудование будет более эластичным, чем спрос на специальное оборудование.
|