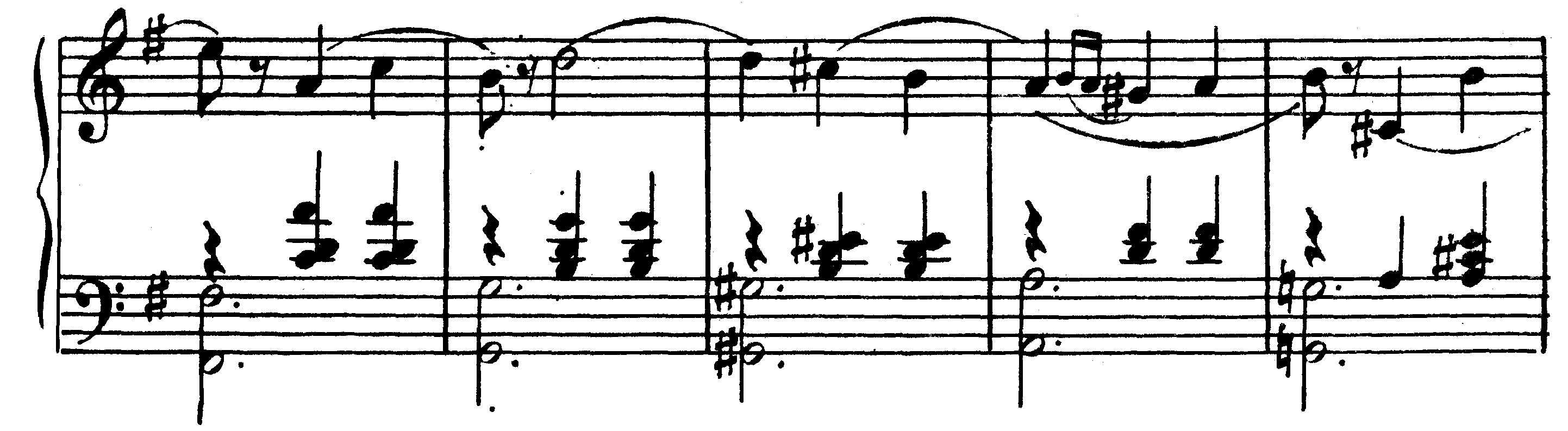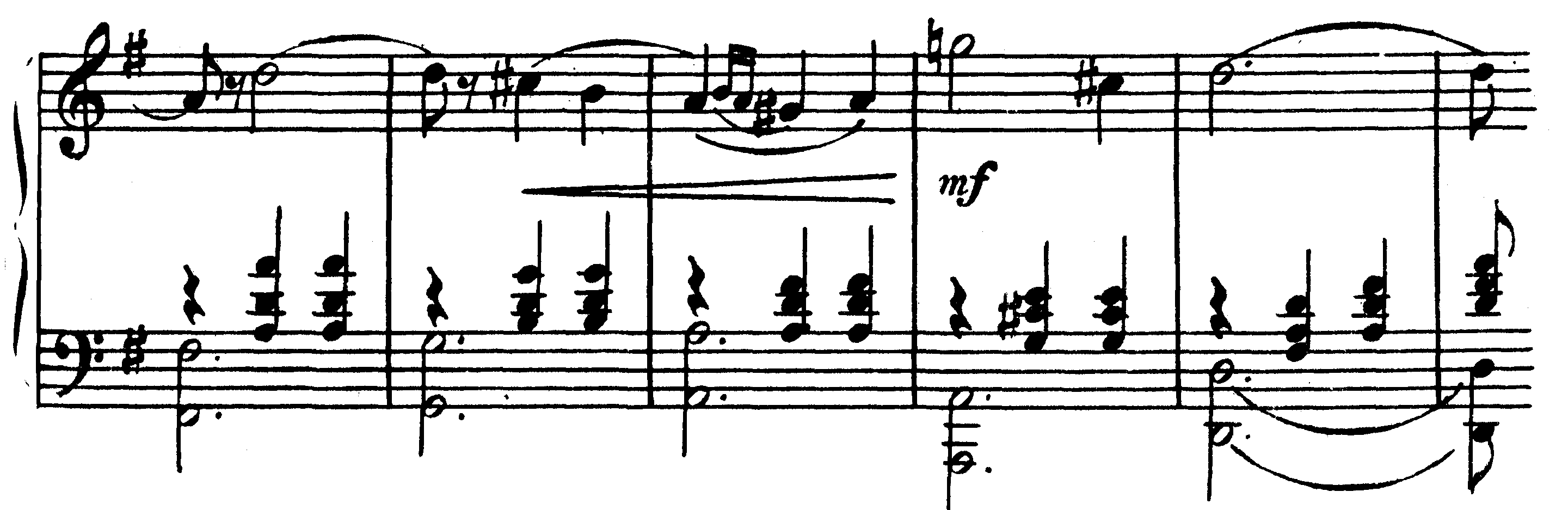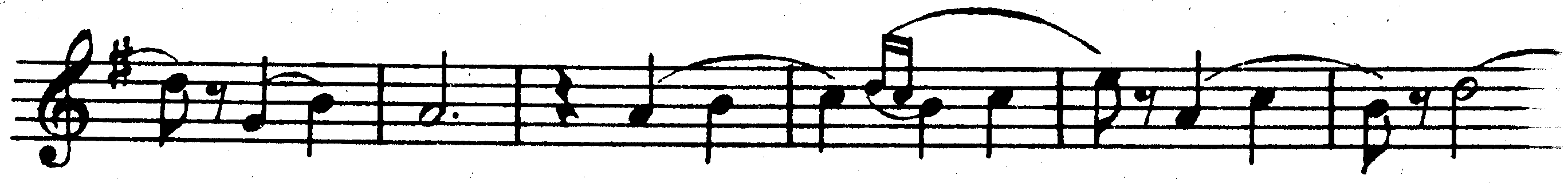Moderate. Tempo di Valse П. Чайковский. Серенада для струнного оркестра, ч. II

Частным случаем периода неповторного строения является неделимый на предложения период, называемый периодом единого развития.

Приведенные выше примеры отличаются не только тем, что первый из Них делится на два сходных по началу предложения, а второй на такие предложения не делится. Другое их отличие заключается в ладотональной стороне: пример из Гайдна заканчивается в той же тональности, что и начинается; пример же из Чайковского, начинающийся в G-dur, заканчивается в D-dur. По своему ладотональному содержанию периоды подразделяются на немодулирующие и модулирующие. Внутри немодулирующих периодов могут встретиться и иные тональности в виде гак называемых отклонений, но заканчиваются они всегда в исходной тональности.

В тех же примерах периодов есть и еще одно отличие: первый делится на два четырехтактных предложения, второй же может быть разделен на пять построений по 4 такта* [Затакт никогда не рассматривается как отдельный такт ввиду того, чтоальная доля, к которой он примыкает, находится в следующем такте.] Периоды, делящиеся на 2 четырехтакта, 2 восьмитакта, 2 шестнадцатитакта (а иногда и 2 тридцатидвухтакта), называются периодами квадратной структуры. Количество тактов в предложениях и в целом периоде в таких случаях представляет собой степень числа 2 (2²=4, 23=8, 2⁴=16 и т.д.). Периоды же, которые состоят из другого числа тактов, называются периодами неквадратной структуры. Неквадратный период, приведенный в примере 266, начинается с четырехтактного построения, за которым следует другой четырехтакт (то есть членится поначалу так, как это бывает в квадратных построениях). Однако в дальнейшем развитии не образуется шестнадцатитактного построения за счет так называемого расширения.

Расширением называется увеличение масштабов периода, происходящее внутри построения, то есть до заключительной каденции, приходящейся в данном примере на 18—20 такты. Чтобы уяснить себе роль расширения, достаточно представить данный период без него в виде, например, следующего построения:

267

Кроме расширения увеличение общего масштаба периода может произойти с помощью дополнения. В отличие от расширения дополнение следует после полной совершенной каденции (см., например, такты 15—22 первой темы медленной части симфонии № 5 Бетховена).