Principal concepts of the theory of errors
We can't define the true values of a physical quantity. We can define only the interval (x min, x max) of the investigated quantity with some probability a. For example: we can affirm, that students' height may be defined between 1.5 m and 2.0 m with probability of 0.9. Then we can prove, that students' height may be defined between 1.6 m and 1.8 m with smaller probability of 0.6 and so on. Value of this interval is called the entrusting interval. On fig.2.1 interval of quantity being investigated x is represented.
Figure 2.1
Where x is the most probable value of quantity being measured; Dx is the half width of the entrusting interval of the measured quantity with probability of a. Therefore we can estimate, that true value of the measured quantity may be defined as x = x or If a quantity x has been measured n times and x1, x2,..., xn are the results of the individual measurements then the most probable measured value or the arithmetic mean is:
The deviation
is called the mean accidental deviation of the measurements. Mean root square is defined as
where t – Student’s constant for definite a and n. The ratio of
is called the relative error of measurement and is usually expressed in percents:
|


 D x, with probability a,
D x, with probability a, .
. (2.1)
(2.1) is called the accidental error (deviation) of a single measurement.
is called the accidental error (deviation) of a single measurement.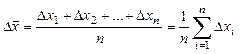 (2.2)
(2.2)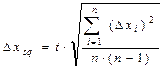 (2.3)
(2.3) (2.4)
(2.4)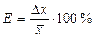 . (2.5)
. (2.5)


