Experimental part
1. Measure the diameter of the wire with the slide gauge and the length of the wire with a ruler. 2. Load the wire with 2÷3 weights to make it straight. 3. Fix the zero rotating the indicator scale. 4. Measure the lengthening of the wire Δ l gradually loading it with the weights. Force F applied to the wire equals the sum of weights being loaded to the wire. Put down the results of the measurements m, F, Δ l in a table 6.2. The length of the wire and its diameter are l = 1100 mm, d = 0,6 mm. Calculate mechanical stress and relative deformation according to formula 6.3 and 6.4. Put down the results in table 6.2.
Table 6.2
5. Plot the dependency of σ = f(ε) accordingly to fig. 6.4, i.e. draw the best straight line lying in the maximum density of experimental points. Choose any of two points 1 and 2 (but not from the table) to which values of
Figure 6.4
6. Calculate modulus of Yung by the formula:
Having such a method of determining the coefficient of proportionality (fig.6.4) between any values that laniary are related one to another, the all the totality of experimental data but not accidental value of any measurement is used. Using the data from table 6.1 determine the material of the wire. 7. Using the theory of errors estimate relative error of measurement Modulus of Yung by the formula:
where the value δl calculate according to the formula:
where δ = 0.01 mm;
6. On the base of relation σ = f(ε) make the conclusion if the Hook Law is true.
|
, 
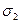and 
, 
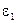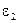accordingly.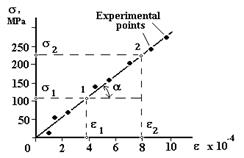
(6.6)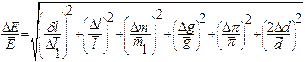
, (6.7)
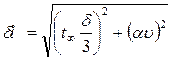, (6.8)
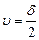. According to the formula:
(6.9) calculate the values: Dl (
), Dm (
), Dg (
), Dp (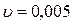
), Dd (
).
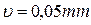