Выполнение измерений. Измерения удлинения проводят для одной из двух пружин (по указанию преподавателя), для чего на подвеску помещают грузы различной массы
Измерения удлинения проводят для одной из двух пружин (по указанию преподавателя), для чего на подвеску помещают грузы различной массы. Сначала с помощью закреплённой вертикально линейки измеряют длину пружины с пустой подвеской – l 0. Затем на подвеску кладут самый большой груз из полученного набора, измеряют длину l (см. рис. 4.1). Массы грузов в граммах указаны прямо на них. Затем на первый груз помещают любой другой груз, снова замеряют длину и т.д., до 5 грузов. Общую массу грузов на подвеске и результаты измерений длины заносят в табл. 4.1, где l 0 – координата подвески без груза, l – с грузом. (Подумайте, нужно ли здесь учитывать массу подвески). Таблица 4.1
Задание 2. Определение коэффициента упругости пружины динамическим методом Этот метод основан на законах колебательного движения груза массой m около положения равновесия. Основной признак колебательного движения – периодичность. Следовательно, смещение x груза из положения равновесия можно записать в виде периодической функции времени:
где A – амплитуда; w = 2p /T – циклическая частота, обратно пропорциональная периоду T колебаний; j0 – начальная фаза колебаний. При смещении x величина силы упругости будет определяться полным удлинением пружины, равным сумме D l и x (см. рис. 4.1):
Записав второй закон Ньютона (4.1) в проекциях на ось x и учтя выражения (4.4) и (4.6), нетрудно получить дифференциальное уравнение свободных колебаний подвешенного на пружине тела:
где После подстановки значений
Зная циклическую частоту колебаний w и колеблющуюся массу m, можно определить значение коэффициента упругости
Из последнего равенства видно, что период определяется только свойствами системы (m и k) и не зависит от амплитуды колебаний. Уравнение (4.9) позволяет графически обработать результаты измерений периода: откладывая по осям соответствующие переменные, можно свести равенство (4.9) к виду y = c + bx и получить при построении графика прямую, по угловому коэффициенту которой можно найти коэффициент упругости k. Подумайте, что следует принять за y, за х, за b,чтобы свести уравнение (4.9) к указанной линейной зависимости.
|

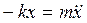 ,
,
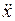
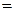 ax – проекция ускорения груза на ось х.
ax – проекция ускорения груза на ось х.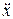 и x в уравнение (4.7) получим
и x в уравнение (4.7) получим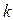 . Так как непосредственно измеряется время, то лучше связать коэффициент упругости не с частотой, а с периодом колебаний. Нетрудно показать, что квадрат периода колебаний груза на пружине прямо пропорционален его массе и обратно пропорционален коэффициенту упругости пружины:
. Так как непосредственно измеряется время, то лучше связать коэффициент упругости не с частотой, а с периодом колебаний. Нетрудно показать, что квадрат периода колебаний груза на пружине прямо пропорционален его массе и обратно пропорционален коэффициенту упругости пружины: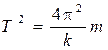 .
.



