Теория метода и описание установки
Одним из экспериментальных методов определения моментов инерции тел является метод крутильных колебаний. Этим методом можно определить момент инерции любого тела, имеющего не только правильную, но и неправильную форму, момент инерции которого рассчитать трудно (зубчатое колесо с отверстиями, отливка и др.).
где Если пренебречь силами трения, то из основного закона динамики вращения (см. выражение (2.5) в лабораторной работе № 2) будем иметь
где I – момент инерции висящего на проволоке тела относительно оси крутильных колебаний. Так как величина возвращающего момента сил прямо пропорциональна смещению j от положения равновесия, то возникающие крутильные колебания будут гармоническими и угол поворота j(t)будет периодической функцией времени:
где j m – амплитуда колебаний, т.е. максимальное значение угла поворота j; w – циклическая частота колебаний, связанная с периодом T соотношением
a0 – начальная фаза колебаний. Угловое ускорение тела, как известно, может быть определено как вторая производная от угла поворота по времени:
Произведя двойное дифференцирование выражения (3.3) и подставив значения j и e в (3.2), можно получить связь между угловой частотой крутильных колебаний тела и коэффициентом упругости подвеса:
Заменив в этом уравнении w через период колебаний T и измерив его, можно определить момент инерции подвешенного тела, если известен коэффициент упругости k:
Если же значение коэффициента упругости проволоки неизвестно, то его можно исключить, написав аналогичное уравнение для другого тела – правильной формы, момент инерции I 0которого легко рассчитать:
Здесь k имеет то же значение, что и в выражении (3.6), если тело с неизвестным моментом инерции I подвешено на том же подвесе. Приравнивая правые части выражений (3.6) и (3.8), легко получить уравнение, дающее возможность найти момент инерции тела любой формы по рассчитанному значению I 0 и двум периодам колебаний T 0 и T, которые определяются измерениями. В качестве тела с известным моментом инерции в нашей работе взято кольцо, момент инерции которого рассчитывается по его массе т и размерам:
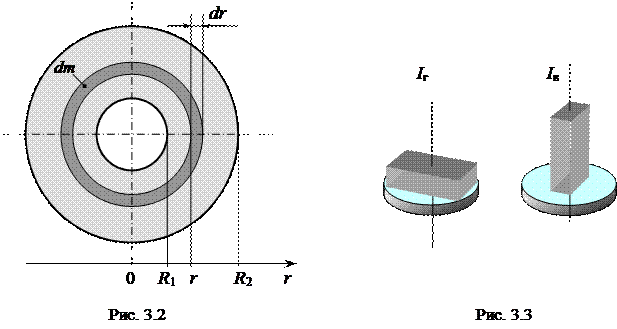
где R 1 – внутренний радиус, а R 2 – внешний радиус кольца. Расчётное значение момента инерции кольца (3.9) получено интегрированием выражения, которое определяет момент инерции сплошного тела
В случае кольца элемент массы dm выбирается в виде бесконечно тонкого колечка произвольного радиуса r (рис. 3.2), и интегрирование ведётся в пределах от R 1 до R 2. Масса элемента dm прямо пропорциональна объёму dV колечка и плотности r материала, из которого изготовлено кольцо:
где b – толщина кольца. Подставляя в (3.10) это выражение, получаем
После несложных преобразований, выделив здесь массу кольца как произведение его объёма на плотность, получим формулу (3.9).
Установка для проведения измерений представляет собой стойку с кронштейном, на котором закреплена стальная проволока длиной около метра. К нижнему концу проволоки прикреплена лёгкая платформа, моментом инерции которой пренебрегаем, так как он очень мал по сравнению с инертностью эталонных колец и исследуемого тела. На платформе симметрично относительно оси проволоки могут размещаться либо тело произвольной формы, либо кольца разных размеров. Для фиксации положения тела в симметричном положении по проволоке можно перемещать лёгкую пробку. В основание стойки ввёрнуто три винта, с помощью которых стойка устанавливается вертикально – так, чтобы проволока с подвешенным к ней грузом была параллельна стойке.
|

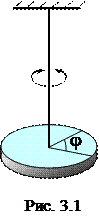 Крутильные колебания возникают, если тело, подвешенное на упругой проволоке (рис. 3.1), повернуть на некоторый угол j и отпустить. В проволоке появляются упругие силы, направленные в сторону, противоположную углу поворота. Возникает момент сил, пропорциональный углу поворота и стремящийся вернуть тело в положение равновесия:
Крутильные колебания возникают, если тело, подвешенное на упругой проволоке (рис. 3.1), повернуть на некоторый угол j и отпустить. В проволоке появляются упругие силы, направленные в сторону, противоположную углу поворота. Возникает момент сил, пропорциональный углу поворота и стремящийся вернуть тело в положение равновесия: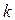 – коэффициент упругости подвеса.
– коэффициент упругости подвеса.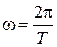 ;
;
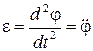 .
.
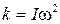 .
.
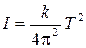 .
.
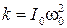 .
.
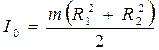 ,
,
 .
.
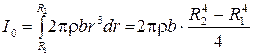 .
.