Теория метода и описание установки. Для описания вращательного движения твёрдого тела используют кинематические и динамические характеристики
Для описания вращательного движения твёрдого тела используют кинематические и динамические характеристики, перечисленные в табл. 2.1. Таблица 2.1
В табл. 2.1 m – масса; dm – бесконечно малый элемент массы; r – расстояние от оси вращения; Динамические характеристики имеют следующий физический смысл: I – мера инертности при вращательном движении (аналог массы);
Все векторы, характеризующие вращательное движение, направлены по оси вращения в соответствии с «правилом буравчика». Линейная скорость точки, находящейся на расстоянии r от оси вращения (точнее – модуль скорости
Тангенциальное ускорение
Нормальное ускорение
Основной закон динамики вращательного движения тела (аналог II закона Ньютона)
где
При опускании груза сила натяжения нити приводит во вращение крестовину. На стержнях крестовины с помощью винтов на равных расстояниях от оси вращения укрепляют четыре одинаковых груза, размеры которых малы по сравнению с их расстоянием от оси вращения. Во время движениякрестовина вращается под действием момента
где R – плечо силы В рассматриваемом случае на крестовину действует не только сила натяжения нити, но и различные силы трения-сопротивления. Поэтому основной закон динамики вращательного движения (2.5) должен включать в себя и момент сил трения, т.е.
Величину вращающего момента легко найти, зная силу натяжения нити и радиус шкива, на который наматывается нить. Из второго закона Ньютона для груза m, опускающегося с ускорением а (см. рис. 2.1), и из выражения (2.6) получаем
Ускорение a груза одновременно является тангенциальным ускорением at точек вращающегося шкива, поэтому угловое ускорение крестовины
Ускорение груза и, следовательно, угловое ускорение можно найти экспериментально. Но в уравнении движения (2.7) остаются две неизвестные величины: момент сил трения M три момент инерции крестовины I, так что однозначное решение его при неизменном значении массы груза m невозможно. Однако графически найти и момент инерции, и момент сил трения нетрудно. Для этого следует записать уравнение (2.7) в проекции на ось вращения и привести к известному виду линейной функции y = c + bx. По графику этой функции легко найти постоянные c и b. В нашем случае это будет уравнение
Проведя измерения с разными массами и построив по данным измерений график зависимости M нот e, можно найти по нему обе искомые величины: момент инерции I и обобщённый момент сил сопротивления движению M тр. Подумайте, как это сделать!
|

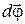 – угловое перемещение;
– угловое перемещение;
 – угловая скорость;
– угловая скорость;
 – угловое ускорение
– угловое ускорение
 ;
;
 – момент силы;
М = F×l – модуль момента силы, Нм;
– момент силы;
М = F×l – модуль момента силы, Нм;
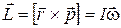 – момент импульса, кгм2/с
– момент импульса, кгм2/с
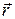 – радиус-вектор точки приложения силы;
– радиус-вектор точки приложения силы; 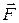 – сила; F – модуль силы; l – плечо силы;
– сила; F – модуль силы; l – плечо силы; 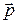 – импульс материальной точки.
– импульс материальной точки.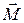 – мера действия при вращательном движении (аналог силы);
– мера действия при вращательном движении (аналог силы); – мера количества движения при вращении (аналог импульса тела).
– мера количества движения при вращении (аналог импульса тела). )
)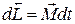 ,
,
 – сумма моментов сил, действующих на тело. Для тела с постоянным моментом инерции
– сумма моментов сил, действующих на тело. Для тела с постоянным моментом инерции .
.
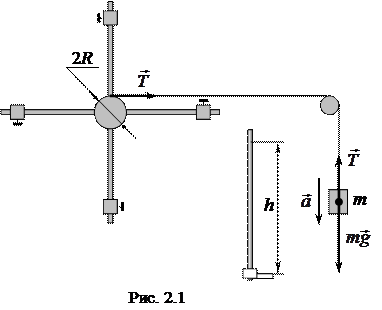 Маятник Обербека, с помощью которого исследуется зависимость между величинами, входящими в выражение основного закона динамики вращательного движения, представляет собой крестовину (рис. 2.1), вращающуюся вокруг горизонтальной оси. На шкив крестовины наматывается нить, к концу которой прикреплён груз массой m.
Маятник Обербека, с помощью которого исследуется зависимость между величинами, входящими в выражение основного закона динамики вращательного движения, представляет собой крестовину (рис. 2.1), вращающуюся вокруг горизонтальной оси. На шкив крестовины наматывается нить, к концу которой прикреплён груз массой m. силы натяжения нити
силы натяжения нити 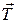 . Модуль момента силы натяжения
. Модуль момента силы натяжения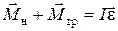 .
.
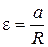 .
.



