Теория метода и описание установки. При движении тела в жидкости или газе на него действует сила сопротивления , зависящая от скорости тела
При движении тела в жидкости или газе на него действует сила сопротивления При малых скоростях жидкость плавно обтекает тело, не создавая разности давлений, и сила сопротивления практически равна силе трения между слоями жидкости, движущимися с различными скоростями: Ньютон показал, что величина силы внутреннего трения между слоями жидкости пропорциональна площади S соприкосновения слоёв и градиенту скорости d u /dx, который показывает, насколько убывает скорость слоёв жидкости при перемещении на единицу длины в перпендикулярном к скорости направлении x:
где r – плотность жидкости. Шарик радиусом R, падающий в жидкости, обволакивается ею, и вместе с прилегающим к его поверхности слоем движется со скоростью u (рис. 7.1). Прилипший слой приводит в движение соседние слои жидкости, скорость которых постепенно уменьшается по мере удаления от оси движения шарика (профиль скоростей показан на рис. 7.1 штриховой линией). Г. Стокс установил, что при малых скоростях и размерах шарика (ламинарное течение) скорость слоёв жидкости становится равной нулю на расстоянии L = 2 R/ 3 от поверхности шарика. Точнее, это имеет место при малых значениях безразмерного критерия Рейнольдса
где D – диаметр шарика; u – его скорость. Следовательно, если выполняется условие ламинарности течения Re << 1, то градиент скорости
Поскольку площадь поверхности шарика S = 4p R 2, то модуль силы сопротивления при Re < 0,1
и сила Архимеда
В выражениях (7.6) и (7.7) g – ускорение свободного падения, r1 – плотность шарика, r2 – плотность жидкости. Если начальная скорость шарика равна нулю, то F c = 0 и шарик вначале будет двигаться ускоренно. Но по мере увеличения скорости шарика будет возрастать и сила сопротивления, и наступит такой момент, когда сумма приложенных к шарику сил станет равной нулю:
и дальнейшее движение шарика будет равномерным со скоростью u = uравн. Записывая второй закон Ньютона (7.8) в проекции на направление скорости и используя выражения (7.5), (7.6), (7.7), можно получить расчётную формулу для определения коэффициента динамической вязкости:
Таким образом, чтобы вычислить значение коэффициента динамической вязкости, нужно измерить диаметр шарика и определить скорость его равномерного движения Установка для определения вязкости методом Стокса представляет собой вертикально расположенный стеклянный цилиндр с исследуемой жидкостью, куда и опускается шарик известного радиуса R. На боковой поверхности цилиндра имеется шкала, по которой измеряют путь l, пройденный шариком. Время, затраченное на прохождение отрезка пути, измеряется секундомером. Для улучшения условий наблюдения цилиндр подсвечивается лампой дневного света.
|

 , зависящая от скорости тела. В общем случае сила сопротивления имеет две составляющие – силу трения F т и силу давления F д. Сила трения обусловлена вязкостью жидкости, и пропорциональна скорости u тела. Сила давления определяется разностью давлений на передней и задней поверхностях тела, её величина пропорциональна квадрату скорости u2.
, зависящая от скорости тела. В общем случае сила сопротивления имеет две составляющие – силу трения F т и силу давления F д. Сила трения обусловлена вязкостью жидкости, и пропорциональна скорости u тела. Сила давления определяется разностью давлений на передней и задней поверхностях тела, её величина пропорциональна квадрату скорости u2. .
. .
.
 Здесь h – коэффициент пропорциональности, характеризующий вязкость жидкости и называемый коэффициентом динамической вязкости. Также вязкость жидкости может быть охарактеризована коэффициентом кинематической вязкости
Здесь h – коэффициент пропорциональности, характеризующий вязкость жидкости и называемый коэффициентом динамической вязкости. Также вязкость жидкости может быть охарактеризована коэффициентом кинематической вязкости ,
,
 ,
,
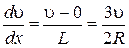 .
.
 Кроме силы сопротивления, на шарик, падающий в жидкости, действуют также сила тяжести (рис. 7.2)
Кроме силы сопротивления, на шарик, падающий в жидкости, действуют также сила тяжести (рис. 7.2)
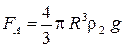 .
.
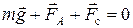 ,
,
 .
.



