КИНЕМАТИКА МАТЕРИАЛЬНОЙ ТОЧКИ
3 МЕХАНИЧЕСКОЕ ДВИЖЕНИЕ 1. Предметом механики является изучение закономерностей простейшей формы движения материи – механического движения. Механическим движением называется процесс изменения взаимного расположения тел или их частей в пространстве с течением времени. В определении отражен тот факт, что механическое движение (перемещение), как и всякое другое движение, происходит в пространстве и времени. Пространство и время – сложные философские категории, несмотря на их кажущуюся очевидность, основанную на нашем житейском опыте. Эти понятия в ходе развития физики и философии претерпели весьма существенные изменения. И.Ньютон, создавая свою механику, постулировал, что пространство и время имеют абсолютный характер. Что это значит? Это значит, что пространство и время существует независимо от материи и движения. Пространство, по Ньютону, - протяженное, неподвижное, пустое вместилище материальных тел. Оно однородно (в нём нет привилегированных точек, все его точки равноправны), изотропно (в нём нет привилегированных направлений, все его направления равноправны) и эвклидово (его геометрия описывается геометрией Эвклида). Время, по Ньютону, - абсолютная длительность, не зависящая от тел. Оно также однородно (в нем нельзя найти мгновение, которое отличалось бы от других) и всюду во Вселенной течет равномерно и одинаково. Механика, постулирующая абсолютный характер пространства и времени, называется ньютоновской или классической. Успехи классической механики в 17-19 в.в. были столь поразительны, что, по словам немецкого физика М.Лауэ, она стала «наукой, стоящей над опытом», т.е. наукой, положения которой не нуждаются в опытной проверке. В начале 20 века некоторые представления классической механики подверглись кардинальному пересмотру. Этот пересмотр привел к созданию одной из величайших научных теорий нашего времени – теории относительности. Основные идеи теории относительности, созданной А.Эйнштейном, сводятся к тому, что пространство и время неотделимы от материи и ее движения и имеют относительный, а не абсолютный характер, что свойства пространства и времени зависят от конкретных материальных тел, от характера и интенсивности их движений. Теория относительности установила, что классическая механика с ее представлениями об абсолютном пространстве и едином времени имеет ограниченный, приближенный характер. Она с достаточной степенью точности описывает лишь медленные (по сравнению со скоростью света) движения макроскопических тел и совершенно непригодна для описания быстрых движений и движений микрообъектов. Быстрые движения макроскопических тел описывает так называемая релятивистская механика или специальная (частная) теория относительности. Движения микрочастиц рассматривает механика, называемая квантовой. Необходимо отметить, что ни теория относительности, ни квантовая механика не отвергают полностью классическую механику, они развивают ее дальше на принципиально новой основе, обобщая на случай сколь угодно больших скоростей и сколь угодно малых масс. В пределе уравнения релятивистской и квантовой механики (в первом случае при Следовательно, современная физика рассматривает механику Ньютона как частный, предельный случай релятивистской механики, с одной стороны, и квантовой – с другой. 2. Понятие «механического движения» неприменимо к одному, отдельному телу. О движении данного тела имеет смысл говорить лишь тогда, когда есть возможность определить его положение относительно другого тела или других тел. Поэтому, приступая к изучению движения какого – либо тела, мы должны сначала установить, по отношению к какому телу будем рассматривать движение. Из соображений удобства это тело условно считается «неподвижным». Тело, которое условно считается неподвижным, по отношению к которому определяется положение других тел, называется телом отсчёта или системой отсчёта. 3. Механическое движение можно рассматривать с разных точек зрения. Во-первых, с геометрической, т.е. изучать внешнюю сторону различных видов движения, не вникая в те взаимодействия и причины, которые обусловливают тот или иной вид движения. Во-вторых, с причинно-следственной, т.е. изучать движение с точки зрения тех взаимодействий, которые обусловливают данное движение или изменяют его. Разделы механики, изучающие движение с указанных точек зрения, называются соответственно кинематикой и динамикой. Особо рассматриваются условия равновесия (статика). 4. В рамках кинематики выбор системы отсчёта ничем не ограничен, все системы равноправны и любая из них может использоваться при описании движения. С точки зрения динамики некоторые системы отсчёта имеют преимущество перед другими. Вопрос о том, какими должны быть эти преимущественные системы, будет рассмотрен позднее. 5. Основными объектами механики является материальная точка и абсолютно твёрдое тело. Материальная точка – это тело, формой и размерами которого в данной задаче можно пренебречь. Вопрос о том, можно ли данное тело считать материальной точкой, определяется не абсолютными размерами этого тела, а условиями задачи, масштабами движения. Одно и тоже тело в разных задачах может рассматриваться и как материальная точка, и как протяженное тело. Например, при определении траектории полёта искусственного спутника Земли его с успехом можно принимать за материальную точку, но при расчёте затрат энергии на преодоления сопротивления атмосферы при выведении спутника на орбиту его следует считать телом, имеющим определённую форму, размеры и т.д. Абсолютно твёрдое тело это тело, деформациями которого в условиях данной задачи можно пренебречь. В таком теле расстояния между отдельными точками остаются неизменными. Изучение законов механического движения естественно начать с движения материальной точки. Движение такого объекта – простейшее движение, ибо в этом случае не приходится учитывать вращение тела и смещение отдельных его частей. 6. Что значит знать движение материальной точки? Это значит знать её положение в пространстве в любой момент времени. Для определения положения точки в пространстве и аналитического описание её движения с выбранным телом отсчёта необходимо связать какую-либо координатную систему. Выберем прямоугольную (декартову) систему координат. Тогда положение материальной точки M будет однозначно определено, если будут заданы координаты x, y, z (рис.1).
Так как для определения положения материальной точки необходимо задать три координаты, то говорят, что материальная точка имеет три степени свободы. Вместо трёх скалярных величин x, y, z положение точки может быть задано одной векторной – радиус-вектором ус-вектора на координатные оси: Радиус-вектор связан со своими проекциями следующим соотношением: где Модуль вектора (его абсолютная величина):
4 ЛИНЕЙНЫЕ КИНЕМАТИЧЕСКИЕ ХАРАКТЕРИСТИКИ ДВИЖЕНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ
1. Если материальная точка движется, то это означает, что ее положение относительно выбранной системы отсчёта, т.е. ее координаты с течением времени изменяются. Найти кинематический закон движения точки – значит найти конкретный вид функции, выражающей зависимость координаты от времени:
x=f1 (t); y=f2(t); z=f3 (t). (4.1) Если из этих уравнений исключить время, то мы получим уравнение траектории движения. 2. Траекторией движения материальной точки называется линия, которую эта точка описывает при своем движении. В зависимости от формы траектории различают движения прямолинейные и криволинейные (частным случаем криволинейного движения является движение по окружности). Форма траектории зависит от системы отсчёта, относительно которой рассматривается движение. 3. Пусть материальная точка в данной системе отсчёта двигалась по некоторой криволинейной траектории (рис. 2). В момент времени t1 она занимала положение A, определяемое радиус-вектора Вектор Легко видно из чертежа, что перемещение Отрезок траектории
4. Одно и то же перемещение Для характеристики быстроты изменения пространственного положения движущихся тел вводится понятие линейной скорости. Линейная скорость Следует в общем случае различать среднюю и истинную или мгновенную скорости. Пусть материальная точка, двигаясь по произвольной траектории, за некоторый промежуток переместилась на времени, надо средней скоростью Направление вектора средней скорости совпадает с направлением пе-
Вектор
Но Следовательно, мгновенная скорость равна производной от радиус-вектора движущейся точки по времени:
Численное значение (модуль) мгновенной скорости:
5. Поскольку проекциями радиус-вектора
Модуль мгновенной скорости равен
Зная проекции вектора скорости на оси координат, можно найти и сам вектор 6. Радиус-вектор 7. В процессе движения величина и направление скорости могут изменяться. Быстроту изменения линейной скорости с течением времени характеризует линейное ускорение. Линейное ускорение - векторная физическая величина, характеризующая процесс изменения линейной скорости с течением времени, численно равная изменению скорости за единицу времени и совпадающая по направлению с направлением этого изменения. По аналогии со средней и мгновенной скоростью введем среднее и мгновенное ускорения. Пусть в некоторый момент времени t1, точка двигалась со скоростью На чертеже векторную разность найдем следующим образом. Перенесем вектор Разделив Направление вектора
Используя обозначение производной, выражение (4.9) можно переписать:
т.е. ускорение в любой момент времени определяется производной от скорости по времени. Направление мгновенного ускорения совпадает с направлением приращения скорости Так как т.е. ускорение равно второй производной от радиус-вектора 8. Проекции вектора ускорения выражаются производными от соответствующих компонент скорости по времени:
Принимая во внимание, что
получим: т.е. проекции вектора ускорения на координатные оси выражаются вторыми производными от соответствующих координат по времени. Модуль ускорения равен Сам вектор 9. Вектор ускорения характеризует изменение величины и направления скорости. Эти изменения можно оценивать раздельно. Разложим вектор приращения скорости на две составляющие следующим образом. Из точки А (рис.5), в которой совмещены начала векторов
Вектор
Разделим обе части выражения (4.16) на
В пределе, т.е. при Предел отношения Предел отношения Можно показать, что численное значение тангенциального ускорения равно производной от величины скорости по времени, а численное значение нормального ускорения прямо пропорционально квадрату скорости и обратно пропорционально радиусу кривизны траектории в данной точке:
Таким образом, тангенциальное ускорение Нормальное ускорение Предел отношения
Таким образом, тангенциальное и нормальное ускорения представляют собой две взаимно перпендикулярные составляющие полного ускорения:
Так как
10. Проанализируем некоторые частные случаи движения. а) аτ=0; ап=0 - равномерное прямолинейное движение; б) аτ=const; ап=0 - равнопеременное (равнозамедленное или равноускоренное) прямолинейное движение; в) аτ=0; ап=const - равномерное движение по окружности; г) аτ=0; ап= f(t) - равномерное криволинейное движение; д) аτ= f(t); ап = f(t) - неравномерное криволинейное движение. 11. В заключение отметим, что поскольку нормальное ускорение всегда направлено к центру кривизны, а тангенциальное - по каса
5 ОСНОВНАЯ ЗАДАЧА КИНЕМАТИКИ
1. Основная задача кинематики – нахождение положения движущейся точки, ее скорости и ускорения в любой интересующий момент времени. Пусть известен вид функций, выражающих зависимость координат движущейся точки от времени: x=f1 (t); y=f2(t); z=f3 (t) (5.1) Чтобы найти положение точки в некоторый момент t = t1, достаточно это время подставить в (5.1). Исключив из (5.1) время, находят траекторию движения. Чтобы найти зависимость от времени компонент скорости надо продифференцировать по времени функции (5.1). Зная компоненты Двукратным дифференцированием функций (5.1) мы получим зависимость от времени компонент ускорения. 2. Возможна обратная задача: по функциям, выражающим зависимость компонент ускорения от времени, можно найти величину и направление скорости, а также координаты точки в заданный момент времени. Эта задача решается обратной операцией - интегрированием: однократное интегрирование дает зависимость от времени компонент скорости, двукратное - зависимость от времени координат. При этом в формулах появляются постоянные интегрирования. Эти постоянные определяются из так называемых начальных условий. Начальные условия - это параметры механического состояния в некоторый определенней момент времени (обычно этот момент относят к началу отсчета времени t = 0, отсюда и название – начальные условия). Начальные условия должны быть заданы дополнительно, в противном случае задача становится неопределенной.
Пусть даны графики зависимости координат от времени. Проанализируем один из них, изображенный на рис.7. Из приведенного графика легко определить проекции средней и истинной скорости на ось ОХ. Проекция средней скорости за промежуток времени
Геометрически Проекция истинной скорости на ось ОХ в момент времени t численно равна тангенсу угла наклона касательной (2), проведенной к графику в точке а: 4. Определив несколько значений Тангенсы углов наклона секущей и касательной на этом графике определят проекции среднего и истинного ускорений на ось ОХ, т.е. (аср)х и ах . 5. Графически можно решать и интегральные задачи. Так, например, по графику ускорения можно найти изменения скорости за данный промежуток времени, по графику скорости – изменение координаты
(т.е. расстояние, пройденное вдоль соответствующей оси). Ри Узкая полоска на рис. 8 изображает элементарное изменение (приращения) компоненты скорости d Изменения этого компонента за конечный промежуток времени
Совершенно аналогично изменения координаты В заключение отметим, что графическое интегрирование может быть выполнено значительно точнее, чем графическое дифференцирование. ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Пример 1. Уравнение движения точки по прямой имеет вид:
Найти: 1) положения точки в моменты времени 3) мгновенные скорости в указанные моменты времени; 4) среднее ускорение за указанный промежуток времени; 5) мгновенные ускорения в указанные моменты времени.
Решение. 1) Положение точки определяется значениями расстояния
2) Значение средней скорости по определению
3) Общее выражение для мгновенной скорости по определению имеет вид Подставив в это выражение вместо
4) Значение среднего ускорения определим как
ни
5) Общее выражение для мгновенного ускорения имеет вид
Подставив в это выражение вместо
Пример 2. Определить зависимость пути от времени, если ускорение тела пропорционально квадрату скорости и направлено в сторону, противоположную ей. Решение. Учитывая, что по условию ускорение пропорционально квадрату скорости и противоположно ей, запишем это в виде
Произведем разделение переменных После интегрирования имеем Выразим Пример 3. Зависимость пути, пройденного точкой по окружности радиусом Решение. Прежде всего находим выражение для скорости точки. Известно, что
Теперь найдем общее выражение для тангенциального ускорения. Из теории известно, что Полученное выражение для тангенциального ускорения не содержит времени; это значит, что оно постоянно по величине и движение точки по окружности будет равнопеременным. Нормальное (центростремительное) ускорение найдем по его формуле Полное ускорение будет равно геометрической сумме взаимно перпендикулярных тангенциального и нормального ускорений
ВОПРОСЫ ДЛИ САМОПРОВЕРКИ
1. Дайте определение механического движения. 2. Что называется системой отсчета? 3. Что называется материальной точкой? 4. Как задается положение материальной точки в пространстве? 5. Что называется перемещением? путем? 6. Раскройте физический смысл мгновенной скорости и ускорения. 7. Какие изменения скорости характеризуют тангенциальное и нормальное ускорения? Как находят численные значения этих ускорений? 8. Может ли точка, движущаяся по криволинейной траектории, не иметь тангенциального ускорения? Может ли эта точка не иметь нормального ускорения? 9. Как по графику x = f(t) найти составляющую скорости
|


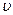 << C, С – скорость света в вакууме, во втором при
<< C, С – скорость света в вакууме, во втором при 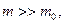
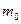 - масса электрона) переходят в уравнения классической механики.
- масса электрона) переходят в уравнения классической механики.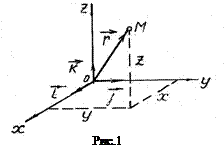 Число независимых координат, которые необходимо задать, чтобы однозначно определить положение материального объекта (точки, системы точек, тела и т.д.) в пространстве, называется числом степеней свободы.
Число независимых координат, которые необходимо задать, чтобы однозначно определить положение материального объекта (точки, системы точек, тела и т.д.) в пространстве, называется числом степеней свободы.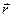 , проведенным из начала координат в точку, в которой находится частица (рис.1). Координаты x, y, z являются проекциями ради-
, проведенным из начала координат в точку, в которой находится частица (рис.1). Координаты x, y, z являются проекциями ради- (3.1)
(3.1)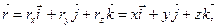 (3.2)
(3.2)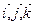 – единичные векторы вдоль координатных осей x,y,z.
– единичные векторы вдоль координатных осей x,y,z.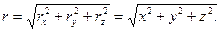 (3.3)
(3.3)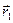 , в момент времени t2 - положение B, определяемое радиус-вектора
, в момент времени t2 - положение B, определяемое радиус-вектора 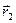 .
.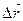 , проведенный из начальной точки А в конечную В, называется линейным перемещением за время
, проведенный из начальной точки А в конечную В, называется линейным перемещением за время 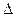 t = t2 – t1.
t = t2 – t1.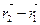 .
.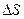 , заключенный между точками А и В, называется путем, пройденным за тот же промежуток времени
, заключенный между точками А и В, называется путем, пройденным за тот же промежуток времени 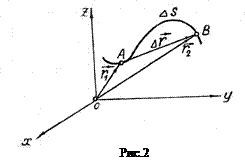 Численные значения
Численные значения 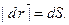
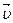 – это векторная физическая величина, характеризующая процесс изменения пространственного положения движущейся точки относительно выбранной системы отсчёта, численно равная линейному перемещению, совершенному за единицу времени, и совпадающая по направлению с направлением этого перемещения.
– это векторная физическая величина, характеризующая процесс изменения пространственного положения движущейся точки относительно выбранной системы отсчёта, численно равная линейному перемещению, совершенному за единицу времени, и совпадающая по направлению с направлением этого перемещения.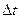 :
: 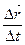 . Эта величина называется
. Эта величина называется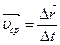 . (4.2)
. (4.2)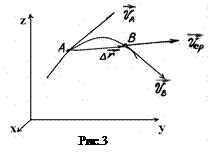 ремещения
ремещения  будет совпадать с направлением касательной. При
будет совпадать с направлением касательной. При 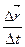 стремится к вполне определенному пределу.
стремится к вполне определенному пределу.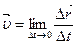 (4.3)
(4.3)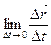 есть производная от
есть производная от 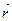 по t:
по t: 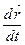
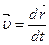 (4.4)
(4.4)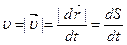
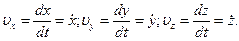 (4.5)
(4.5)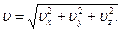 (4.6)
(4.6)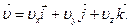 (4.7)
(4.7)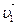 , а в момент t2 - со скоростью
, а в момент t2 - со скоростью 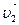 . Изменение скорости за промежуток времени
. Изменение скорости за промежуток времени 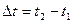 очевидно, равно
очевидно, равно 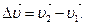
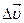 , соединяющий конец
, соединяющий конец 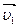 с концом
с концом 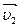 и будет представлять собой изменение (или приращение) скорости за время
и будет представлять собой изменение (или приращение) скорости за время 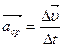 . (4.8)
. (4.8)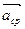 , как это видно из формулы (4.8), совпадает с направлением вектора
, как это видно из формулы (4.8), совпадает с направлением вектора 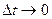 отношение
отношение 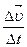 стремится к вполне определенному пределу
стремится к вполне определенному пределу 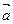 , называемому истинным или мгновенным ускорением (ускорением в данный момент времени):
, называемому истинным или мгновенным ускорением (ускорением в данный момент времени):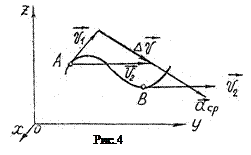
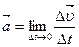 (4.9)
(4.9)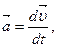 (4.10)
(4.10)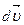 за бесконечно малый промежуток времени и в зависимости от характера изменения величины и направления скорости может составлять с вектором скорости любой угол. Этот угол будет острым, если величина скорости возрастает (в частности, он может быть равен нулю, если скорость, возрастает по величине, но не меняется по направлению). Если величина скорости уменьшается, (замедленное движение), то этот угол будет тупым (в случае, если скорость уменьшается по величине, оставаясь неизменной по направлению, он равен π). Наконец, если скорость изменяется только по направлению, вектор ускорения в любой точке траектории перпендикулярен к ней (траектория в этом случае - окружность).
за бесконечно малый промежуток времени и в зависимости от характера изменения величины и направления скорости может составлять с вектором скорости любой угол. Этот угол будет острым, если величина скорости возрастает (в частности, он может быть равен нулю, если скорость, возрастает по величине, но не меняется по направлению). Если величина скорости уменьшается, (замедленное движение), то этот угол будет тупым (в случае, если скорость уменьшается по величине, оставаясь неизменной по направлению, он равен π). Наконец, если скорость изменяется только по направлению, вектор ускорения в любой точке траектории перпендикулярен к ней (траектория в этом случае - окружность).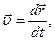 то
то 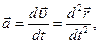 (4.11)
(4.11)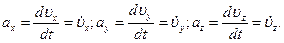 (4.12)
(4.12)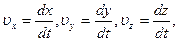
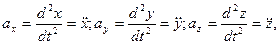 (4.13)
(4.13)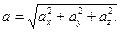 (4.14)
(4.14)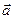 равен
равен 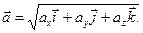 (4.15)
(4.15)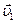 и
и 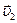 вдоль линии вектора
вдоль линии вектора 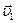 Тогда, как видно из чертежа, вектор
Тогда, как видно из чертежа, вектор 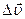 можно представить как геометрическую сумму двух векторов -
можно представить как геометрическую сумму двух векторов - 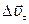 и
и 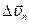 :
: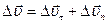 (4.16)
(4.16)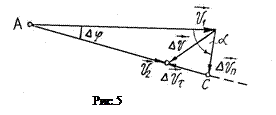 Обозначим углы, которые образуют линии векторов
Обозначим углы, которые образуют линии векторов 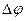 и
и 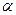 .
.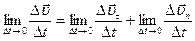 (4.17)
(4.17)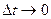 , угол
, угол 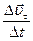 при
при 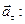
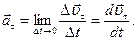 (4.18)
(4.18)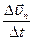 при
при 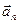 :
: 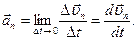 (4.19)
(4.19)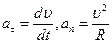 (4.20)
(4.20)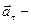 вектор, характеризующий изменение скорости по величине, направленный по касательной к траектории и численно равный
вектор, характеризующий изменение скорости по величине, направленный по касательной к траектории и численно равный 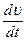 .
.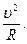
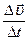 при
при 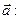
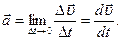 (4.21)
(4.21) (4.22)
(4.22)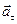 и
и 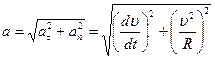 . (4.23)
. (4.23)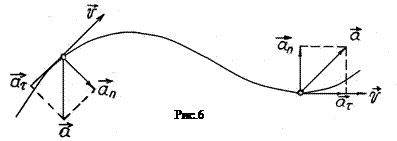 тельной к траектории, то полное ускорение всегда обращено внутрь траектории (рис.6)
тельной к траектории, то полное ускорение всегда обращено внутрь траектории (рис.6)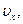
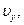
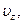 легко определить величину и направление самой скорости.
легко определить величину и направление самой скорости.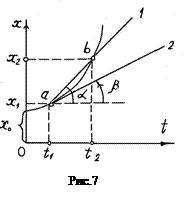 3. Основная задача кинематики может быть решена графически.
3. Основная задача кинематики может быть решена графически.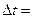 t2 – t1 равна
t2 – t1 равна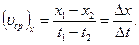
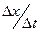 есть тангенс угла наклона секущей (1), проведенной через точки
есть тангенс угла наклона секущей (1), проведенной через точки  и
и 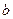 . Следовательно,
. Следовательно, 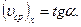 (5.2) Обратим внимание на то, что при нахождении угла наклона секущей отрезки
(5.2) Обратим внимание на то, что при нахождении угла наклона секущей отрезки 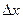 и
и 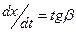 (5.3)
(5.3)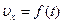 .
.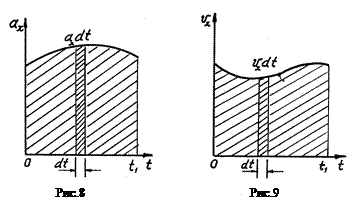 сунки 8 и 9 поясняют это.
сунки 8 и 9 поясняют это.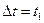 будет численно равно площади криволинейной трапеции, покрытой на чертеже редкой штриховкой:
будет численно равно площади криволинейной трапеции, покрытой на чертеже редкой штриховкой: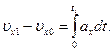 (5.5)
(5.5)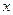 за время
за время 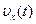 на участке 0 - t1 (рис.9):
на участке 0 - t1 (рис.9): 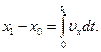 (5.6)
(5.6)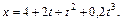
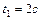 и
и 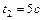 ; 2) среднюю скорость за время, протекшее между этими моментами;
; 2) среднюю скорость за время, протекшее между этими моментами;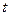 значения заданных моментов времени
значения заданных моментов времени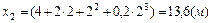
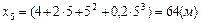
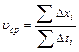 или
или  , где
, где 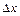 - изменение расстояния
- изменение расстояния 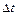 :
: ,
,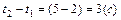 ,
,
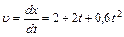
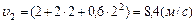 ,
,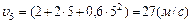 .
.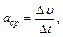 где
где 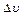 - изменение скорости
- изменение скорости 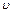 за промежуток време-
за промежуток време-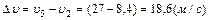
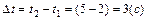

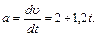
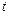 его заданные значения, получим
его заданные значения, получим 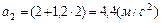 ,
,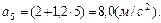
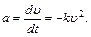
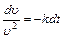 и проинтегрируем.
и проинтегрируем.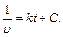 При
При 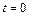
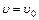 , значит,
, значит, 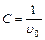 и
и 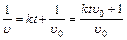 ; Откуда
; Откуда 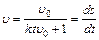 .
.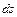 :
: 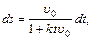 тогда
тогда 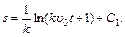 При
При 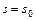 , значит,
, значит, 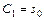 . Окончательно будем иметь
. Окончательно будем иметь 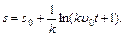
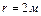 , от времени выражено уравнением
, от времени выражено уравнением 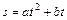 . Найти скорость, нормальное, тангенциальное и полное ускорение точки через
. Найти скорость, нормальное, тангенциальное и полное ускорение точки через 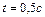 после начала движения, если
после начала движения, если 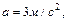
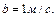
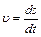 . Взяв производную по времени от заданного уравнения пути
. Взяв производную по времени от заданного уравнения пути  , получим
, получим 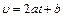 . Значение скорости в данный момент времени найдем, если в полученную формулу подставим время
. Значение скорости в данный момент времени найдем, если в полученную формулу подставим время 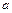 и
и 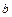 :
: .
.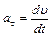 . Взяв производную по времени от уравнения скорости, находим
. Взяв производную по времени от уравнения скорости, находим 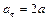 . С учетом коэффициента
. С учетом коэффициента 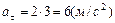 .
.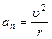 , подставив выражение для скорости, а затем, и численные их значения:
, подставив выражение для скорости, а затем, и численные их значения: 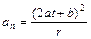 ;
; 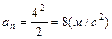 .
.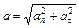 ;
;