ДИНАМИКА МАТЕРИАЛЬНОЙ ТОЧКИ
Кинематика изучает лишь пространственно-временные соотношения. В ее уравнениях отсутствуют величины, характеризующие свойства материальных тел, например, масса и их взаимодействие друг с другом, например, сила, импульс силы и др. Зависимость характера движения от свойств тел и от их взаимодействия друг с другом устанавливает динамика. Изучение динамики начнем с динамики материальной точки. 6 ПОНЯТИЕ СИЛЫ Рассмотрим физическое содержание одного из важнейших механических понятий - понятия силы. 1. Опыт показывает, что изменение физических свойств материальных объектов происходит только в процессе внешних или внутренних взаимодействий. Одной из форм взаимодействия является механическое воздействие. Механическое воздействие, оказываемое одним телом на другое, проявляется либо в изменении размеров и формы тела, либо в измене-нии скорости, либо в том и другом одновременно. Воздействуя, например, на балку, мы вызываем ее изгиб, отталкивая от берега лодку, мы заставляем ее двигаться, изменять скорость и т.д. Понятие силы служит для обозначения величины и направления механического воздействия одного тела на другое. Сила - это векторная физическая величина, характеризующая механическое воздействие одного тела на другое, в результате которого тела деформируются или приобретают ускорения. 2. Как видно из определения, понятие силы в механике значительно уже нашего житейского представления о ней. Мы говорим, например, о мускульном усилии, о «силе» болевого ощущения, о «силе воли» и т.д. Между тем, эти понятия никакого отношения к физическому понятию «сила» не имеют. Заметим, что даже в самой физике есть термины, связанные со словом «сила», но содержание которых не имеет отношения к понятию «сила» (например, электродвижущая сила, сила света, оптическая сила и т.д.) 3. Сила - величина векторная. Как и всякая другая векторная величина, сила характеризуется не только численным значением, но и направлением в пространстве (направлением действия). Кроме того, в большинстве случаев о векторе силы можно говорить как о связанном векторе и характеризовать точкой приложения. Если действие силы проявляется только в деформациях, его называют статическим. Если действие силы вызывает изменение скорости, его называют динамическим. Так как и деформации, и ускорения доступны количественному измерению, то любое из этих проявлений может быть использовано для сравнения и измерения сил. 4. Конкретные силы, рассматриваемые физикой, достаточно разнообразны: сила тяжести, вес, реакции опор, силы сухого и вязкого трения, силы упругие, поверхностные, межмолекулярные, реактивная сила и т.д. Однако по своей природе все они могут быть сведены к одной из так называемых фундаментальных сил. Фундаментальные силы - это силы, характеризующие основные типы взаимодействия между материальными объектами. В настоящее время известны гравитационное, электромагнитное, ядерное или сильное и слабое взаимодействия. Гравитационное взаимодействие характеризуют гравитационные силы, электромагнитное - электромагнитные, ядерное – ядерные. Слабое взаимодействие, имеющее место, например, при Гравитационные силы действуют между любыми материальными частицами и зависят от массы частиц и расстояния между ними. Электромагнитные силы действуют между заряженными частицами и зависят от величины электрического заряда частиц, их взаимного расположения и относительной скорости движения. Электромагнитные силы принято делить на электрические (обусловлены положением заряженных частиц) и магнитные (обусловлены движением заряженных частиц). Наконец, ядерные силы действуют между нуклонами - частицами, образующими атомное ядро. Особенностью ядерных сил является их необычайная интенсивность и короткий радиус действия (порядка 10-15м). Действие одного материального тела на другое, по представлениям современной физики, передается с конечной скоростью через посредство особой непрерывной материи, называемой физическим полем. В соответствии с типами взаимодействия известны гравитационное, электромагнитное и ядерное поля.
7 ПОНЯТИЕ СВОБОДНОГО ТЕЛА И ИНЕРЦИАЛЬНОЙ СИСТЕМЫ ОТСЧЕТА. 1. Как уже указывалось, в динамике существенную роль играет выбор системы отсчета. Физические явления протекают, вообще говоря, по-разному в разных системах отсчета. Естественно поэтому выбирать такие системы, в которых однотипные явления, например, механические, протекают одинаково и выглядят наиболее просто. Чтобы физические явления выглядели наиболее просто, систему отсчета следует связывать с так называемым свободным телом. Свободное (свободно движущееся) тело - это тело, не взаимодействующее с другими телами, тело, предоставленное самому себе. Система отсчета, связанная со свободно движущимся телом, называется инерциальной. Понятия свободного тела и инерциальной системы отсчета являются абстракциями. Опыт показывает, что в природе нет таких тел, которые бы так или иначе не взаимодействовали друг с другом, были бы абсолютно свободными. Поэтому, строго говоря, свободных тел, а значит, и инер-циальных систем отсчета не существует. Но существует бесчисленное множество реальных систем, которые со сколь угодно большой степенью точности приближаются к инерциальной системе. Например, системы, связанные с определенными звездами, будут весьма близки к инерциальным. В меньшей степени инерциальной будет система, связанная с Землей (эта система не является инерциальной потому, что она испытывает ускорение, обусловленное суточным вращением Земли вокруг своей оси и годичным движением вокруг Солнца). Однако для целого ряда физических экспериментов можно пренебречь неинерциальностью «земной» системы, поскольку вносимые при этом ошибки достаточно малы. Мысленных инерциальных систем существует бесчисленное множество. Все системы, связанные со свободными телами, инерциальны. 8 ПЕРВЫЙ ЗАКОН НЬЮТОНА В основе динамики лежат три закона И. Ньютона (1642-1727), сформулированные им в «Математических началах натуральной философии» (1687 г.). Все три закона сформулированы для инерциальной системны отсчета. 1. В первом законе речь идет о движении свободного тела. Физическое содержание первого закона динамики было раскрыто Г. Галилеем (1564 - 1642) задолго до того, как Ньютон дал его формулировку. До Галилея еще со времен Аристотеля (ІV век до н.э.) в физике господствовало убеждение, что равномерное прямолинейное движение поддерживается силой. В «Метафизике» Аристотеля мы читаем: «Движущееся тело останавливается, как только сила, его толкающая, прекращает свое действие». Телам приписывалось некое внутреннее стремление останавливаться. Галилей был первым, кто решительно отверг эти ошибочные представления. Он пришел к выводу, что в реальных условиях «стремление» тел останавливаться обусловлено не их внутренними свойствами, а вторичными, внешними причинами. Галилей понял, что в реальных условиях сила необходима не для того, чтобы поддерживать равномерное прямолинейное движение, а для того, чтобы компенсировать уже имеющееся внешнее воздействие, прежде всего силу трения, которая обычно является основной причиной прекращения движения. Галилей на опыте убедился, что если силу трения постепенно уменьшать (до известных пределов этого можно добиться техническими средствами - обработкой поверхностей скольжения, подбором подходящих материалов, смазкой и т.д.), то движение, т.е. скорость тела, будет изменяться все медленнее и медленнее. Идя дальше по этому пути уже мысленно, абстрагируясь от реальных условий, Галилей пришел к выводу, что в отсутствие внешних воздействий движение тела должно сохраняться неизменным сколь угодно долго, т.е. всякое свободное тело должно двигаться равномерно и прямолинейно (или покоиться). Движение, которое тело совершает в отсутствие внешнего воздействия, называется инерциальным, а сам принцип инерциального движения - законом инерции. Инерциальное движение происходит само по себе, оно является неотъемлемым, естественным состоянием любого освобожденного от внешнего воздействия материального тела и вовсе не нуждается в каких-либо внешних «двигателях». Напротив, неинерциальное движение (движение неравномерное, ускоренное) всегда происходит только при наличии непрерывного внешнего воздействия. Неинерциальное движение тотчас же переходит в инерциальное, как только исчезает воздействие сил. Это значит, что если в момент прекращения действия сил тело покоилось, то оно и в последующем будет пребывать в этом состоянии, если же тело двигалось, то в дальнейшем оно будет сохранять величину и направление той скорости, какую имело в момент исчезновения сил. Таким образом, первый закон динамики утверждает, что в инерциальной системе отсчета всякое свободное тело сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока внешнее воздействие не заставит его изменить это состояние. 2. Все, о чем говорилось выше, требует известного напряжения абстрактной мысли. Дело в том, что непосредственно на опыте мы не можем ни доказать, ни опровергнуть первый закон динамики. Инерциальное движение - это идеальный, предельный случай движения. 3. В реальных условиях мы можем практически полностью скомпенсировать внешние воздействия и наблюдать почти равномерное прямолинейное движение. Так, компенсируя силу трения, действующую на поезд, тягой электровоза, мы можем заставить его двигаться практически равномерно и прямолинейно. Значит, в реальных условиях, тело покоится или движется равномерно и прямолинейно, если векторная сумма всех действующих на него сил равна нулю: или кратко
4. Первый закон Ньютона справедлив только в инерциальной системе отсчета. Это нетрудно понять. Представим две системы, движущиеся друг относительно друга с ускорением. Пусть тело, свободное от воздействия, движется относительно одной из систем равномерно и прямолинейно, Так как вторая система движется относительно первой с ускорением, то и тело относительно этой, второй, системы будет двигаться с ускорением. Чтобы в отсутствии внешнего воздействия тело двигалось равномерно и прямолинейно, необходимо, чтобы свободной от воздействия была сама система отсчета. Такую систему мы условились называть инерциальной. Так как первый закон динамики выполняется только в инерциальных системах отсчета, то само определение инерциальной (или неинерциальной) системы можно дать с точки зрения выполнения этого закона. Инерциальная система отсчета - это система, в которой первый закон Ньютона - закон инерции выполняется абсолютно точно. Иначе говоря, это такая система, относительно которой свободное тело движется равномерно и прямолинейно. 5. Первый закон Ньютона в механике играет весьма важную роль и имеет вполне самостоятельное значение, а не является простым следствием второго закона, как это может, на первый взгляд показаться. В этом законе содержится постулат о существовании инерциальных систем отсчета, идея об однородности и изотропности пространства относительно инерциальных систем отсчета. Если тело свободно от внешних воздействий, то ничто не может изменить его скорость относительно таких систем. Пространство, будучи однородным и изотропным, само по себе изменить эту скорость не может.
9 ВТОРОЙ ЗАКОН НЬЮТОНА
1. Второй закон Ньютона отвечает на вопрос, каким будет движение тела относительно инерциальной системы отсчета при наличии сил. Этот закон утверждает: тело под действием силы приобретает ускорение, пропорциональное этой силе. Несмотря на то, что второй закон динамики является обобщением опытных фактов, проверить его со всей строгостью непосредственно на опыте, в реальных земных условиях невозможно. На опыте этот закон оправдывается лишь приближенно. Почему? Во-первых, потому, что во всех таких опытах неизбежно присутствуют дополнительные воздействия (трение, сопротивление среды и т.д.), учесть которые оказывается далеко не просто. Во-вторых, потому, что опыты проводятся на Земле - в неинерциальной системе отсчета, в системе, которая сама движется с ускорением. Результатом этого является то, что наблюдаемые ускорения не вполне соответствуют реально действующим силам. Наблюдаемые ускорения обусловлены не только воздействием сил, но и неинерциальностью системы отсчета. Однако если предпринять меры к тому, чтобы ускорения, обусловленные силами, были значительно больше ускорений, обусловленных неинерциальностью системы отсчета, то экспериментальная точность опытов будет вполне удовлетворительной. 2. Будем воздействовать на одно и то же тело разными силами и всякий раз находить отношение силы к соответствующему ускорению -
Можно убедиться в том, что отношение силы к сообщаемому ею ускорению постоянно для любых других тел (при этом величина его может оказаться разной). Мы приходим к выводу, что отношение Свойство тел изменять величину и направление скорости постепенно называется инерцией. Можно сказать, таким образом, что масса есть количественная мера инерции материальных тел. Чем больше масса тела, тем меньшее ускорение оно приобретает под действием данной силы, т.е. тем медленнее изменяется его скорость. Масса тела не зависит от температуры тела, его агрегатного состояния, химического состава, электрических, магнитных, упругих и иных свойств. В классической механике масса полагается величиной аддитивной (масса составного тела равна сумме масс отдельных его частей и не зависящей от скорости движения). Содержание массы, однако, не исчерпывается одними только динамическими проявлениями. В ряде физических явлений масса служит мерой иных свойств материальных объектов. Поэтому часто массу, фигурирующую во втором законе Ньютона и характеризующую инерционные свойства тел, называют «инертной». 3. Соотношение (9.1) позволяет по динамическому эффекту, обусловленному силой,- ускорению, найти массу тела. Мы будем, однако, полагать, что масса измерена каким-либо другим способом (это возможно). Тогда соотношение (9.1) можно толковать как зависимость ускорения не только от силы, но и от массы:
k - коэффициент пропорциональности, зависящий от выбора единиц измерения ускорения, силы и массы. Эти единицы выбирают таким образом, чтобы k = 1. Тогда Опыт показывает, что направление ускорения всегда совпадает с направлением силы, вызвавшей это ускорение. Учитывая направления Это – одна из простейших формулировок второго закона Ньютона. Ускорение, приобретаемое телом относительно инерциальной системы отсчета, прямо пропорционально силе, действующей на тело, зависит от массы тела и направлено в сторону силы. 4. Формулу (9.4) можно записать в виде
Это соотношение используется в качестве определяющего уравнения при установлении единиц измерения силы. В системе СИ масса измеряется в килограммах (сокращенно кг), ускорение – в метрах на секунду за секунду (
Силу часто измеряют в килограммах (кГ). Килограмм – это такая сила, которая телу массой 1кг сообщает ускорение 9,8
5. Чтобы перейти от векторной формы записи второго закона к скалярной, векторные величины соотношения (9.5) следует спроектировать на координатные оси выбранной системы координат: тах = Fx; таy = Fу; (9.6) таz = Fz; 6. Опыт показывает, что при взаимодействии материальных тел выполняется принцип независимости действия сил (принцип суперпозиций): если на тело одновременно действует несколько сил, то действие каждой силы происходит независимо от других. Это значит, что деформация или ускорение, обусловленные данной силой, будут тако-выми, как если бы других сил не было. Следовательно, в общем случае, когда на тело одновременно действуют несколько сил, под
т.е. ускорение, приобретенное телом, прямо пропорционально результирующей всех действующих на тело сил и обратно пропорционально его массе. 7. Приведем теперь более общую формулировку второго закона Ньютона. Механическое движение в процессе взаимодействия тел может быть частично или полностью передано от одного тела к другому. Чтобы судить о потенциальных возможностях какого-либо тела в этом отношении, недостаточно знать одну только скорость перемещения – в этом нас убеждает опыт. Сравните, например, движения футбольного мяча, летящего со скоростью 20 м/с, и поезда, идущего со скоростью 20 м/с; «запасы» механического движения этих тел различны, несмотря на одинаковую скорость. По-видимому, должна существовать единая мера механического движения, одинаковая для всех тел. Такая мера действительно существует и называется импульсом или количеством движения. Импульс - это векторная физическая величина, характеризующая способность механического движения передаваться от одного тела к другому, численно равная произведению массы тела на его скорость и совпадающая по направлению с направлением скорости:
Заметим, что численное значение импульса и его направление зависят от выбора системы отсчета, так как от системы отсчета зависит величина и направление скорости. Опыт показывает, что изменение импульса тела однозначно связано с величиной и направлением силы, которая на него действует. Пусть в некоторый момент времени t импульс тела был Ньютон установил, что скорость изменения импульса тела (произ-водная от импульса по времени), равна по величине действующей силе и совпадает с ней по направлению:
Это соотношение и есть общая форма математической записи второго закона Ньютона. Из этой формулы можно получить тот частный вид математического выражения второго закона, который мы привели выше. Действительно, если масса не изменяется с течением времени, то ее можно вынести за знак производной:
8. Создавая свою механику, Ньютон не подозревал, что масса, так же как и пространство, и время, - понятие относительное, зависящее от системы отсчета, от скорости движения. Поэтому предположение о неизменности массы без каких-либо специальных оговорок молчаливо положено в основу классической механики. С точки зрения ньютоновской механики выражение второго закона динамики
С точки зрения современной физики эти формулы равноправны только для медленных (по сравнению со скоростью света) движений, когда изменением массы, обусловленным изменением скорости тела, можно пренебречь. При скоростях, соизмеримых со скоростью света, эффект возрастания массы будет столь ощутим, что формула (9.5) оказывается непригодной. Для быстрых движений необходимо пользоваться формулой (9.9). Дифференцируя левую часть этого уравнения по правилам дифференцирования сложной функции, получим:
9. Соотношение (9.9) позволяет сделать вывод о том, что сила характеризует процесс передачи механического движения от одного тела к другому и численно равна импульсу, передаваемому за единицу времени. 10. Математическое выражение второго закона часто приводят еще в одном виде. Умножим обе части уравнения (9.9) на
Величина Импульс силы – это вектор, численно равный произведению силы на время ее действия и совпадающий по направлению с направлением силы. В левой части соотношения (9.11) стоит изменение импульса тела за элементарный промежуток времени 11. Из формулы (9.11) видно, что второй закон Ньютона – закон дифференциальный. Его можно привести к интегральному виду. Обозначим импульс буквой
Сложим все элементарные приращения импульса за конечный промежуток времени
Если Если 12. Обратимся к более подробному рассмотрению понятия инерции. Инерция - важнейшее свойство, присущее всем материальным объектам (в том числе и полевой форме материи). Этим свойством тела обладают независимо от того, свободны они или взаимодействуют с другими телами, покоятся или движутся. Необходимо чётко представлять, в чем проявляется инерция тел в различных условиях: в отсутствии внешнего воздействия и при наличии такового. Ответ на этот вопрос дают первый и второй законы Ньютона. В отсутствие внешнего воздействия инерция проявляется в том, что тело сохраняет неизменным свое состояние движения или покоя. При наличии внешнего воздействия – сил, инерция проявляется не в том, что тело стремится сохранить свое состояние движения неизменным (ибо как только нескомпенсированая, даже сколь угодно малая сила начинает действовать, движение тела - величина и направление скорости - тотчас же изменяются, возникает ускорение), а в том, что изменения движения тела происходит постепенно. Следовательно, инерция - это свойство тела сохранять имеющееся состояние движения или покоя (относительно инерциальной системы отсчета) неизменным при отсутствии воздействия и изменять это состояние постепенно при наличии воздействия. С проявлениями инерции мы сталкиваемся очень часто. Но, к сожалению, объяснения этих проявлений иногда бывают ошибочными. Поэтому мы рассмотрим здесь один пример. Пусть на гладком, без бортиков столике движущегося вагона лежит предмет. При резком торможении поезда этот предмет может соскользнуть со столика. Почему? Потому, отвечают некоторые, «что предмет сохраняет свою первоначальную скорость», «продолжает двигаться по инерции». Такое объяснение, в сущности, ошибочно. В самом деле, почему столик изменяет свою скорость, а предмет ее сохраняет? Могут ответить: «на столик действует тормозящая сила со стороны вагона (столик жестко скреплен с вагоном). Это верно, но разве на предмет не действует тормозящая сила? Действует! Тормозящей силой для предмета является сила трения, приложенная к нему со стороны столика (при торможении поезда эта сила направлена в сторону, противоположную движению). Так как на предмет действует неуравновешенная сила, скорость его (относительно полотна дороги) не может сохраняться, она изменяется! Вся суть в том, что изменение скорости столика и предмета происходят неодинаково быстро, иными словами, столик и предмет приобретают разные ускорения: столик большее, предмет меньшее. В результате предмет, опережая столик, начнет скользить по его поверхности в направлении по ходу поезда. Если же сила трения, действующая на предмет, достаточна для того, чтобы сообщить предмету такое же точно ускорение, какое имеет столик, - никаких относительных перемещений происходить не будет: столик и предмет будут тормозиться или ускоряться как единое целое. Таким образом, инерционные эффекты объясняются не тем, что одни тела «сохраняют» свое движение (или покой) неизменным, а другие, напротив, изменяют, а тем, что изменение движения, изменение скорости всех взаимодействующих тел происходит неодинаково бы-стро: одни тела изменяют свое движение быстрее, другие медленнее. В результате мы наблюдаем относительные перемещения тел. И еще одно обстоятельство не следует забывать. Изменение скорости тела зависит не от одной только инерции (читай: массы) тела. Оно зависит также от величины силы и времени ее воздействия.
10 ДВИЖЕНИЕ ТЕЛА ПЕРЕМЕННОЙ МАССЫ 1. Особо следует сказать о динамике движения тела, масса которого изменяется за счет присоединения или отделения частиц. Например, масса падающей дождевой капли изменяется вследствие испарения молекул или, наоборот, их конденсации, масса ракеты или самолета изменяется за счет выбрасывания продуктов сгорания; в принципе, к телам с изменяющейся массой можно отнести автомобиль, тепловоз и т.д. 2. Движение тела переменной массы в общем случае может изменяться, во-первых, за счет воздействия внешних сил, во-вторых, за счет взаимодействия тела с отделяющимися (или присоединяющимися) частицами. У одних тел решающую роль в изменении скорости играют внешние силы (автомобиль, тепловоз, винтовой самолет), у других – силы, возникающие при взаимодействии с отделяющимися частицами (реактивный самолет, ракета). Закономерности движения тел переменной массы были подробно исследованы И.В.Мещерским и К.Э.Циолковским. Силы, возникающие при отделении (или присоединении) частиц, называются реактивными. Можно доказать в самом общем случае, что величина и направление реактивной силы, возникающей при отделении (или присоединении) частиц, зависит: 1) от быстроты изменения массы тела 2) от величины и направления скорости Как видно из этой формулы, реактивная сила, действующая на тело, совпадает по направлению с направлением присоединяются, и противоположна этой относительной скорости, если частицы отделяются. Поскольку на тело переменной массы всегда действует не только реактивная сила, но также и внешние силы (например, на ракету действует сила притяжения к Земле, Солнцу, сопротивление атмосферы и т.д.), ускорение такого тела будет определяться результирующей внешних и реактивных сил:
здесь
Учитывая (10.1), соотношение (10.2), можно переписать:
Последнее соотношение носит название уравнения Мещерского. Оно позволяет решать ряд важных прикладных задач механики.
11 ТРЕТИЙ ЗАКОН НЬЮТОНА
В этом и заключается суть третьего закона Ньютона: силы, с которыми взаимодействуют два тела, равны по величине и противоположны по направлению. 2. Одну из сил взаимодействия обычно называют силой «действия», другую – силой «противодействия». Не следует, однако, думать, что «действие» и «противодействие» чем-либо принципиально отличаются друг от друга. Обе силы совершенно равноправны и имеют одинаковую природу. Так, если «действующая» сила обусловлена упругой деформацией, то сила «противодействия» обусловлена также деформацией другого тела, с которым данное тело взаимодействует, если сила «действия» имеет гравитационное происхождение, то «противодействие» вызвано той же причиной и т.д. Любую из сил мы вправе назвать «действующей» и любую – «противодействующей». Изучая движение какого-либо тела, мы обычно указываем только те силы, которые действуют на это тело, и отвлекаемся от сил, приложенных к другим телам. Но эти силы существуют, и забывать о них, вообще говоря, не следует. Они позволяют лучше понять происхождение той или иной силы. Следует всегда помнить, что за каждой силой стоит реальное тело, с которым данное тело взаимодействует. Указывая силу, мы тем самым всегда указываем на два тела, которые взаимодействуют друг с другом. Так как силы действия и противодействия приложены к разным телам, то они не могут уравновесить друг друга. Если заменить силы в формуле (11.1) в соответствии со вторым законом Ньютона произведениями масс на ускорения, то третий закон Ньютона будет иметь вид:
т.е. ускорения, сообщаемые друг другу взаимодействующими телами, обратно пропорциональны их массам и направлены в противоположные стороны. Из третьего закона Ньютона непосредственно вытекает одно важное следствие: взаимодействие двух тел не может вызвать их перемещение в одном направлении. Чтобы оба взаимодействующих тела пришли в движение в одном направлении, необходимо, чтобы на одно из тел или на оба одновременно подействовало третье тело.
12 ХАРАКТЕРИСТИКА НЕКОТОРЫХ СИЛ, РАССМАТРИВАЕМЫХ В МЕХАНИКЕ Дадим краткую характеристику сил, рассматриваемых в механике. 1. Упругая сила – сила, возникающая при деформации тела, т.е. при изменении его формы или объема, обусловленном действием внешни х сил. Если после прекращения действия внешней силы, вызвавшей деформацию, тело полностью восстанавливает свою первоначальную форму и размеры, оно называется упругим. Упругими называются и деформации, возникающие в таком теле. Упругие тела обладают способностью оказывать сопротивление изменению их формы и объема. В таких телах возникают внутренние силы, препятствующие дальнейшему смещению частиц деформируемого тела, в результате чего внешние силы оказываются уравновешенными. Для упругих деформаций справедлив закон Гука: упругая сила, возникающая при деформации (например, при сжатии или растяжении), пропорциональна величине деформации:
Знак «минус» означает, что направление упругой силы всегда противоположно направлению смещения частиц тела (рис.11).
2. Сила всемирного тяготения обусловлена гравитационным взаимодействием материальных тел.
(материальные точки) или имеют сферическую форму и однородны, сила тяготения между ними численно равна
(закон всемирного тяготения Ньютона), где
|

 - распаде атомных ядер, не принято характеризовать при помощи понятия силы.
- распаде атомных ядер, не принято характеризовать при помощи понятия силы.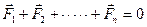
 . (8.1)
. (8.1) . Опыт покажет, что это отношение для данного тела является величиной постоянной. Обозначим эту величину буквой m:
. Опыт покажет, что это отношение для данного тела является величиной постоянной. Обозначим эту величину буквой m: (9.1)
(9.1) , (9.2)
, (9.2)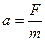 (9.3)
(9.3)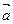 и
и  , получаем:
, получаем: 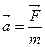 . (9.4)
. (9.4) (9.5)
(9.5)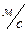 2). Единицей силы в системе СИ является ньютон (Н). Ньютон – это такая сила, под действием которой тело массой в 1 кг приобретает ускорение
2). Единицей силы в системе СИ является ньютон (Н). Ньютон – это такая сила, под действием которой тело массой в 1 кг приобретает ускорение  :
: .
. .
.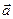 в формуле (9.4) нужно понимать результирующее ускорение, под
в формуле (9.4) нужно понимать результирующее ускорение, под  — геометрическую сумму всех действующих сил, а не какую-то «особую» силу ускорения:
— геометрическую сумму всех действующих сил, а не какую-то «особую» силу ускорения: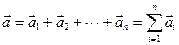
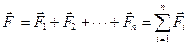
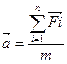 . (9.7)
. (9.7)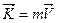 (9.8)
(9.8) . Под действием силы
. Под действием силы 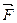 (она может быть переменной) за элементарный проме-жуток времени
(она может быть переменной) за элементарный проме-жуток времени 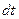 импульс тела изменился на
импульс тела изменился на  (в случае переменной силы промежуток времени
(в случае переменной силы промежуток времени  есть скорость изменения импульса.
есть скорость изменения импульса.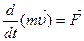 (9.9)
(9.9)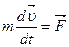 , но
, но  , следовательно,
, следовательно, 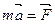 .
.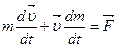 . (9.10)
. (9.10)
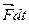 . (9.11)
. (9.11) и перепишем формулу (9.11):
и перепишем формулу (9.11): (9.12)
(9.12)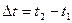 и одновременно подсчитаем импульс действующей силы за тот же промежуток. Для этого возьмем определенные интегралы от левой и правой частей соотношения (9.12):
и одновременно подсчитаем импульс действующей силы за тот же промежуток. Для этого возьмем определенные интегралы от левой и правой частей соотношения (9.12): . (9.13)
. (9.13)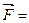 const, мы получим:
const, мы получим: 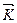 2 -
2 - 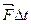 (9.14)
(9.14)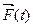 , то
, то 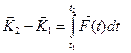 (9.15)
(9.15) (в случае присоединения частиц масса тела увеличивается, поэтому
(в случае присоединения частиц масса тела увеличивается, поэтому 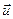 (относительно тела), с которой частицы покидают тело или присоединяются к нему:
(относительно тела), с которой частицы покидают тело или присоединяются к нему:  =
=  , (10.2)
, (10.2)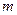 - масса тела в данный момент времени;
- масса тела в данный момент времени; 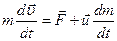 . (10.3)
. (10.3)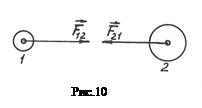 1. Опыт показывает, что воздействие одного тела на другое никогда не является односторонним. Если тело 1 действует на тело 2 с силой
1. Опыт показывает, что воздействие одного тела на другое никогда не является односторонним. Если тело 1 действует на тело 2 с силой  , то, в свою очередь, тело 2 действует на тело 1 с силой
, то, в свою очередь, тело 2 действует на тело 1 с силой  , причем силы взаимодействия равны по величине и противоположны по направлению (рис.10):
, причем силы взаимодействия равны по величине и противоположны по направлению (рис.10): = -
= -  . (11.1)
. (11.1)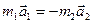 или
или 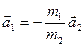 , (11.2)
, (11.2) , (12.1)
, (12.1)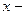 величина смещения (растяжения или сжатия);
величина смещения (растяжения или сжатия);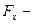 проекция упругой силы на направление смещения.
проекция упругой силы на направление смещения.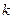 - так называемый коэффициент упругости – константа, характеризующая и вещество, и «геометрию» тела – его форму, размеры и т.д.
- так называемый коэффициент упругости – константа, характеризующая и вещество, и «геометрию» тела – его форму, размеры и т.д. - сила взаимного притяжения, действующая между любыми материальными телами или частицами,
- сила взаимного притяжения, действующая между любыми материальными телами или частицами,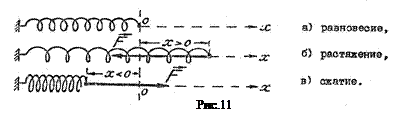 Если размеры тел малы по сравнению с расстоянием между ними
Если размеры тел малы по сравнению с расстоянием между ними , (12.2)
, (12.2)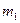 и
и 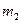 - массы тел;
- массы тел;  - рас
- рас


