Коэффициент напряженности работы. Анализ и оптимизация сетевого графика
После нахождения критического пути и резервов времени работ и оценки вероятности выполнения проекта в заданный срок должен быть проведен всесторонний анализ сетевого графика и приняты меры по его оптимизации. Этот весьма важный этап в разработке сетевых графиков раскрывает основную идею СПУ. Он заключается в приведении сетевого графика в соответствие с заданными сроками и возможностями организации, разрабатывающей проект. Вначале рассмотрим анализ и оптимизацию календарных сетей, в которых заданы только оценки продолжительности работ. Анализ сетевого графика начинается с анализа топологии сети, включающего контроль построения сетевого графика, установление целесообразности выбора работ, степени их расчленения. Затем проводятся классификация и группировка работ по величинам резервов. Следует отметить, что величина полного резерва времени далеко не всегда может достаточно точно характеризовать, насколько напряженным является выполнение той или иной работы некритического пути. Все зависит от того, на какую последовательность работ распространяется вычисленный резерв, какова продолжительность этой последовательности. Определить степень трудности выполнения в срок каждой группы работ некритического пути можно с помощью коэффициента напряженности работ. Коэффициентом напряженности К н работы (i, j) называется отношение продолжительности несовпадающих (заключенных между одними и теми же событиями) отрезков пути, одним из которых является путь максимальной продолжительности, проходящий через данную работу, а другим — критический путь:
где
Формулу (29) легко привести к виду
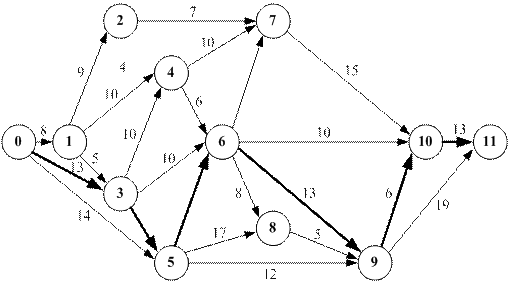
где Коэффициент напряженности Пример 4. Найти коэффициент напряженности работы (1, 4) для сетевого графика (рис. 6). Как было установлено ранее, длина критического пути t кр = 61 (сутки), а максимальный путь, проходящий через работу (1, 4) – путь L 4: 0→1→4→ 6→9→10→11 – имеет продолжительность t (L max) = t (L 4) = 49 (суток). Максимальный путь L 4 совпадает с критическим (см. рис. 6) на отрезке 6→9→10→11 продолжительностью . Или иначе: зная полный резерв времени R п(1,4) = 12 (см. табл. 3), по формуле (30) находим
Чем ближе к 1 коэффициент напряженности K н (i, j), тем сложнее выполнить данную работу в установленные сроки. Чем ближе K н (i, j) нулю, тем большим относительным резервом обладает максимальный путь, проходящий через данную работу. Работы могут обладать одинаковыми полными резервами, но степень напряженности сроков их выполнения, выражаемая коэффициентом K н (i, j), может быть различна. И наоборот, различным полным резервам могут соответствовать одинаковые коэффициенты напряженности. Так, полные резервы работ (3,6) и (6,7) для сетевого графика равны Rп(3,6) = Rп(6,7) = 10 (суток) – см. табл. 3, а их коэффициенты напряженности различны.
Обратим внимание на то, что больший полный резерв одной работы (по сравнению с другой) не обязательно свидетельствует о меньшей степени напряженности ее выполнения. Так, в рассматриваемой сети (см. рис. 14.6), хотя работа (2,7) обладает большим резервом времени по сравнению с работой (6,10) (Rп(2,7) = 23 > Rп(6,10) = 14), но имеет коэффициент напряженности Это объясняется разным удельным весом полных резервов работ в продолжительности отрезков максимальных путей, несовпадающих с критическим путем. Вычисленные коэффициенты напряженности позволяют дополнительно классифицировать работы по зонам. В зависимости от величины K н (i, j) выделяют три зоны: критическую (K н (i, j)>;0,8); подкритическую (0,6≤K н (i, j) ≤0,8); резервную (K н (i, j)<0,6). Оптимизация сетевого графика представляет процесс улучшения организации выполнения комплекса работ с учетом срока его выполнения. Оптимизация проводится с целью сокращения длины критического пути, выравнивания коэффициентов напряженности работ, рационального использования ресурсов. В первую очередь принимаются меры по сокращению продолжительности работ, находящихся на критическом пути. Это достигается: · Перераспределением всех видов ресурсов, как временных (использование резервов времени некритических путей), так и трудовых, материальных, энергетических (например, перевод части исполнителей, оборудования с некритических путей на работы критического пути); при этом перераспределение ресурсов должно идти, как правило, из зон, менее напряженных, в зоны, объединяющие наиболее напряженные работы; · сокращением трудоемкости критических работ за счет передачи части работ на другие пути, имеющие резервы времени; · параллельным выполнением работ критического пути; · пересмотром топологии сети, изменением состава работ и структуры сети. В процессе сокращения продолжительности работ критический путь может измениться, и в дальнейшем процесс оптимизации будет направлен на сокращение продолжительности работ нового критического пути и так будет продолжаться до получения удовлетворительного результата. В идеале длина любого из полных путей может стать равной длине критического пути или по крайней мере пути критической зоны. Тогда все работы будут вестись с равным напряжением, а срок завершения проекта существенно сократится. Весьма эффективным является использование метода статистического моделирования, основанного на многократных последовательных изменениях продолжительности работ (в заданных пределах) и "проигрывании" на компьютере различных вариантов сетевого графика с расчетами всех его временных параметров и коэффициентов напряженности работ. Процесс "проигрывания" продолжается до тех пор, пока не будет получен приемлемый вариант плана или пока не будет установлено, что все имеющиеся возможности улучшения плана исчерпаны и поставленные перед разработчиком проекта условия невыполнимы.
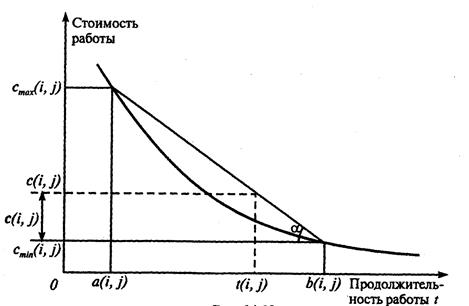
Оптимизация сетевого графика методом "время - стоимость"; Оптимизация сетевого графика в зависимости от полноты решаемых задач может быть условно разделена на частную и комплексную. Видами частной оптимизации сетевого графика являются: минимизация времени выполнения комплекса работ при заданной его стоимости; минимизация стоимости комплекса работ при заданном времени выполнения проекта. Комплексная оптимизация представляет собой нахождение оптимального соотношения величин стоимости и сроков выполнения проекта в зависимости от конкретных целей, ставящихся при его реализации. При использовании метода "время — стоимость" предполагают, что уменьшение продолжительности работы пропорционально возрастанию ее стоимости. Каждая работа (i, j) характеризуется продолжительностью t(i, j), которая может находиться в пределах a(i, j) ≤ t(i, j) ≤ b(i, j) (31)
где а (i, j) — минимально возможная (экстренная) продолжительность работы (i, j), которую только можно осуществить в условиях разработки; b(i,j) — нормальная продолжительность выполнения работы (i, j). При этом стоимость с(i, j) работы (i, j) заключена в границах с min (i, j) (при нормальной продолжительности работы) до c max (i, j) (при экстренной продолжительности работы). Используя аппроксимацию по прямой (см. рис. 12), можно легко найти изменение стоимости работы Δ с(i, j) при сокращении ее продолжительности на величину Δ с(i, j)= [ b(i, j)– t(i, j) ] h(i, j). (32) Величина h(i, j), равная тангенсу угла а наклона аппроксимирующей прямой (см. рис. 12), показывает затраты на ускорение работы (i,j) (по сравнению с нормальной продолжительностью) на единицу времени:
Рис. 12 – Зависимость стоимости работы от времени выполнения
Самый очевидный вариант частной оптимизации сетевого графика с учетом стоимости предполагает использование резервов времени работ. Продолжительность каждой работы, имеющей резерв времени, увеличивают до тех пор, пока не будет исчерпан этот резерв или пока не будет достигнуто верхнее значение продолжительности b(i,j). При этом стоимость выполнения проекта, равная до оптимизации
уменьшится на величину
Для проведения частной оптимизации сетевого графика кроме продолжительности работ t(i, j), необходимо знать их граничные значения а(i, j) и b(i, j), а также показатели затрат на ускорение работ h(i, j), вычисляемые по формуле (33). Продолжительность каждой работы t(i, j) целесообразно увеличить на величину такого резерва, чтобы не изменить ранние (ожидаемые) сроки наступления всех событий сети, т.е. на величину свободного резерва времени R c (i, j). Пример 5. Провести частную оптимизацию сетевого графика (рис. 6). Граничные значения продолжительностей работ a(i, j) и b(i, j), их стоимости с(i, j), коэффициенты затрат на ускорение работ h(i, j) приведены в табл. 4. Свободные резервы времени работ R c (i, j) были вычислены нами ранее (см.табл. 3). Их ненулевые значения даны в табл. 4. Там же представлены результаты частной оптимизации рассматриваемой сети.
Таблица 4
Примечания: 1. В таблице представлены параметры лишь тех работ, которые имеют свободный резерв времени. 2. Стоимости c(i,j) остальных работ: с (0,1)=50; с (0,3)=45; с (1,2)=82; c (3,4)=55; с (3,5)=72; с (5,6)=30; с (6,7)=26; с (6,9)=75; с (6,8)=42; с (9, 10)=35; с( 10,11)= 10 (усл.руб.). 3. Подчеркнуты те работы, свободные резервы времени которых полностью использованы на увеличение их продолжительности. Стоимость первоначального варианта сетевого графика или плана по. формуле (34) равна сумме стоимостей всех работ (включая работы, не имеющие резервов и не включенные в табл. 4): C=694+50+45+...+35+10=1216 (усл.руб.). Стоимость нового плана С – ΔС=1216 – 293=923 (усл.руб.), т.е. уменьшилась почти на 25%. Новый оптимизированный сетевой график представлен на рис. 13. Нетрудно убедиться в том, что появились новые критические пути длиной tкр=61 (сутки), например: 0→1→3→4→7→10→11; 0→3→5→8→9→11; 0→1→3→4→6→7→10→11; 0→3→5→6→8→9→11 и т.д.
Рис. 13 – Сетевой график после оптимизации
Можно показать, что в этом варианте сетевого графика из 64 полных путей 28 — критические. Если бы верхние границы продолжительностей работ дали возможность полностью использовать резерв времени всех работ, представленных в табл. 4, то в новом плане все полные пути были бы критические. Итак, в результате оптимизации сети мы пришли к плану, позволяющему выполнить комплекс работ в срок tкр=61 (сутки) при минимальной его стоимости С= 923 (усл.руб.).
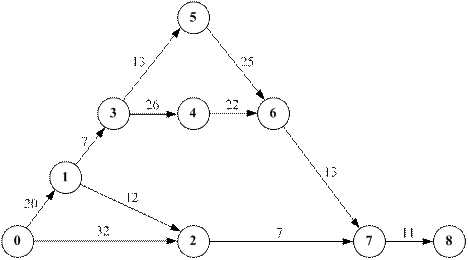
В реальных условиях выполнения проекта может потребоваться ускорение его выполнения, что, естественно, отразится на стоимости проекта: она увеличится. Поэтому необходимо определить оптимальное соотношение между стоимостью проекта С и продолжительностью его выполнения t = tкр, представленное, например, в виде функции С = С(t). Для оптимизации сетей и, в частности, для нахождения функции С(t) могут быть использованы эвристические методы, т.е. методы, учитывающие индивидуальные особенности сетевых графиков. Пример 6. Оптимизировать сетевой график, изображенный на рис. 14, в котором указаны максимально возможные продолжительности работ (в сутках). Необходимые для оптимизации исходные данные представлены в табл. 5. Таблица 5
Рис. 14 – Сетевой график к примеру 6
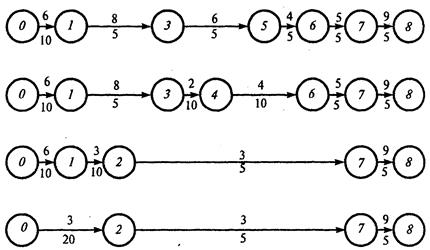
Исходный для оптимизации план (см.рис. 14) имеет максимальную продолжительность работ t(i, j)=b(i, j) и соответственно минимальную стоимость С=300 (усл.руб.). Найдем все полные пути сетевого графика. Их четыре: L1 0→1→3→5→6→7→8 продолжительностью t (L 1)=89 (суток); L2 0→1→3→4→6→7→8 продолжительностью tкр (L 2)=99 (суток); L3 0→1→2→7→8 продолжительностью t (L 3)=50 (суток); L4 0→2→7→8 продолжительностью t (L 4)=50 (суток). Для удобства дальнейших расчетов представим эти пути графически в виде цепочек работ (рис. 15), в которых цифры над стрелками показывают коэффициенты затрат на ускорение работ h(i, j), а под стрелками — максимально возможные величины уменьшения продолжительности работ Δ t(i, j) = b(i, j)–a(i, j).
Рис. 15 – Полные пути сетевого графика I шаг. Уменьшить продолжительность выполнения комплекса можно, как известно, только за счет сокращения продолжительности работ критического пути t кр= t(L 2 ). Из работ критического пути L 2наименьший коэффициент затрат на ускорение h(i, j) имеет работа (3,4): h min (i, j)= min{ h(0, 1); h(1, 3); h(3, 4); h(4, 6); h(6, 7); h(7,8) }=min{6; 8; 2; 4; 5; 9}=2, т.е. h min (i, j)=h(3, 4)=2. Продолжительность работы t (3,4) можно сокращать не более чем на 10 суток. При этом изменится длина только критического пути (с 99 до 89 суток) L2 — единственного из четырех путей, проходящего через работу (3,4). А стоимость проекта за счет ускорения работы (3,4) с учетом формул (14.34) и (14.35) возрастет до 300+2∙10=320 (усл.руб). Итак на I шаге: С = 300+2∙(99–t), где 89 ≤ t ≤ 99; Новые длины путей равны t(L 1 ) = t(L 2 )= 89; t(L 3 )= t(L 4 )= 50.
II шаг. Теперь мы имеем два критических пути L 1и L 2и сократить срок выполнения проекта можно за счет одновременного сокращения их продолжительности. Сократить одновременно t(L 1 ) и t(L 2 ) можно, уменьшив продолжительность работ, лежащих на этих путях (см. рис. 14.15): либо t(0, 1), либо t(6, 7), либо t(7, 8). Останавливаемся на t(6, 7), поскольку при этом обеспечивается минимум затрат на ускорение работы: h min(i, j)=min{ h (0, 1);h(1, 3); h(6, 7); h(7,8 }=min{6; 8; 5; 9}=5, т.е. h min(i, j)= h(6, 7)=5. Продолжительность работы t(6, 7), можно уменьшить не более чем на 5 суток. На эту величину уменьшатся длины критических путей t(L 1 ) и t(L 2 ), а следовательно, и срок выполнения проекта t=t(L 1 )=t(L 2 ). При этом стоимость проекта увеличится с 320 до 320+5∙5=345 (усл.руб.). Итак, на II шаге: С=320+5(89- t), где 84 ≤ t ≤89; t(L 1 )= t(L 2 )= 84, t(L 3 )= t(L 4 )= 50 Продолжая аналогичным образом сокращать продолжительность работ, получим
|

 (29)
(29) - продолжительность максимального пути, проходящего через работу (i, j);
- продолжительность максимального пути, проходящего через работу (i, j);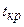 – продолжительность (длина) критического пути;
– продолжительность (длина) критического пути;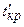 – продолжительность отрезка рассматриваемого пути, совпадающего с критическим путем.
– продолжительность отрезка рассматриваемого пути, совпадающего с критическим путем. (30)
(30) – полный резерв времени работы (i, j).
– полный резерв времени работы (i, j).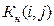 может изменяться в пределах от 0 (для работ, у которых отрезки максимального из путей, не совпадающие с критическим путем, состоят из фиктивных работ нулевой продолжительности) до 1 (для работ критического пути).
может изменяться в пределах от 0 (для работ, у которых отрезки максимального из путей, не совпадающие с критическим путем, состоят из фиктивных работ нулевой продолжительности) до 1 (для работ критического пути). .
.
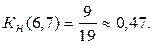
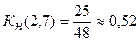 против
против 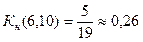 .
. (33)
(33)
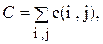 (34)
(34) (35)
(35)