III шаг

h _min(i, j)=min{ h (0, 1);h(1, 3); h(7,8 }=min{6; 8; 9}=6, т.е. h _min(i, j)= h (0, 1)= 6. сокращая продолжительность работы t(0, 1) до 10 суток, найдем

С=345+6∙(84– t), где 74 ≤ t ≤ 84;

t(L ₁ ) = t(L ₂ )= 74; t(L ₃ )= 40; t(L ₄ )= 50

 

IV шаг

h _min(i, j)=min{ h(1, 3); h(7,8 }=min{8; 9}=8, т.е. h _min(i, j)= h (1, 3)= 8. Сокращая продолжительность работы t(1, 3) до 5 суток, найдем

С=405+8∙(74– t), где 69 ≤ t ≤ 74;

t(L ₁ ) = t(L ₂ )= 69; t(L ₃ )= 40; t(L ₄ )= 50.

 

V шаг. Сокращая продолжительность работы t (7, 8) до 5 су­ток, найдем (учитывая, что h (7, 8)=9)

С=445+9∙(69– t), где 64 ≤ t ≤ 69;

t(L ₁ ) = t(L ₂ )= 64; t(L ₃ )= 35; t(L ₄ )= 45.

 

VI шаг. Теперь несокращенными остались продолжительности трех критических работ: t(3, 5) и t (5, 6) критического пути L ₁, каждую из которых можно сократить до 5 суток, и t(4, 6) кри­тического пути L ₂, которую можно сократить до 10 суток. Сокра­щение какой-либо одной из названных величин не приведет к сокращению продолжительности выполнения проекта, ибо при этом сократится лишь один из двух путей, а длина несокращенно­го пути, который станет единственным критическим путем, не изменится. Поэтому последовательно сокращая t (4, 6) и t (5, 6) до 5 суток (с учетом времени сокращения продолжительности работ), найдем (теперь коэффициент затрат на ускорение работ равен h(4, 6)+h(5, 6) = 4+4 = 8):

С=490+8∙(64– t), где 59 ≤ t ≤ 64;

t(L ₁ ) = t(L ₂ )= 59; t(L ₃ )= 35; t(L ₄ )= 45.

 

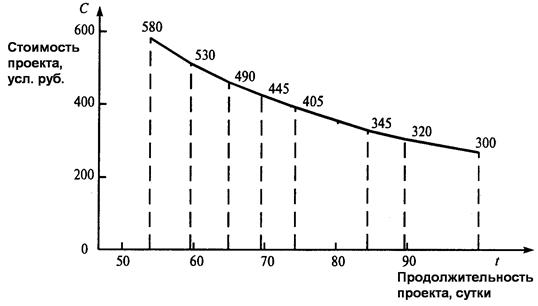
VII шаг. Продолжительность работы t(4, 6) можно сократить еще до 5 суток и на тот же срок можно сократить t(4, 6) (иначе срок выполнения проекта не изменится). Полагая, что h(4, 6) + h(3, 5)=4+6=10, найдем

С=530+10∙(59– t), где 54 ≤ t ≤ 59;

График оптимальной зависимости стоимости проекта С(t) от продолжительности его выполнения показан на рис. 16. С по­мощью этого графика можно, с одной стороны, оценить мини­мальную стоимость проекта при любом возможном сроке его вы­полнения, а с другой стороны — найти предельную продолжитель­ность выполнения проекта при заданной его стоимости. Например, при продолжительности проекта t =79 (суток) минимальная стои­мость выполнения рассматриваемого комплекса составит 375 (усл. руб.), а при стоимости выполнения комплекса, например, 540 (усл. руб.) предельная продолжительность проекта составит 55 (суток). С помощью функции С (t) можно оценить дополнительные затраты, связанные с сокращением сроков завершения комплекса.

Так, сокращение продолжительности проекта с 79 до 55 суток потребует дополнительных затрат 540—375=165 (усл. руб.).

 

Рис. 16 – Зависимость стоимости проекта от времени выполнения

 

Итак, мы рассмотрели один из возможных эвристических ал­горитмов оптимизации сетевого графика (см. рис. 14). Можно было использовать и другие алгоритмы. Например, взять в каче­стве первоначального план, имеющий не максимальные, а мини­мальные значения продолжительности работ t (i, j) = а (i, j) и со­ответственно максимальную стоимость проекта. А затем последо­вательно увеличивать продолжительность выполнения комплекса работ путем увеличения продолжительности работ, расположен­ных на некритических, а затем и на критическом (ских) пути в порядке убывания коэффициентов затрат h (i, j).

Следует заметить, что при линейной зависимости стоимости работ от их продолжительности задача построения оптимального сетевого графика может быть сформулирована как задача линей­ного программирования, в которой необходимо минимизировать стоимость выполнения проекта при двух группах ограничений. Первая группа ограничений показывает, что продолжительность каждой работы должна находиться в пределах, установленных неравенством (14.31). Вторая группа ограничений требует, чтобы продолжительность любого полного пути сетевого графика не превышала установленного директивного срока выполнения проекта. Однако решать такие задачи классическими методами ли­нейного программирования, как правило, неэффективно, в связи с чем используются специально разработанные методы.