Примеры
Задача 1. Сколько молекул кислорода находится в объеме 1 л при температуре 0° С и давление 133,3 Па? Решение Воспользуемся формулой, выражающей давление газа через концентрацию молекул
Откуда искомое число частиц
После подстановки значений, получим:
Задача 2. В баллоне объемом 10 л находится гелий под давлением p1=1 MПа и температуре T1=300 К. После того как из баллона было взято m=10 г гелия, температура в баллоне понизилась до T2=290 К. Определить давление p2 гелия, оставшегося в баллоне. Решение Выразим искомое давление из уравнения Менделеева-Клапейрона, применив его к конечному состоянию газа:
Массу гелия в баллоне в конечном состоянии m2 выразим через массу m1, соответствующую начальному состоянию, и массу m гелия, взятого из баллона
Массу m1 можно выразить из уравнения Менделеева-Клапейрона, применив его к начальному состоянию:
С учетом этого выражения масса m2
Окончательно для искомого уравнения имеем:
или
После подстановки значений, получим:
Задача 3. Определить давление и молекулярную массу смеси газов, состоящей из 10 г кислорода (О2) и 10 г азота (N2), которые занимают объем 20 л при температуре 150° С. Решение По закону Дальтона давление смеси газа
где парциальное давление pi каждого газа можно выразить из уравнения Менделеева-Клапейрона
Тогда давление смеси
После подстановки значений, получим:
Молярную массу смеси выразим через массу и количество вещества смеси газа
После подстановки значений, получим:
Задача 5. Давление газа равно 104 Па, а средняя квадратичная скорость равна 500 м/c. Найти плотность r этого газа. Решение Основное уравнение молекулярно-кинетической теории может быть представлено следующим образом:
Следовательно,
Задача 4. Какая часть молекул воздуха (M=29·10-3 кг/моль) при температуре 17°С обладает скоростями, отличающимися не более чем на 0,5 м/с от скорости u = uВ?
Решение Наиболее вероятная скорость
Относительная скорость и относительная величина интервала
Поскольку и согласно распределению Максвелла
Задача 6. Найти отношение числа молекул газа, скорости которых лежат в интервале от u до (u+ Решение Согласно распределению Максвелла, учитывая, что
где
Найдем отношение числа молекул газа:
Задача 7. На какой высоте h над уровнем моря плотность воздуха уменьшается в 2 раза? Температура воздуха 0° С. Считать, что температура воздуха Т, молярная масса M и ускорение силы тяжести g не зависят от h. Решение Исходя из определения плотности и с учетом уравнения Менделеева-Клапейрона имеем
Давление воздуха на высоте h в соответствиис барометрической формулой равно
Таким образом, плотность воздуха на высоте h дается выражением
После логарифмирования и преобразования данного выражения, получим окончательно
Задача 8. Определить массу m газа, заключенного в вертикальном цилиндрическом сосуде. Площадь основания сосуда S, высота h. Давление газа на уровне нижнего основания цилиндра p0, температура газа Т, молярная масса газа M. Считать, что Т и g не зависит от h. Решение Поскольку давление, а, следовательно, и плотность газа, заключенного в вертикальном сосуде, зависит от высоты, то массу газа необходимо находить путем интегрирования выражения
С учетом того, что плотность газа уменьшается с высотой согласно закону
Приведем данный интеграл к табличному виду, используя метод замены переменной:
Откуда
|

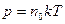 =
= 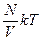 .
.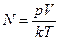 .
.
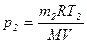 .
.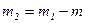 .
. .
. .
.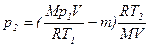 ,
, .
.
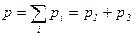 ,
, .
.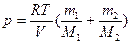 .
.

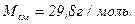
 .
. кг/м3.
кг/м3. .
.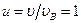 ;
; 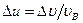 = 1,2×10-3.
= 1,2×10-3. можно считать, что
можно считать, что 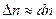 ,
, 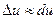
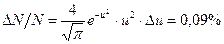 .
. ) при температуре Т1 к числу молекул, скорости которых лежат в том же интервале при температуре Т2 = 2Т1. Считать, что
) при температуре Т1 к числу молекул, скорости которых лежат в том же интервале при температуре Т2 = 2Т1. Считать, что 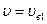 ,
, 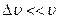 .
.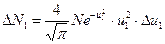 ,
,  ,
,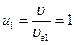 ,
, 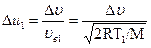 ;
;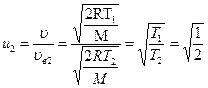 ,
, 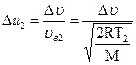 .
.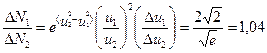 .
.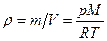 .
.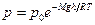 .
.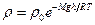 .
. =5,4 км.
=5,4 км.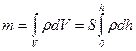 .
.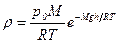 , получим
, получим .
.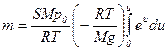 , где
, где  .
.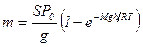 .
.


