Классическая электронная теория дисперсии
В диэлектриках скорость световых ЭМВ зависит от частоты. Это явление называется дисперсией. Дисперсия проявляется лишь в распространении немонохроматических волн, т.к. ее монохроматические составляющие с различными частотами распространяются с различными скоростями. Дисперсия является следствием зависимости поляризованности атомов от частоты. Для нахождения явного вида e(w), входящей в материальные уравнения, воспользуемся микроскопической классической теорией взаимодействия электромагнитного поля волны с веществом. Микроскопическая теория исходит из некоторой идеализированной модели строения вещества. Наибольшей простотой отличается модель газообразной среды, т.к. для нее в первом приближении можно не учитывать взаимодействие атомов или молекул и считать, что действующее на отдельный атом поле совпадает со средним полем ЭМВ. В таких условиях для получения макроскопического материального уравнения достаточно рассмотреть действие поля ЭМВ на изолированный атом. Вообще говоря, применять классическую теорию к таким процессам нужно крайне осторожно. Но в данном случае квантовая теория дисперсии приводит к таким же результатам, что и классическая. В классической теории дисперсии электрон, с которым взаимодействует электромагнитное поле (внешний, или оптический электрон), в атоме рассматривается как затухающий дипольный осциллятор, характеризуемый определенной собственной частотой wо и постоянной затухания g, так что уравнение его движения в поле E (t) = E oe– i wt световой волны имеет вид:
где r – смещение электрона из положения равновесия, e и m – заряд и масса электрона. Будем искать решение этого уравнения в виде:
В результате получим:
Дипольный момент атома p (t), индуцированный полем E (t):
Если N – концентрация электронов с собственной частотой колебаний w0, то поляризованность P среды определяется следующим образом:
С другой стороны поляризованность среды (поляризация среды) равна
где c – линейная диэлектрическая восприимчивость среды, которая вообще говоря, зависит от частоты w. Учтем также, что векторы D, E и P связаны соотношением:
Тогда из (3.10) и (3.11) следует, что для относительной проницаемости:
а из (3.8), (3.9), (3.10) имеем:
или
Т.к.
Тогда с учетом (3.14) имеем уравнения:
Для прозрачных или частично прозрачных в оптическом диапазоне диэлектриков g очень мало. Тогда
Из этого приближения получаем:
Если в среде дисперсию определяют различные ансамбли электронов с собственными частотами w0 i и концентрацией Ni, то формулу (3.18) можно обобщить:
В этой формуле не учтены колебания ионов. Т.к. их масса много больше массы электронов, то собственные частоты ионов лежат в дальней инфракрасной области. Нормальная дисперсия. Вдали от собственных резонансов величина
Тогда
Графическая зависимость
Рис. 3.1
Если действительная часть показателя преломления увеличивается с ростом частоты, то дисперсия называется нормальной. Нормальная дисперсия наблюдается во всей области прозрачности диэлектриков. Для малых частот (w << w0 i) формула (3.21) дает статическое значение показателя преломления:
Это значение может существенно отличаться от значения показателя преломления для оптических частот. Например, для воды в области оптических частот n = 1,33, а статическое значение Для больших частот (w >> w0 i)
Таким образом, для коротковолнового излучения диэлектрик является оптически менее плотной средой, чем вакуум. Например, для рентгеновского излучения может наблюдаться полное отражение. Кроме того, при очень больших частотах характер связи электронов роли не играет, а показатель преломления n зависит лишь от общей концентрации всех электронов.
Аномальная дисперсия. Пренебрежение затуханием (g = 0) привело к тому, что
Дисперсионные кривые (3.24) представлены на рис.3.2.
Вблизи резонансной частоты w0 показатель преломления Мнимая часть показателя преломления в общем случае определяет величину поглощения. Поэтому область аномальной дисперсии соответствует области поглощения световых волн данным веществом. Именно это и используется для целей спектроскопии веществ.
|

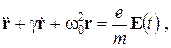 (3.5)
(3.5)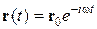 . (3.6)
. (3.6)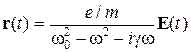 . (3.7)
. (3.7)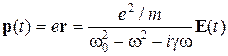 . (3.8)
. (3.8) . (3.9)
. (3.9)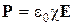 , (3.10)
, (3.10)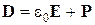 . (3.11)
. (3.11)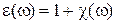 , (3.12)
, (3.12) (3.13)
(3.13) . (3.14)
. (3.14)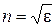 , то это значит, что показатель преломления, а следовательно, и скорость ЭМВ зависят от частоты. Видно также, что n – комплексная величина:
, то это значит, что показатель преломления, а следовательно, и скорость ЭМВ зависят от частоты. Видно также, что n – комплексная величина: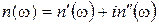 . (3.15)
. (3.15)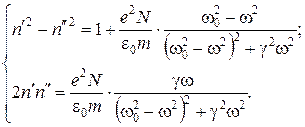 (3.16)
(3.16)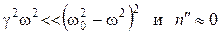 . (3.17)
. (3.17)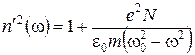 . (3.18)
. (3.18)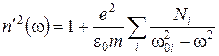 . (3.19)
. (3.19)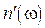 близка к 1 (для прозрачных диэлектриков, разреженных газов):
близка к 1 (для прозрачных диэлектриков, разреженных газов):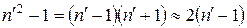 . (3.20)
. (3.20) . (3.21)
. (3.21)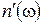 (дисперсионная кривая) имеет вид рис.3.1.
(дисперсионная кривая) имеет вид рис.3.1.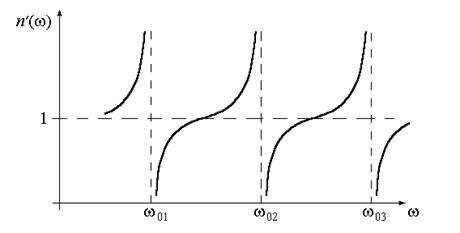
 . (3.22)
. (3.22)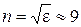 .
.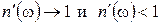 , при этом
, при этом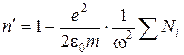 . (3.23)
. (3.23) при w = w0 i. Но вблизи собственных частот нельзя пренебречь g. Тогда
при w = w0 i. Но вблизи собственных частот нельзя пренебречь g. Тогда 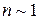 ):
):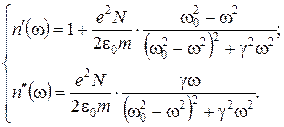 (3.24)
(3.24)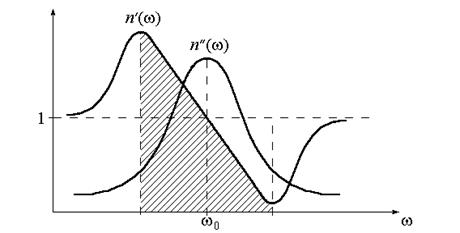 Рис. 3.2
Рис. 3.2



