Отражение и преломление света на границе двух диэлектриков.
Граничные условия для векторов поля световой волны на границе между двумя диэлектриками при отсутствии свободных зарядов и токов проводимости имеют вид:
где t, n – индексы тангенциальной (касательной к границе раздела) и нормальной компоненты вектора соответственно.
Пусть на плоскую границу двух диэлектриков с абсолютными (не относительными!) проницаемостями (e1; m1) и (e2; m2) (магнитную проницаемость пока оставим в общем виде) падает под некоторым углом плоская световая волна (рис.3.3). Тогда для напряженностей электрического поля в падающей, отраженной и преломленной волнах соответственно имеем:
где Законы отражения и преломления света на границе полностью определяются граничными условиями (3.25) и (3.26). Для электрического поля с учетом (3.27) граничные условия принимают вид:
Отметим, что начало отсчета вектора r (точка 0’) совершенно произвольно. Если 0’ лежит не на поверхности раздела, то
При этом в (3.28): Равенство (3.28) будет соблюдаться для произвольных значений r и t только при
Отсюда следует, что частота ЭМВ при отражении и преломлении не меняется:
Выберем точку 0’ так, чтобы вектор Плоскость, в которой лежат волновой вектор k 0 и нормаль к поверхности раздела n в точке падения луча, называется плоскостью падения. Из рис.3.3 видно, что
Тогда с учетом (3.31) получаем:
или из (3.27) и (3.32):
Вспомним, что
1)
2) (Закон преломления или з акон Снеллиуса) (Snellius Willebord 1591–1626) Введем обозначение
Тогда закон Снеллиуса примет вид:
При
Вообще говоря, вектор E 0 в падающей волне может иметь произвольный азимут a (угол между E и плоскостью падения. Разложим векторы электромагнитного поля на две составляющие: перпендикулярные плоскости падения (будем обозначать их индексом s (или ^) и параллельные плоскости падения (будем обозначать их индексом p (или ||)) (рис.3.6):
Видно, что векторы Отражение и преломление s- поляризованной ЭМВ. (Рис.3.7)
Введем единичные векторы в направлении волновых векторов:
Как направлены векторы E 1 и E 2 заранее не известно. Направим условно их так, как показано на рис.3.7. Если знак получится отрицательный, значит векторы направлены в противоположную сторону. Граничные условия для s –поляризации (индексы s опустим):
Обозначим
Из рис.3.7 можно найти связь
Для дальнейшего использования в (3.43) получим из (3.44) и (3.45) скалярное произведение для любой из рассматриваемых волн:
С учетом известной из векторного анализа формулы
получаем:
Тогда из (3.43) имеем:
Соотношения (3.49) и (3.42) совместно можно записать в виде:
Обозначим:
Учтем, что
При
(Обобщенные формулы Френеля для s – поляризации)
Для диэлектриков в оптическом диапазоне обычно
Графики зависимостей
При отражении света от диэлектрика с При отражении света от диэлектрика с Отражение и преломление p– поляризованной ЭМВ. (Рис.3.9)
Рассмотрение в данном случае проводится аналогично случаю s -поляризации. Для этого учтем, что
Отсюда
Граничные условия для p –поляризации принимают вид:
Подставляя (3.60) в (3.61), получаем:
Для действительных углов преломления получаем обобщенные формулы Френеля для p–поляризации:
или для диэлектриков с m1 = m2:
Графики зависимостей
Явление Брюстера. Из формулы (3.67) и из графика рис.3.10 видно, что для p –поляризованной волны при некотором угле падения
Заметим, что явлениие Брюстера наблюдается тогда, когда направления преломленной и отраженной волны ортогональны. С физической точки зрения это можно объяснить следующим образом. Если связывать наличие отраженной волны с вынужденными колебаниями электронов во второй среде, то в направлении, перпендикулярном преломленной волне, не должна распространяться энергия, т.к. образующийся при этом диполь не излучает в направлении собственных колебаний. При переходе через угол Брюстера фаза колебаний отраженной волны скачком меняется на p. При
При нормальном падении света (
Энергетические соотношения при преломлении и отражении. Энергетическим коэффициентом отражения
Энергетический коэффициент пропускания
Т.к.
то для Â имеем:
или с учетом (3.54), (3.55), (3.65), (3.66):
При q0 = 0 для m1 = m2
Прямой проверкой можно показать, что
Это выражает закон сохранения энергии при отражении и преломлении света на границе раздела двух сред. Графики для
Явление полного внутреннего отражения. При падении света на границу двух диэлектриков, для которых Тогда
При
Когда угол падения
Но формулы Френеля останутся справедливыми и в этом случае, если закон преломления рассматривать просто как определение входящих в них величин sinq2 и cosq2 в соответствии с (3.86). Справедливость понимаемых таким образом формул Френеля следует из того, что они обеспечивают выполнение граничных условий и в этом случае. Рассмотрим сначала световую волну во второй среде (преломленную) в общем случае:
В такой записи сомножитель I означает комплексную амплитуду волны II, распространяющейся вдоль оси X со скоростью
Знак (+) в первой экспоненте соответствует безграничному возрастанию поля в среде, что лишено физического смысла. Поэтому остается (–), что соответствует быстро убывающей с ростом z амплитуде волны, распространяющейся во второй среде вдоль X. Практически эта неоднородная волна существует лишь в поверхностном слое второй среды толщиной порядка длины волны. Причем фазовая скорость этой неоднородной (и соответственно не плоской) зависит как от свойств среды, так и от угла падения. Формулы Френеля для отраженной волны ((3.56) и (3.67) с учетом (3.86)) имеют вид:
Видно, что энергетические коэффициенты
движутся вдоль поверхности раздела и затем возвращаются в первую среду. Места входа энергии во вторую среду и ее возвращения в первую смещены друг относительно друга. Амплитуды p– и s– компонент отраженной волны не изменяются по абсолютному значению, но испытывают различные фазовые сдвиги. Если представить, что
то
Обозначим Тогда
Примеры: 1. Призма–крыша. 2. Световоды. 3. Миражи. 4. Ромб (параллелепипед) Френеля (
|

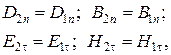 (3.25) – (3.26)
(3.25) – (3.26) Рис. 3.3
Рис. 3.3
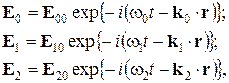 (3.27)
(3.27) ‑ волновые числа,
‑ волновые числа,  – скорости света в 1-й и 2-й средах.
– скорости света в 1-й и 2-й средах.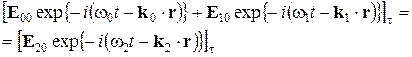 (3.28)
(3.28)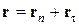 . (3.29)
. (3.29)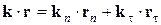 . Но для любой точки поверхности
. Но для любой точки поверхности 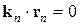 , поэтому удобно точку 0’ поместить на границе раздела.
, поэтому удобно точку 0’ поместить на границе раздела. (3.30)
(3.30)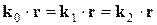 . (3.31)
. (3.31)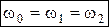 . (3.32)
. (3.32)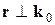 (т.е. направим перпендикулярно плоскости XZ рис.3.3). Тогда
(т.е. направим перпендикулярно плоскости XZ рис.3.3). Тогда 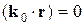 , а из (3.31) следует, что и
, а из (3.31) следует, что и  . Отсюда следует, что волновые векторы падающей, отраженной и преломленной волн лежат в одной плоскости.
. Отсюда следует, что волновые векторы падающей, отраженной и преломленной волн лежат в одной плоскости. (3.33)
(3.33)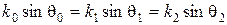 (3.34)
(3.34) . (3.35)
. (3.35)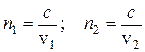 – показатели преломления. Из (3.35) можно сделать следующие выводы:
– показатели преломления. Из (3.35) можно сделать следующие выводы: . (3.36)
. (3.36)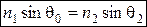 . (3.37)
. (3.37)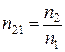 – относительный показатель преломления. (3.38)
– относительный показатель преломления. (3.38) . (3.39)
. (3.39) (падение из менее оптически плотной в более оптически плотную среду)
(падение из менее оптически плотной в более оптически плотную среду) 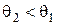 (рис.3.4). При
(рис.3.4). При 
 (рис.3.5).
(рис.3.5). Рис. 3.4
Рис. 3.4
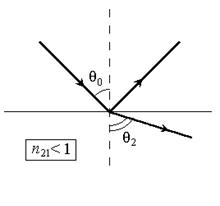 Рис. 3.5
Рис. 3.5
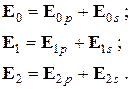 (3.40)
(3.40)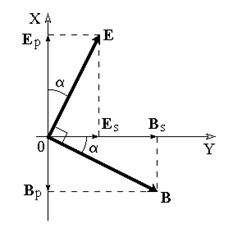 Рис. 3.6
Рис. 3.6
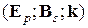 и
и  составляют правовинтовые тройки векторов и образуют сами плоские ЭМВ. Кроме этого видно, что
составляют правовинтовые тройки векторов и образуют сами плоские ЭМВ. Кроме этого видно, что  , т.е. плотность потока энергии исходной волны равна сумме плотностей потока энергии волн, на которые она разлагается. Т.о., плоскую волну с произвольным азимутом можно разложить на сумму волн, у одной из которых E p (p – поляризация) лежит в плоскости падения, а у другой E s (s – поляризация) – перпендикулярна ей. Изучив поведение этих волн на границе с учетом принципа суперпозиции и аддитивности (в данном случае) плотностей потока энергии, получим поведение ЭМВ с произвольным азимутом.
, т.е. плотность потока энергии исходной волны равна сумме плотностей потока энергии волн, на которые она разлагается. Т.о., плоскую волну с произвольным азимутом можно разложить на сумму волн, у одной из которых E p (p – поляризация) лежит в плоскости падения, а у другой E s (s – поляризация) – перпендикулярна ей. Изучив поведение этих волн на границе с учетом принципа суперпозиции и аддитивности (в данном случае) плотностей потока энергии, получим поведение ЭМВ с произвольным азимутом.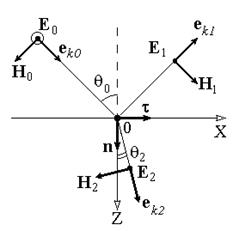 Рис. 3.7
Рис. 3.7
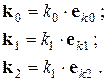 (3.41)
(3.41)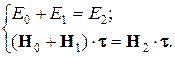 (3.42) – (3.43)
(3.42) – (3.43) – волновое сопротивление (импеданс)среды. (Для вакуума
– волновое сопротивление (импеданс)среды. (Для вакуума 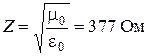 .) В оптике, в отличие от электричества, понятие волнового сопротивления среды практически не используется. Но для удобства записи мы им временно воспользуемся. Тогда
.) В оптике, в отличие от электричества, понятие волнового сопротивления среды практически не используется. Но для удобства записи мы им временно воспользуемся. Тогда . (3.44)
. (3.44) :
: . (3.45)
. (3.45) . (3.46)
. (3.46) (3.47)
(3.47) . (3.48)
. (3.48)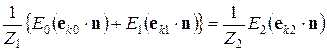 . (3.49)
. (3.49) (3.50)
(3.50) – амплитудный коэффициент отражения; (3.51)
– амплитудный коэффициент отражения; (3.51) – амплитудный коэффициент пропускания. (3.52)
– амплитудный коэффициент пропускания. (3.52) (3.53)
(3.53) система (3.50) имеет действительное решение для всех углов q0. Если
система (3.50) имеет действительное решение для всех углов q0. Если  она имеет действительное решение лишь для углов
она имеет действительное решение лишь для углов  (подробнее этот случай рассмотрим позднее). Тогда имеем:
(подробнее этот случай рассмотрим позднее). Тогда имеем: (3.54) – (3.55)
(3.54) – (3.55) . Тогда из (3.54) и (3.55) получим общепринятые формулы Френеля для диэлектриков для s – поляризации:
. Тогда из (3.54) и (3.55) получим общепринятые формулы Френеля для диэлектриков для s – поляризации: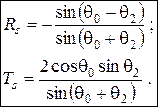 (3.56) – (3.57)
(3.56) – (3.57)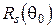 и
и  для
для 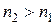 приведены на рис.3.8.
приведены на рис.3.8.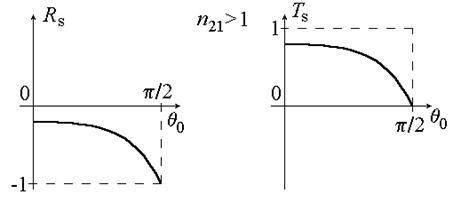 Рис. 3.8
Рис. 3.8
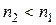 скачка фазы на p не происходит ни для отраженной, ни для преломленной волны (для углов
скачка фазы на p не происходит ни для отраженной, ни для преломленной волны (для углов  , т.е. для случая полного внутреннего отражения фаза ведет себя сложнее, это рассмотрение – ниже).
, т.е. для случая полного внутреннего отражения фаза ведет себя сложнее, это рассмотрение – ниже). Рис. 3.9
Рис. 3.9
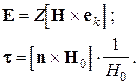 (3.58) – (3.59)
(3.58) – (3.59) . (3.60)
. (3.60)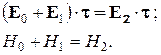 (3.61) – (3.62)
(3.61) – (3.62) ; (3.63)
; (3.63) . (3.64)
. (3.64)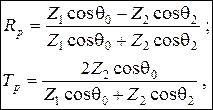 (3.65) – (3.66)
(3.65) – (3.66)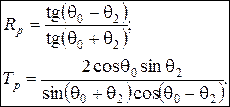 (3.67) – (3.68)
(3.67) – (3.68) и
и  для
для  Рис. 3.10
Рис. 3.10
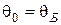 , называемом углом Брюстера, отраженная волна отсутствует, т.е.
, называемом углом Брюстера, отраженная волна отсутствует, т.е.  . Это называется явлением Брюстера (Brewster David, 1781 – 1868) (1815 г.). Для угла Брюстера справедливы следующие соотношения:
. Это называется явлением Брюстера (Brewster David, 1781 – 1868) (1815 г.). Для угла Брюстера справедливы следующие соотношения: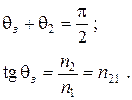 (3.69)
(3.69) Пример. Стопа Столетова (рис.3.11). При падении неполяризованного света на стопу Столетова, состоящую из N плоскопараллельных стеклянных пластин с воздушным зазором между ними,
Пример. Стопа Столетова (рис.3.11). При падении неполяризованного света на стопу Столетова, состоящую из N плоскопараллельных стеклянных пластин с воздушным зазором между ними,  s -компонента волны на каждой поверхности частично отражается, а p -компонента всё время проходит полностью. На выходе – практически линейно-поляризованный свет.
s -компонента волны на каждой поверхности частично отражается, а p -компонента всё время проходит полностью. На выходе – практически линейно-поляризованный свет. ) понятия s– и p – поляризаций теряют смысл и формулы (3.54), (3.55), (3.65) и (3.66) дают один и тот же результат (для диэлектрика
) понятия s– и p – поляризаций теряют смысл и формулы (3.54), (3.55), (3.65) и (3.66) дают один и тот же результат (для диэлектрика  ):
): (3.70) – (3.71)
(3.70) – (3.71) называется абсолютное значение отношения нормальных компонент векторов Пойнтинга в отраженной и падающих волнах:
называется абсолютное значение отношения нормальных компонент векторов Пойнтинга в отраженной и падающих волнах: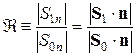 . (3.72)
. (3.72)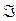 вводится аналогичным образом для преломленной волны:
вводится аналогичным образом для преломленной волны: . (3.73)
. (3.73) , (3.74)
, (3.74) (3.75)
(3.75)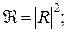 (3.76)
(3.76) (3.77)
(3.77)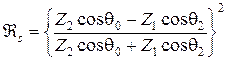 ; (3.78)
; (3.78)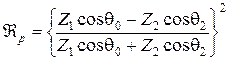 ; (3.79)
; (3.79)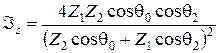 ; (3.80)
; (3.80) . (3.81)
. (3.81)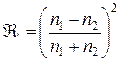 ; (3.82)
; (3.82) . (3.83)
. (3.83)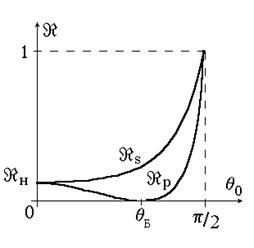 Рис. 3.12
Рис. 3.12
 . (3.84)
. (3.84)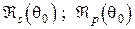 изображены на рис.3.12.
изображены на рис.3.12. Рис. 3.13
Рис. 3.13
 (рис.3.13), из закона Снеллиуса следует, что существует предельный (или критический) угол qп падения, при котором угол преломления
(рис.3.13), из закона Снеллиуса следует, что существует предельный (или критический) угол qп падения, при котором угол преломления 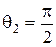 .
.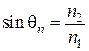 . (3.85)
. (3.85)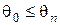 угол преломления q2 имеет обычную геометрическую интерпретацию, и коэффициенты R и T являются вещественными.
угол преломления q2 имеет обычную геометрическую интерпретацию, и коэффициенты R и T являются вещественными. , не существует вещественного угла преломления q2, т.к. закон Снеллиуса дает для sinq2 значение больше единицы, а для cosq2 – чисто мнимое значение:
, не существует вещественного угла преломления q2, т.к. закон Снеллиуса дает для sinq2 значение больше единицы, а для cosq2 – чисто мнимое значение: (3.86)
(3.86)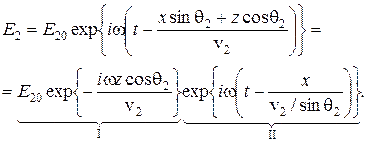 (3.87)
(3.87)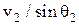 . Подставим (3.86) в (3.87):
. Подставим (3.86) в (3.87): . (3.88)
. (3.88)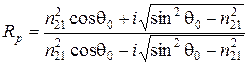 ; (3.89)
; (3.89) . (3.90)
. (3.90) Рис. 3.14
Рис. 3.14
 при углах падения больше критического (рис.3.14). Поэтому это явление называется полным внутренним отражением(ПВО). При этом волна и соответствующая доля энергии проникают через границу раздела во вторую среду на некоторую глубину d (глубину проникновения) (амплитуда поля на глубине d падает в е раз):
при углах падения больше критического (рис.3.14). Поэтому это явление называется полным внутренним отражением(ПВО). При этом волна и соответствующая доля энергии проникают через границу раздела во вторую среду на некоторую глубину d (глубину проникновения) (амплитуда поля на глубине d падает в е раз):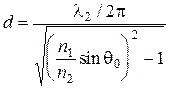 , (3.91)
, (3.91) , (3.92)
, (3.92) (3.93)
(3.93)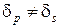 .
.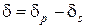 . (3.94)
. (3.94)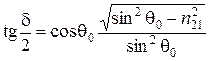 . (3.95)
. (3.95) ).
).


