Выпуклость, вогнутость, точки перегиба графика функции. Исследование функции на перегиб.
Практическая работа № 19 Нахождение точек перегиба, интервалов выпуклости и вогнутости Цель работы:проверить умения и знания по нахождению интервалов выпуклости и вогнутости, точек перегиба. Теоретический материал. Выпуклость, вогнутость, точки перегиба графика функции. Исследование функции на перегиб.
Кривая называется выпуклой в точке Кривая называется вогнутой в точке Точка, в которой меняется направление выпуклости и вогнутости, называется точкой перегиба. Промежутки, в которых график функции выпуклый или вогнутый, называются промежутками выпуклости. Выпуклость характеризуется знаком второй производной: Теорема: Если вторая производная функции Алгоритм нахождения интервалов выпуклости:
Если в некотором промежутке вторая производная положительна, то функция на нем вогнута, если – отрицательна, то выпукла Пример 1: Найти промежутки выпуклости кривой Решение:
Пример 2. Найти точки перегиба кривой Решение:
Пример. Исследовать функцию
1. D(y)= 2.E(y)= 3. 4. 5. Найдем наклонные асимптоты.
6.
Критические точки:
Находим промежутки возрастания и убывания функции. Для этого определяем знаки производной функции на промежутках.
-¥ < x < - - -1 < x < 0, y¢ < 0, функция убывает 0 < x < 1, y¢ < 0, функция убывает 1 < x <
7.
Определим выпуклость и вогнутость кривой на промежутках.
-¥ < x < - - -1 < x < 0, y¢¢ > 0, кривая вогнутая 0 < x < 1, y¢¢ < 0, кривая выпуклая 1 < x <
Видно, что точка х = -
|

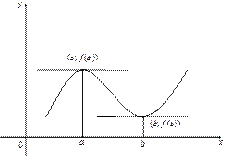
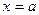 , если в некоторой окрестности этой точки она расположена под своей касательной в точке
, если в некоторой окрестности этой точки она расположена под своей касательной в точке 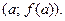
 , если в некоторой окрестности этой точки она расположена над своей касательной в точке
, если в некоторой окрестности этой точки она расположена над своей касательной в точке 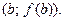
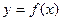 в данном промежутке положительна, то кривая вогнута в этом промежутке, а если отрицательна – выпукла в этом промежутке.
в данном промежутке положительна, то кривая вогнута в этом промежутке, а если отрицательна – выпукла в этом промежутке.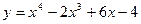
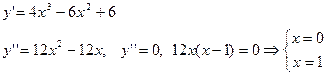
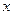
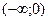
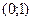
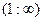
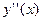
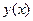
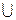
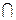
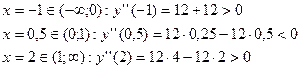

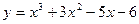
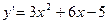
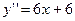
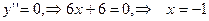
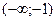
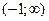
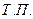
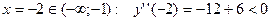
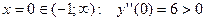
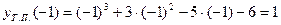 . Точка перегиба
. Точка перегиба 
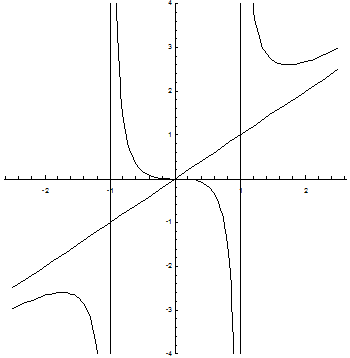
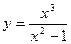 и построить ее график.
и построить ее график.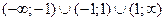
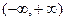
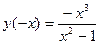 - функция нечетная, график симметричен относительно начала координат, непериодичная
- функция нечетная, график симметричен относительно начала координат, непериодичная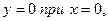
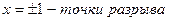
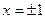 - вертикальные асимптоты
- вертикальные асимптоты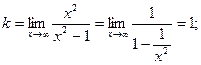
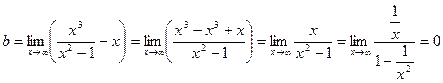
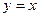 - уравнение наклонной асимптоты.
- уравнение наклонной асимптоты.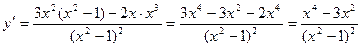
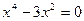
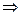
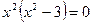

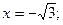
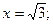
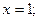
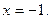
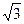 , y¢ > 0, функция возрастает
, y¢ > 0, функция возрастает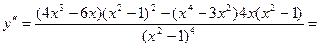
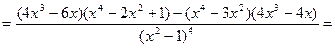

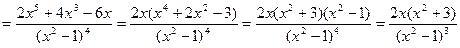 .
.