Задание к работе
Исходные данные смоделированы на основе линейной эконометрической модели:
где случайные величины Исходные данные представляют собой двумерную выборку
По выборке необходимо построить парную линейную регрессию и проверить ее статистическую значимость.
1. Для заданных исходных данных постройте поле корреляции — диаграмму зависимости показателя При построении выберите тип диаграммы «Точечная» (без отрезков, соединяющих точки). 2*. Вычислите выборочные характеристики: — выборочные средние — выборочные дисперсии — выборочное среднее квадратические отклонения — выборочный коэффициент корреляции 3. Вычислите коэффициенты выборочной линейной регрессии. Для вычисления коэффициентов регрессии воспользуйтесь встроенной функцией ЛИНЕЙН (функция находится в категории «Статистические»), обратите внимание, что эта функция является функцией массива, поэтому ее использование подразумевает выполнение следующих шагов: 1) В свободном месте рабочего листа выделите область ячеек размером 5 строк и 2 столбца для вывода результатов; 2) В Мастере функций (категория «Статистические») выберите функцию ЛИНЕЙН. 3) Заполните поля аргументов функции: Известные_значения_y — адреса ячеек, содержащих значения признака Известные_значения_x — адреса ячеек, содержащих значения фактора Константа — значение (логическое), указывающее на наличие свободного члена в уравнении регрессии: укажите в поле Константа значение 1, тогда свободный член рассчитывается обычным образом (если значение поля Константа равно 0, то свободный член полагается равным 0); Статистика — значение (логическое), которое указывает на то, следует ли выводить дополнительную информацию по регрессионному анализу или нет: укажите в поле Статистика значение равное 1, тогда будет выводиться дополнительная регрессионная информация (если Статистика=0, то выводятся только оценки коэфициентов уравнения регрессии); 4) После того, как будут заполнены все аргументы функции, нажмите комбинацию клавиш <CTRL>+<SHIFT>+<ENTER>. Результаты расчета параметров регрессионной модели будут выведены в виде следующей таблицы:
4*. Проверьте полученные значения коэффициентов 5. Запишите найденной уравнение эмпирической регрессии. Дайте интерпретацию коэффициенту 6. Постройте на корреляционном поле прямую выборочной линейной регрессии по точкам 7. Вычислите остатки 8. Постройте график остатков (тип диаграммы — «Точечная»). 9. Найдите величину средней ошибки аппроксимации 10*. Вычислите коэффициент детерминации 11*. Рассчитайте значение 12. Вычислите значения Вероятность — уровень значимости Степени_свободы — число степеней свободы, для парной линейной регрессии равно 13. Проверьте значимость в целом полученного уравнения регрессии по критерию Фишера. Значение Вероятность — уровень значимости Степени_свободы1 — число степеней свободы числителя, для парной регрессии равно 1 (т.к. один фактор); Степени_свободы2 — число степеней свободы знаменателя, для парной регрессии равно 14. Вычислите доверительные интервалы параметров линейной регрессии. Дайте им интерпретацию. 15. Постройте прогноз 16. Вычислите стандартные ошибки прогноза функции регрессии (среднего значения) и индивидуального значения, постройте доверительные интервалы полученных прогнозов. Дайте им интерпретации. 13. Проверьте значимость в целом полученного уравнения регрессии по критерию Фишера. Значение Вероятность — уровень значимости Степени_свободы1 — число степеней свободы числителя, равно 1 (т.к. один фактор); Степени_свободы2 — число степеней свободы знаменателя, для парной регрессии равно 14. Вычислите доверительные интервалы параметров линейной регрессии. 15. Постройте прогноз среднего значения показателя и точечный прогноз значения 16. Вычислите стандартные ошибки прогноза функции регрессии и индивидуального значения и доверительные интервалы полученных прогнозов. 17. Получите результаты регрессионного анализа с помощью Пакета Анализа (Сервис/Анализ данных … Регрессия |Tools/Data Analysis …Regression). Пакет анализа, при необходимости, может быть активирован в пункте Надстройки меню Сервис. В бланке запроса этой процедуры поля Входной интервал y, Входной интервал x, Константа имеют тот же смысл, что и для функции LINEST /ЛИНЕЙН. В поле Метки поставьте флажок, если первая строка в указанном диапазоне данных содержит названия столбцов. Поставьте флажок в полях Остатки, График остатков, График подбора для того, чтобы получить соответствующую дополнительную информацию. 18. Проведите расчеты для второго фактора. Проанализируйте результаты и сделайте вывод: какой фактор лучше использовать для описания показателя и построения прогнозов.
|

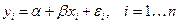 ,
,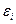 взаимно независимы и нормально распределены с нулевым математическим ожиданием и дисперсией
взаимно независимы и нормально распределены с нулевым математическим ожиданием и дисперсией  .
.
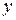 от первого фактора
от первого фактора 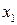 .
.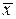 и
и  (функция СРЗНАЧ);
(функция СРЗНАЧ);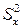 и
и 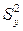 (функция ДИСПР);
(функция ДИСПР);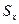 и
и 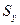 (функция СТАНДОТКЛОНП);
(функция СТАНДОТКЛОНП); (функция ПИРСОН или КОРРЕЛ).
(функция ПИРСОН или КОРРЕЛ).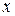 ;
;
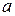
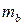 коэффициента
коэффициента 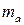 коэффициента
коэффициента 
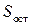
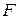 - статистики
- статистики
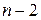
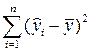
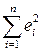
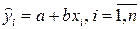 .
.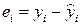 .
.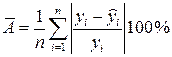 .
.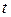 - статистик коэффициентов выборочной регрессии. Проверьте статистическую значимость полученных значений коэффициентов регрессии и коэффициента корреляции. Табличные значения определите с помощью функции СТЬЮДРАСПОБР. Аргументы этой функции:
- статистик коэффициентов выборочной регрессии. Проверьте статистическую значимость полученных значений коэффициентов регрессии и коэффициента корреляции. Табличные значения определите с помощью функции СТЬЮДРАСПОБР. Аргументы этой функции: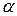 (можно принять равным 0,05, т.е. 5%);
(можно принять равным 0,05, т.е. 5%); — число наблюдений.
— число наблюдений.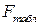 определите с помощью функции FРАСПОБР. Аргументы этой функции:
определите с помощью функции FРАСПОБР. Аргументы этой функции: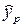 при значении фактора
при значении фактора 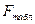 можно определить с помощью функции FРАСПОБР/FINV. Аргументы этой функции:
можно определить с помощью функции FРАСПОБР/FINV. Аргументы этой функции: , можно принять равным 0,05 (т.е. 5%);
, можно принять равным 0,05 (т.е. 5%); , где
, где  — число наблюдений.
— число наблюдений.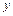 при значении
при значении 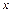 в 3 раза больше, чем среднее значение
в 3 раза больше, чем среднее значение  .
.


