Укрупнение.

При декомпозиции мы разделили задачу на максимальное количество подзадач. Однако, это совсем не обязательно приводит к эффективному параллельному алгоритму.

Во-первых, эффективность снижается за счет затрат на коммуникации. Как правило, процессор не может одновременно выполнять вычисления и обмениваться данными. Поскольку нашей задачей, как правило, являются вычисления, общая производительность может быть повышена за счет сокращения объема передаваемых данных. Менее очевидным способом повышения эффективности является сокращение количества обменов, даже при неизменном объеме передаваемых данных. Это происходит в результате сокращения накладных расходов.

Во вторых, на производительность влияют затраты на создание задач. При большом количестве малых задач эти затраты становятся значительными.

 

 

Рассмотрим пример сокращения затрат на коммуникации за счет так называемого эффекта отношения объема к поверхности. Это метод конечных разностей. В варианте а) задача разбита на 8х8=64 подзадачи, каждый из которых отвечает за 1 точку, имеются 4 связи с другими задачами и передаются и принимаются по 4 значения, 64х4=256 связей и 64х4=256 значений. В варианте б) имеются 4 подзадачи, отвечающие за 16 точек каждая. Количество коммуникаций равно 4х4=16, объем переданных данных – 4х16 = 64. Таким образом, видно, что количество переданных данных пропорционально «поверхности» субдомена, а количество вычислений – его «объему». В 2-мерной проблеме «поверхность» растет пропорционально размеру задачи, а «объем» - пропорционально квадрату размера. Этот эффект часто встречается при доменной декомпозиции. Следствием этого эффекта является то, что, как правило, более эффективными являются многомерная декомпозиция, как дающая решения с минимальной поверхностью при заданном объеме. Следовательно, с точки зрения эффективности следует увеличить зернистость по всем измерениям, а не сократить количество изменений.

На этом же этапе используются другие методы повышения производительности. Вспомним задачу суммирования. Рассмотрим вариант, при котором полученная сумма должна быть передана всем узлам, участвующим в вычислениях.

 

 

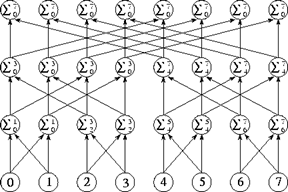
Простым алгоритмом является использование дерева или массива для выполнения вычислений и затем передачи вычисленной суммы. Таким образом, вся операция займет 2*(N-1) или 2*log N шагов соответственно. Эти алгоритмы оптимальны в том смысле, что не выполняются никакие излишние вычисления или коммуникации. Однако, можно использовать другие алгоритмы, выполняющиеся за меньшее время, хотя и за счет дополнительных, избыточных вычислений.

1-й вариант – это использование кольца вместо массива таким образом, что каждый процессор накапливает частичную сумму, и спустя N-1 шагов каждый процессор содержит окончательную сумму. Следовательно, за счет избыточных (N-1)² вычислений и (N-1)² коммуникаций, алгоритм завершается за N-1 шагов.

Аналогично можно модифицировать алгоритм на основе дерева. Выполнение множества параллельных суммирований позволяет завершить алгоритм за log N шагов. Можно ожидать, что это потребует также N² излишних суммирований и коммуникаций. Однако в данном случае имеется решение, которое позволяет ограничится N log N операций. Для этого используется структура, называемая «бабочкой»:

 

 

Здесь на каждом из log N шагов каждая задача принимает данные от 2-х других, выполняющих вычисление и передает данные 2-м другим задачам для следующего шага.

В ходе укрупнения надо избегать излишних ограничений в масштабируемости. Так, можно применять 1-мерную декомпозицию, мотивируя это тем, что количество процессоров в реальном компьютере не требует более глубокой декомпозиции. Однако, такая стратегия приводит к плохо масштабируемому решению. Если программа должна быть переносимой и масштабируемой, то при проектировании очень существенна возможность создавать переменное число задач. Это также полезно при настройке производительности для конкретного компьютера. Например, если задача часто блокируется ожиданием удаленных данных, то на стадии распределения можно назначить несколько задач одному процессору. Тогда во время ожидания одной задачей результатов обмена может выполняться другая. Это называется перекрытием вычислений и коммуникаций.

Вообще оптимальное количество задач – это не обязательно большое. Есть ряд критериев, определяющих оптимальное количество в каждом конкретном случае. Чего НАДО избегать, так это излишних ограничений.

До сих пор мы определяли стратегию укрупнения, исходя исключительно из соображений эффективности и гибкости. Другим важным аргументом может быть снижение затрат на разработку (особенно переработку существующего последовательного кода). С этой точки зрения, наиболее привлекательными оказываются стратегии, не связанные со значительной переделкой кода. Например, в случае многомерной решетки может оказаться полезным избегать декомпозиции в нескольких измерениях, если это дает возможность использовать существующий код.

Часто разработанный параллельный алгоритм должен выполняться как часть большей системы. В этом случае следует учитывать организацию данных, требованию и выделению другой компонентами системы. Допустим, оптимальный алгоритм для некоторого компонента предполагает декомпозицию по 3-м измерениям. В то же время, предыдущий этап выдает данные, разбитые по 2-м измерениям. Следовательно, требуется изменить декомпозицию либо 1 либо 2 этапа, либо использовать явное реструктурирование данных. Сравнение таких вариантов требует количественной оценки.

Итак, укрупнение используют:

- когда полученные в результате декомпозиции задачи не могут выполняться одновременно;

- чтобы увеличить зернистость вычислений и коммуникаций;

- чтобы снизить затраты на разработку, иногда ценой снижения параллельности.

 

Следовательно, контрольные вопросы, требующие ответа по окончанию этапа укрупнения:

1. снижает ли укрупнение затраты на коммуникации (за счет увеличения локальности)? Если нет, проанализируйте альтернативные стратегии укрупения с точки зрения достижения этой цели.

2. Если при укрупнении дублируются коммуникации, убедились ли вы, что преимущества этого перевешивают недостатки, для предписанного диапазона размерности задачи и количества процессоров?

3. Если при укрупнении дублируются данные, убедились ли вы, что это не снижает масштабируемость алгоритма, ограничения диапазона размерности проблемы или число процессоров?

4. Получаются ли при укрупнении задачи со сходными затратами на вычисления и коммуникации? Чем больше размер задач, полученных при укрупнении, тем это важнее. Если на процессор приходится 1 задача, они должны быть практически идентичны по затратам.

5. Масштабируется ли число задач с увеличением числа процессоров? Если нет, то проблема большей размерности не удается решить даже на большем компьютере.

6. Если при укрупнении были исключены некоторые возможности параллельного выполнения, убедились ли вы, что осталось достаточно возможностей параллельного выполнения для текущих и перспективных компьютеров? Алгоритм с недостаточной параллельностью может быть все же самым эффективным, это определяется количественным анализом.

7. Можно ли еще уменьшить количество задач, не снижая масштабируемость, не увеличивая затраты на программирование и не внося неравнозначности нагрузки? При прочих равных условиях алгоритм с меньшим числом задач обычно проще и эффективнее.

8. Если вы преобразуете существующую последовательную программу, учли ли вы затраты на переделку кода? Если они слишком высоки, можно применить другие стратегии укрупнения. Если последние дают неэффективные алгоритмы, следовательно, проводят количественную оценку и сравнение с затратами.