Вычисление коэффициентов ассоциации и контингенции
Коэффициент ассоциации: Коэффициент контингенции:
Коэффициент взаимной сопряженности Пирсона: Коэффициент взаимной сопряженности Чупрова:
Таблица 2 Вспомогательная таблица для расчета коэффициента взаимной сопряженности
Коэффициент корреляции рангов (коэффициент Спирмена): где n - число наблюдений (число пар рангов).
Ранговый коэффициент корреляции Кендалла: где n - число наблюдений (число пар рангов); S – сумма разностей между числом последовательностей и числом инверсий по второму признаку.
Коэффициент корреляции знаков Фехнера: где с – число совпадений отклонений ( н – число несовпадений отклонений ( (с+н) – общее количество значений признака.
Коэффициент конкордации: где m- количество факторов, n – число наблюдений; S – отклонение суммы квадратов рангов от средней квадратов рангов.
Пример I. Исследуем связь между успеваемостью студентов и обеспеченностью учебно-методической литературой по курсу «Теория статистики». Результаты обследования характеризуются следующими данными: Таблица 3
|

 (1)
(1)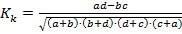 (2)
(2) (3)
(3) , где (4)
, где (4)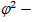 показатель взаимной сопряженности;
показатель взаимной сопряженности;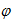 - определяется как сумма отношений квадратов частот каждой клетки таблицы к произведению итоговых частот, соответствующего столбца и строки. Вычитая из этой суммы «1» получим величину
- определяется как сумма отношений квадратов частот каждой клетки таблицы к произведению итоговых частот, соответствующего столбца и строки. Вычитая из этой суммы «1» получим величину 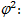
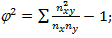 (5)
(5)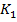 - число значений (групп) первого признака;
- число значений (групп) первого признака;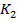 - число значений (групп) второго признака.
- число значений (групп) второго признака.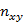
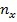
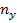
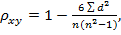 (6)
(6)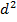 - квадраты разности рангов;
- квадраты разности рангов; (7)
(7)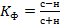 , (8)
, (8)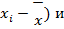 (
(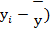 по знаку;
по знаку;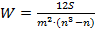 , (9)
, (9)


