Изотермы адсорбции.
Для данной пары адсорбент-адсорбат величины адсорбции a или Г - определяется двумя основными термодинамическими параметрами состояния: температурой T и давлением p при газообразном адсорбате или температурой T и концентрацией C при адсорбции из растворов. Все три величины - адсорбция a, температура T и давление p (концентрация C) - связаны функциональной зависимостью, называемой термическим уравнением обратимой сорбции: f(a,p,T)=0, или В конкретных случаях эти уравнения имеют различный вид. В теории адсорбции часто рассматривают адсорбционное равновесие при условии, что один из параметров, входящих в термическое уравнение, поддерживают постоянным. Адсорбция, если она выражена не как избыток, а как полное содержание всегда возрастает с повышением равновесного давления (концентрации). Так как адсорбция - процесс экзотермический, то при повышении температуры величина адсорбции снижается (рис. 2.5.4, на котором Уравнения, связывающее величину адсорбции с температурой при постоянном равновесном давлении a=f
Рис.2.5.4. Основные виды кривых адсорбционного равновесия: изотермы (Т=const), изобары (р=const) или изопикны (если С=const), изостеры (а=const). Теория адсорбционного равновесия ставит задачей на базе определенной модели процесса адсорбции составить ее математическое описание. Уравнение в идеале должно количественно описывать зависимость равновесной величины адсорбции от концентрации адсорбата в объемной фазе при различных температурах, а также правильно предсказывать изменение теплоты адсорбции от заполнения адсорбента. Наиболее часто при этом находят уравнение изотермы адсорбции. Форма изотермы адсорбции на твердых телах зависит от многих параметров: свойств адсорбента и адсорбата. взаимодействие адсорбент-адсорбат, взаимодействия молекул адсорбата между собой в газовой фазе и в адсорбированном состоянии. В области малых давлений (концентраций) и соответствующих им малых заполнений поверхности взаимодействие между молекулами адсорбата незначительно, и зависимость a=f A = kp, или a=kC (2.5.1) Величина адсорбции пропорциональна концентрации адсорбтива в растворе. Коэффициент пропорциональности k - коэффициент Генри - является мерой интенсивности адсорбции. При больших давлениях (концентрациях) и соответствующих им больших заполнениях адсорбцию часто выражают эмпирическим уравнением Фрейндлиха:
где Уравнение Фрейндлиха применимо для адсорбции недиссоциируемых или слабо диссоциируемых веществ, когда вещества адсорбируются в виде целых молекул. Такие явления происходят при молекулярной адсорбции, которая характеризуется следующим правилом: чем лучше данный растворитель смачивает твердую поверхность, тем меньше адсорбция молекул растворенного вещества из растворителя на данной поверхности, и наоборот. Уравнение Фрейндлиха (2.5.2) нельзя применять при очень малых и очень больших концентрациях, когда кривая зависимости адсорбции от концентрации принимает вид прямой линии и показатель 1/n становится равным нулю или единице. В логарифмированном виде уравнение Фрейндлиха представляет собой прямую (рис. 2.5.5). По отрезку, отсекаемому прямой на оси ординат, определяем значение lnк, а по тангенсу угла наклона прямой к оси ординат - значение 1 /п.
Первое теоретическое уравнение изотермы адсорбции было предложено И. Лэнгмюром в 1914 г. Это уравнение до сих пор не потеряло своего значения. Теория Лэнгмюра основана на трех основных предположениях: 1.Адсорбция происходит на дискретных адсорбционных центрах, которые могут иметь различную природу. 2.При адсорбции соблюдается строгое стехиометрическое условие - на одном центре адсорбируется одна молекула. (Это означает, что по Лэнгмюру на поверхности может образовываться только один адсорбционный слой, называемый мономолекулярным.) 3.Адсорбционные центры энергетически однородны и независимы, т.е. адсорбция на одном центре не влияет на адсорбцию на других центрах. (Это означает, что дифференциальная теплота адсорбции постоянна, и, что силами взаимодействия адсорбированных молекул между собой можно пренебречь.) На основе этих трех положений можно различными путями получить уравнение изотермы адсорбции. Молекулы в газовой фазе находятся в состоянии теплового движения. Они могут сталкиваться с адсорбционными центрами и адсорбироваться на них. Скорость этого процесса Поэтому Адсорбированные молекулы колеблются около центров. Вследствие флуктуаций энергии некоторые адсорбированные молекулы отрываются от центров и возвращаются в газовую фазу. Этот процесс называется десорбцией. Скорость десорбции пропорциональна числу адсорбированных молекул:
При равновесии
Отсюда, вводя обозначения: где
Полученное уравнение изотермы адсорбции называется уравнением Лэнгмюра. Константа b - константа адсорбционного равновесия называется адсорбционным коэффициентом. Если измерить поверхность поглощающего вещества (порошки, пористые материалы и др.) затруднительно, то адсорбцию рассчитывают на единицу массы, т. е. на 1 г адсорбента, принимая, что масса пропорциональна его поверхности. Если при постоянной температуре на оси абсцисс откладывать величину давления газа, а на оси ординат - количество адсорбированного вещества, то можно построить изотерму адсорбции. На процесс адсорбции давление влияет по-разному (рис.2.5.6). Адсорбция быстро возрастает в области малых давлений. Количество адсорбированного вещества при дальнейшем повышении давления увеличивается в меньшей степени. При достаточно высоких давлениях изотермы адсорбции стремятся к прямой, параллельной оси абсцисс. Это означает, что при достижении насыщения дальнейшее повышение давления не влияет на количество адсорбированного вещества.
Крутой подъем начальной части изотермы свидетельствует о том, что небольшое увеличение концентрации адсорбируемого вещества сопровождается значительным увеличением адсорбции. При дальнейшем повышении концентрации рост адсорбции замедляется и затем приостанавливается: адсорбция достигает максимума. Как и все обратимые процессы, адсорбция подчиняется принципу подвижного равновесия. Так, при повышении температуры равновесие сдвигается в сторону эндотермического процесса. Это означает, что с повышением температуры равновесие сдвигается в сторону десорбции и количество адсорбированного вещества уменьшается. С повышением давления, как правило, увеличивается количество адсорбированного газа. Теория адсорбции «БЭТ». С.Брунауэр, П.Эммет и Э.Теллер отказались от второго допущения И.Лэнгмюра, приводящего к мономолекулярной адсорбции. Для случая, когда адсорбтив находится при температуре ниже критической, т.е. в парообразном состоянии, эти авторы разработали теорию полимолекулярной адсорбции, имеющую большое практическое значение. С. Брунауэр проанализировал многочисленные реальные изотермы адсорбции и предложил их классификацию. Согласно этой классификации можно выделить пять основных типов изотерм адсорбции, изображенных на рисунке 2.5.7.
Рис.2.5.7. Типы изотерм адсорбции по классификации Брунауэра.
Изотерма типа I отражает мономолекулярную адсорбцию (описываемая уравнением Лэнгмюра). Изотермы типа II и III обычно связывают с образованием при адсорбции многих слоев, т.е. полимолекулярной адсорбцией. Различие между этими изотермами обусловлены различным соотношением энергии взаимодействия адсорбат-адсорбент и адсорбат-адсорбат. Изотермы типа IV и V отличаются от изотерм II и III тем, что в первых случаях адсорбция возрастает бесконечно при приближении давления пара к давлению насыщения, а в других случаях имеет место конечная адсорбция при давлениях насыщения. Изотермы типа II и III обычно характерны для адсорбции на непористом адсорбенте, а типа IV и V - на пористом твердом теле. Все пять типов изотерм адсорбции описываются теорией полимолекулярной адсорбции "БЭТ", названной так по начальным буквам фамилии ее авторов. Теория БЭТ сохраняет Лэнгмюровскую концепцию о динамическом характере адсорбции. Адсорбция считается полислойной. Молекулы первого слоя адсорбируются на поверхности адсорбента в результате межмолекулярного взаимодействия адсорбент-адсорбат. Каждая адсорбированная молекула первого адсорбционного слоя может в свою очередь являться центром адсорбции молекул второго слоя, те - молекул третьего и т.д. Так формируются второй и последующие слои. Начало образования второго и последующих слоев возможно и при незаконченном первом. Каждый адсорбционный слой находится в динамическом равновесии с окружающей средой и соседними слоями. Если обозначить через
Составив уравнение адсорбционного равновесия для каждого слоя, и просуммировав их, авторы теории получили, в конечном счете, уравнение изотермы адсорбции:
В этом уравнении Уравнение изотермы адсорбции "БЭТ" широко используется для определения величины удельной поверхности адсорбентов. Изотерма адсорбции в координатах
где N - постоянная Авогадро,
Стандартной методикой для определения удельной поверхности адсорбентов принято считать измерение изотермы адсорбции азота при
Вопросы для закрепления.
П Р И Л О Ж Е Н И Е
|

 (Г,с,Т)=0.
(Г,с,Т)=0. ).
). или постоянной равновесной концентрации Г=
или постоянной равновесной концентрации Г=  носит название соответственно изобары и изопикны адсорбции (рис.2.5.4,
носит название соответственно изобары и изопикны адсорбции (рис.2.5.4,  ). Уравнение вида p=
). Уравнение вида p=  (изостера адсорбции) связывает равновесное давление с температурой при постоянном адсорбированным количестве (рис.2.5.4.).
(изостера адсорбции) связывает равновесное давление с температурой при постоянном адсорбированным количестве (рис.2.5.4.).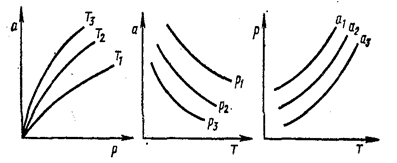
 сводится к простейшей форме, называемой законом Генри:
сводится к простейшей форме, называемой законом Генри: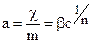 , (2.5.2)
, (2.5.2)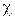 -количество адсорбированного вещества, m-масса адсорбента,
-количество адсорбированного вещества, m-масса адсорбента, 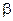 и n –константы, характерные для каждой адсорбированной системы, причем 1/n всегда правильная дробь (0<1/n<1). По Г. Фрейндлиху n не зависит от заполнения, хотя это утверждение не вполне точно. Этим эмпирическим уравнением часто пользуются для ориентировочных расчетов адсорбции.
и n –константы, характерные для каждой адсорбированной системы, причем 1/n всегда правильная дробь (0<1/n<1). По Г. Фрейндлиху n не зависит от заполнения, хотя это утверждение не вполне точно. Этим эмпирическим уравнением часто пользуются для ориентировочных расчетов адсорбции.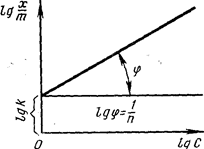
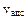 (т.е. число молекул, адсорбирующихся за единицу времени) пропорциональна давлению газа и числу свободных центров на поверхности. Если общее число центров a, то при адсорбции, равной a, число свободных центров равно (am-а).
(т.е. число молекул, адсорбирующихся за единицу времени) пропорциональна давлению газа и числу свободных центров на поверхности. Если общее число центров a, то при адсорбции, равной a, число свободных центров равно (am-а). .
.
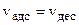 или
или (2.5.3)
(2.5.3) ,
, - относительное заполнение поверхности) получим:
- относительное заполнение поверхности) получим: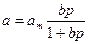 , или
, или 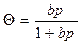 . (2.5.4)
. (2.5.4)

 и т.д. площади поверхности адсорбента, покрытые 0 1 2 слоями адсорбированных молекул, то вся площадь поверхности адсорбента будет равна сумме площадей с разным числом слоев
и т.д. площади поверхности адсорбента, покрытые 0 1 2 слоями адсорбированных молекул, то вся площадь поверхности адсорбента будет равна сумме площадей с разным числом слоев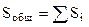

 -величина адсорбции, соответствующая заполнению поверхности адсорбента мономолекулярным слоем адсорбата ("емкость монослоя") с - константа, равная
-величина адсорбции, соответствующая заполнению поверхности адсорбента мономолекулярным слоем адсорбата ("емкость монослоя") с - константа, равная  , где
, где 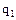 -теплота адсорбции в первом слое,
-теплота адсорбции в первом слое, 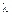 -теплота адсорбции во всех слоях, равная теплоте конденсации. При малых относительных давлениях когда p<<
-теплота адсорбции во всех слоях, равная теплоте конденсации. При малых относительных давлениях когда p<< 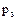 последнее уравнение преобразуется в уравнение Лэнгмюра. Таким образом, изотерма Лэнгмюра может рассматриваться как частный случай уравнения "БЭТ".
последнее уравнение преобразуется в уравнение Лэнгмюра. Таким образом, изотерма Лэнгмюра может рассматриваться как частный случай уравнения "БЭТ".
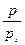 выражается прямой линией (рис. 2.5.8), отсекающей на оси ординат отрезок равный
выражается прямой линией (рис. 2.5.8), отсекающей на оси ординат отрезок равный 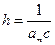 , а тангенс угла наклона к оси абсцисс равен
, а тангенс угла наклона к оси абсцисс равен 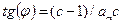 . Из этих значений можно найти величину
. Из этих значений можно найти величину 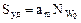 ,
,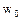 - площадь, приходящаяся на одну молекулу адсорбата в первом адсорбционном слое.
- площадь, приходящаяся на одну молекулу адсорбата в первом адсорбционном слое.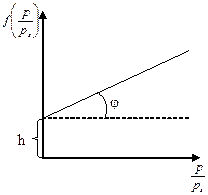
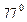 K. В этом случае
K. В этом случае  =0,162 нм.
=0,162 нм.


