Механика 5 Законы сохранения в механике
Теорема об изменении и закон сохранения импульса материальной точки: дифференциальная форма теоремы об изменении импульса материальной точки: дифференциал импульса материальной точки равен элементарному импульсу силы, приложенной к ней интегральная формулировка теоремы об изменения импульса материальной точки Закон сохранения импульса материальной точки: если равнодействующая сил, приложенных к материальной точке равна нулю, то импульс материальной точки остаётся постоянным Моментом силы относительно произвольной точки О называют вектор Момент импульса материальной точки: Теорема об изменении момента импульса материальной точки в дифференциальной форме: производная по времени от момента импульса материальной точки равна сумме моментов сил, действующих на материальную точку Теорема об изменении момента импульса материальной точки в интегральной форме: Закон сохранения момента импульса материальной точки: если момент сил, действующих на материальную точку равен нулю Сумму кинетической и потенциальной энергий материальной точки называют полной механической энергией материальной точки. Закон сохранения полной механической энергии: полная механическая энергия материальной точки сохраняется, если на материальную точку действуют консервативные силы Радиус-вектор центра масс: для системы материальных точек для материального тела для системы материальных тел Координаты центра масс: для системы материальных точек для материального тела для системы материальных тел Скорость и ускорение центра масс: для системы материальных точек для материального тела для системы материальных тел Проекции скорости и ускорения центра масс:
для системы материальных точек
для материального тела
для системы материальных тел
Теорема об изменении импульса механической системы в дифференциальной форме: первая производная по времени от импульса механической системы равна главному вектору внешних сил для системы материальных точек для материального тела для системы материальных тел Закон сохранения импульса механической системы: если механическая система является замкнутой ( Закон сохранения импульса в случае абсолютно упругого столкновения двух тел: При неупругом ударе, когда тела слипаются после соударения, их общая скорость Теорема об изменении момента импульса (кинетического момента) механической системы тел:
|

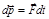 ;
;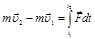 .
. если
если 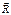 =0, то
=0, то 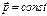 .
.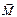 , определяемый формулой
, определяемый формулой 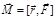 , где
, где 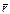 – вектор, проведённый из точки О в точку приложения силы.
– вектор, проведённый из точки О в точку приложения силы.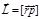 .
.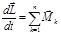 .
.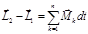 .
.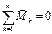 , то момент импульса материальной точки сохраняется
, то момент импульса материальной точки сохраняется 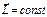 .
.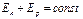 .
.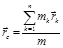 ;
;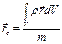 ;
;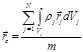 .
.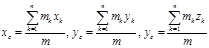 ;
;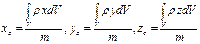 ;
;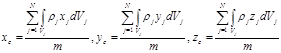 .
.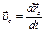 ,
, 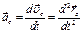
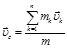 ,
, 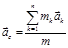 ;
;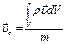 ,
, 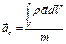 ;
;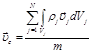 ,
, 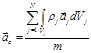 .
.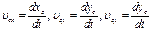 ;
;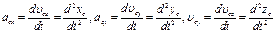 ;
;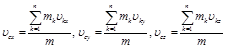 ;
;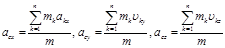 ;
;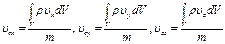 ;
;  ;
;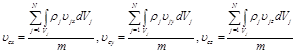 ;
; .
.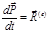 , где:
, где: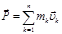 – импульс системы материальных точек;
– импульс системы материальных точек; 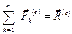 – главный вектор внешних сил системы материальных точек;
– главный вектор внешних сил системы материальных точек;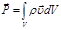 – импульс материального тела;
– импульс материального тела; 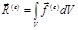 – главный вектор внешних сил материального тела;
– главный вектор внешних сил материального тела;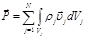 – импульс материального тела;
– импульс материального тела; 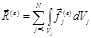 – главный вектор внешних сил материального тела.
– главный вектор внешних сил материального тела.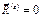 ), то её импульс сохраняется (
), то её импульс сохраняется (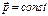 ).
).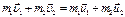 , где
, где 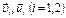 – скорости тел 1 и 2 до и после соударений соответственно.
– скорости тел 1 и 2 до и после соударений соответственно.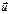 становится равной
становится равной 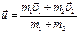 .
.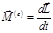 .
.


