Ф1.5.3 Закон сохранения момента импульса
Ф1.5.3-1
| Человек сидит в центре вращающейся по инерции вокруг вертикальной оси карусели и держит в руках длинный шест за его середину. Если он повернет шест из вертикального положения в горизонтальное, то частота вращения в конечном состоянии
| 1. увеличится
2. не изменится
3. уменьшится*
|  Поскольку проекции моментов внешних сил на ось вращения равны нулю, то сумма проекций моментов импульса системы сохраняется (под системой понимаем карусель – 1, человек – 2, шест – 3): Поскольку проекции моментов внешних сил на ось вращения равны нулю, то сумма проекций моментов импульса системы сохраняется (под системой понимаем карусель – 1, человек – 2, шест – 3):  , где I – момент инерции системы, ω; – угловая скорость системы. Тогда: , где I – момент инерции системы, ω; – угловая скорость системы. Тогда: 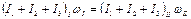 . Моменты инерции карусели и человека не изменяются, моменты инерции тонкого стержня . Моменты инерции карусели и человека не изменяются, моменты инерции тонкого стержня 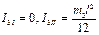 . После подстановки получаем: . После подстановки получаем: 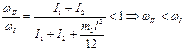 . Следовательно, угловая скорость и частота вращения уменьшаются. Ответ: 3 . Следовательно, угловая скорость и частота вращения уменьшаются. Ответ: 3
| Ф1.5.3-2
Тело массой m падает вертикально со скоростью  на горизонтальную опору и упруго отскакивает от неё. Импульс, полученный опорой, равен … на горизонтальную опору и упруго отскакивает от неё. Импульс, полученный опорой, равен …
| 1.  2.
2. 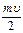 3.
3. 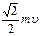 4.
4.  5.
5. 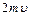 * *
| 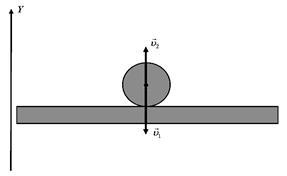 Изменение импульса тела Изменение импульса тела 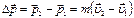 . При упругом ударе импульс тела меняет своё направление на противоположное, модуль импульса тела сохраняется, то есть . При упругом ударе импульс тела меняет своё направление на противоположное, модуль импульса тела сохраняется, то есть  . Поэтому . Поэтому 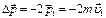 . В соответствии с законом сохранения импульса системы изменение импульса горизонтальной опоры . В соответствии с законом сохранения импульса системы изменение импульса горизонтальной опоры  . В проекции на ось Y: . В проекции на ось Y: 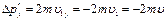 . Модуль изменения импульса опоры или импульс, полученный опорой, равен: . Модуль изменения импульса опоры или импульс, полученный опорой, равен: 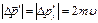 . Ответ: 5 . Ответ: 5
| Ф1.5.3-3
Невесомая доска покоится на двух опорах. Правая опора делит длину доски в соотношении 1: 3. На ее правый конец падает тело массой m2=1 кг, теряя при ударе всю свою скорость. Если после удара тело массой m1=2 кг начинает двигаться со скоростью V1, то скорость V2 равна…

| 1: 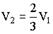 *
2: *
2: 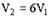 3:
3:  4:
4: 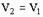
| Поскольку проекции моментов внешних сил, действующих на механическую систему (под механической системой будем понимать грузы массами m 1, m 2 и невесомая доска), на ось вращения равны нулю, то сумма проекций моментов импульса системы на ось вращения будет сохраняться (момент импульса доски равен нулю, т.к. её масса равна нулю – она невесома): 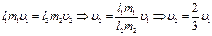 . Ответ: 1 . Ответ: 1
| Ф1.5.3-9
Планета массой m движется по эллиптической орбите, в одном из фокусов которой находится звезда массой М.
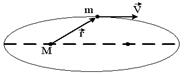 Если
Если  - радиус-вектор планеты, то справедливы утверждения: - радиус-вектор планеты, то справедливы утверждения:
| 1. Момент силы тяготения, действующей на планету, относительно центра звезды, не равен нулю.
2. Момент импульса планеты относительно центра звезды при движении по орбите не изменяется.*
3. Для момента импульса планеты относительно центра звезды справедливо выражение L = mVr
| 1. Момент силы тяготения, действующей на планету, относительно центра звезды, равен нулю, так как 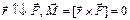 .
2. Момент импульса планеты относительно центра звезды при движении по орбите не изменяется. Поскольку согласно теореме об изменении момента импульса .
2. Момент импульса планеты относительно центра звезды при движении по орбите не изменяется. Поскольку согласно теореме об изменении момента импульса  и и  , то , то 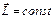 .
3. Для момента импульса планеты относительно центра звезды не справедливо выражение L = mVr. Справедливым является соотношение .
3. Для момента импульса планеты относительно центра звезды не справедливо выражение L = mVr. Справедливым является соотношение  . Ответ: 2 . Ответ: 2
|

Вычисление основной дактилоскопической формулы Вычислением основной дактоформулы обычно занимается следователь. Для этого все десять пальцев разбиваются на пять пар...
|

Расчетные и графические задания Равновесный объем - это объем, определяемый равенством спроса и предложения...
|

Кардиналистский и ординалистский подходы Кардиналистский (количественный подход) к анализу полезности основан на представлении о возможности измерения различных благ в условных единицах полезности...
|

Обзор компонентов Multisim Компоненты – это основа любой схемы, это все элементы, из которых она состоит. Multisim оперирует с двумя категориями...
|
Характерные черты официально-делового стиля Наиболее характерными чертами официально-делового стиля являются:
• лаконичность...
Этапы и алгоритм решения педагогической задачи Технология решения педагогической задачи, так же как и любая другая педагогическая технология должна соответствовать критериям концептуальности, системности, эффективности и воспроизводимости...
Понятие и структура педагогической техники Педагогическая техника представляет собой важнейший инструмент педагогической технологии, поскольку обеспечивает учителю и воспитателю возможность добиться гармонии между содержанием профессиональной деятельности и ее внешним проявлением...
|
Анализ микросреды предприятия Анализ микросреды направлен на анализ состояния тех составляющих внешней среды, с которыми предприятие находится в непосредственном взаимодействии...
Типы конфликтных личностей (Дж. Скотт) Дж. Г. Скотт опирается на типологию Р. М. Брансом, но дополняет её. Они убеждены в своей абсолютной правоте и хотят, чтобы...
Гносеологический оптимизм, скептицизм, агностицизм.разновидности агностицизма Позицию Агностицизм защищает и критический реализм. Один из главных представителей этого направления...
|
|