Лабораторна робота № 2. МЕТА РОБОТИ: визначити характер закономірності радіоактивного розпаду.
ВИВЧЕННЯ ЗАКОНОМІРНОСТЕЙ РАДІОАКТИВНОГО РОЗПАДУ МЕТА РОБОТИ: визначити характер закономірності радіоактивного розпаду. ЗАВДАННЯ: 1. Отримати статистичні дані, що характеризують розпад ядер у радіоактивному препараті; 2. Порівняти отримані статистичні дані розпаду ядер з теоретичною кривою, яка характеризує статистичний процес; 3. Визначити характер закономірності радіоактивного розпаду. ТЕОРЕТИЧНІ ВІДОМОСТІ. Розділяють два типи фізичних закономірностей: динамічні і статистичні. Динамічні закономірності дають однозначну картину явищ, тобто знаючи умови, що характеризують систему в деякий початковий момент часу, можна передбачити її стан в будь-який момент часу. Статистичні закономірності встановлюють зв'язок між явищами, які не носять однозначний характер. Ці закономірності проявляють себе тоді, коли випадкові явища протікають незалежно одне від одного. При дослідженні статистичних закономірностей важливу роль має статистична похибка. Вона пояснюється наявністю флуктуацій у вимірюваній величини біля її середнього значення. Радіоактивний розпад ядер носить імовірний характер. При цьому імовірність розпаду ядра Р пропорційна інтервалу часу Dt і може бути представлена у вигляді:
де l - постійна розпаду, що визначається властивостями ядра. Завдяки спонтанного розпаду ядер закон радіоактивного розпаду має вигляд:
No – число радіоактивних ядер в момент часу t = 0; N(t) – число радіоактивних ядер в момент часу t. Закон радіоактивного розпаду носить статистичний характер і виконується точно тільки для великих чисел No і N. Статистичний характер закону можна перевірити експериментально за методикою, запропонованою Резерфордом і Гейгером. Вони підраховували число частинок, які випромінював радіоактивний препарат малої інтенсивності за однакові проміжки часу. Далі за результатами експерименту визначалась загальна кількість періодів (проміжків) часу, за який випромінювалось однакове число частинок і будувався графік залежності числа інтервалів N від числа зареєстрованих часток n, тобто Nек(n).Отримана під час експерименту залежність Nек(n) порівнювалась з аналогічною теоретичною залежністю, описаною статистичною формулою Пуассона. Формула Пуассона описує статистичні процеси, що носять дискретний і незалежний характер. З її допомогою можна передбачити імовірність Р(ni) певної події (поява ni частинок за проміжок часу Dt=1 с). Формула Пуассона має вигляд:
де
де, ni – число імпульсів за i -й проміжок часу, “ i ” змінюється від 1 до К, де К – кількість інтервалів (проміжків часу) в досліді. Користуючись формулою (2) можна розрахувати теоретично скільки разів при виконанні досліду спостерігається однакове число імпульсів NТ(ni) радіоактивного розпаду. Якщо всіх інтервалів в досліді було К, то: N(ni)=P(ni)•K (4) Порівнюючи графік Nек(ni), що отримали експериментально, із графіком NT(ni) можна визначити їх подібність чи розбіжність і зробити висновок про характер закону радіоактивного розпаду. Якщо графіки збігаються в межах можливих похибок, то закон радіоактивного розпаду носить статистичний характер і імовірність певного розпаду можна визначити за формулою Пуассона (2). В цьому переконуються студенти, виконуючи дану лабораторну роботу. СКЛАДОВІ ЧАСТИНИ ЕКСПЕРИМЕНТАЛЬНОЇ УСТАНОВКИ. У даній роботі використовується наступна вимірювальна установка, що складається з: 1. джерела живлення; 2. рахункового пристрою ПСО2-4; 3. лічильника Гейгера-Мюллера в захисному кожусі; 4. радіоактивного препарату; 5. алюмінієвих пластинок. Рахунковий пристрій ПСО2-4 може визначати різні проміжки часу в межах (від 0,1 до 1000 с).
|

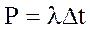 ,
,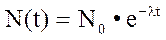 (1)
(1)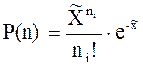 (2)
(2) – середнє число частинок, що з’являються за проміжок часу Dt=1 с.
– середнє число частинок, що з’являються за проміжок часу Dt=1 с.  (3)
(3)


