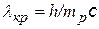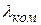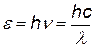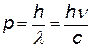Задерживающий потенциал.
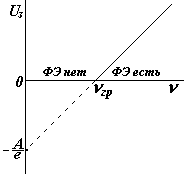
На рисунке показан график зависимости задерживающего потенциала от частоты падающего света. По графику можно найти работу выхода А, красную границу nгр , а по наклону прямой можно определить величину постоянной Планка h.
Фотоэлементы широко используются в физике и технике. Вакуумные фотоэлементы довольно громоздки и дают небольшие токи, но вследствие своей безинерционности и линейной световой характеристики они незаменимы в тех случаях, когда необходимо превратить световые сигналы в электрические без каких-либо искажений. Существование тока насыщения в фотоэлементах позволят использовать их в стабилизаторах (напряжение изменяется, а ток остается постоянным). Фотоэлементы очень часто применяют в турникетах, для подсчета движущихся изделий на конвейерах и т.п.
ЭФФЕКТ КОМПТОНА Эффектом Комптона называется рассеяние веществом электромагнитного излучения, при котором частота рассеянного излучения уменьшается по сравнению с первоначальной, и одновременно наблюдается вылет быстрых электронов (электроны отдачи). Изменение частоты оказывается различной в зависимости от угла наблюдения. Американский ученый Комптон, открывший это явление (1923 г) разработал теорию явления. Он предложил рассматривать наблюдаемое взаимодействие света с веществом как упругое столкновение частиц - фотона и электрона. Используя законы сохранения импульса и энергии, Комптон получил формулу для изменения длины волны в зависимости от угла рассеяния.. Мы не будем приводить полный вывод формулы для изменения длины волны, а запишем только законы сохранения и окончательную формулу. Так как эффект Комптона наблюдается только для фотонов с большой энергией (рентгеновские и гамма-лучи), то при вычислениях необходимо использовать формулы СТО, и вывод становится громоздким. [x]
Подставив в эти законы выражения для указанных величин, приведенные ниже, после преобразований получим:
Комптоновское рассеяние может наблюдаться и на свободном протоне, тогда следует использовать комптоновскую длину волны протона: Из формулы (¨) следует, что изменение l при различных углах рассеяния равно:
Ниже приводится таблица формул, используя которые можно получить выражение (¨) для D l. Компактное расположение формул облегчает также решение задач.
Комптоновское рассеяние наблюдается только для рентгеновских и гамма-лучей. В этом случае изменение длины волны сравнимо с длиной волны падающего излучения, и может быть измерено экспериментально. Для видимого света обнаружить эффект Комптона невозможно, т.к. максимальное изменение D l = 0,48 пм слишком мало по сравнению со средней длиной световой волны l» 500 нм = 500000 пм (зеленый свет) и перекрывается тепловым уширением спектральных линий.. Эффект Комптона доказывает, что: 1) свет имеет квантовую природу и 2) для элементарных процессов взаимодействия частиц применимы законы сохранения импульса и энергии. ЭНЕРГЕТИЧЕСКИЕ СПЕКТРЫ АТОМОВ И МОДЕЛЬ АТОМА БОРА.
|

 Уравнение Эйнштейна можно записать в виде:
Уравнение Эйнштейна можно записать в виде: 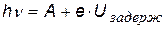 и выразить задерживающий потенциал:
и выразить задерживающий потенциал: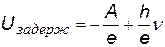
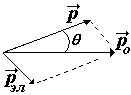
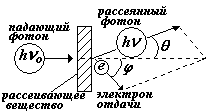 На рис. показано столкновение первоначального фотона с энергией hn о с электроном в веществе (на рис. не показан). Импульс и энергия электрона до столкновения пренебрежимо малы по сравнению с импульсом и энергией фотона, т.е. электрон можно считать свободным. (Обычно употребляется выражение «рассеяние фотона на свободном электроне»). После столкновения фотон отклоняется от первоначального направления под углом q, а его энергия уменьшается и становится равной hn. Электрон получает импульс и кинетическую энергию и летит под углом j. (электрон отдачи, угол отдачи).
На рис. показано столкновение первоначального фотона с энергией hn о с электроном в веществе (на рис. не показан). Импульс и энергия электрона до столкновения пренебрежимо малы по сравнению с импульсом и энергией фотона, т.е. электрон можно считать свободным. (Обычно употребляется выражение «рассеяние фотона на свободном электроне»). После столкновения фотон отклоняется от первоначального направления под углом q, а его энергия уменьшается и становится равной hn. Электрон получает импульс и кинетическую энергию и летит под углом j. (электрон отдачи, угол отдачи).
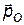 - импульс падающего фотона,
- импульс падающего фотона,
 - импульс рассеянного фотона,
- импульс рассеянного фотона,
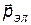 - импульс электрона.
q - угол рассеяния
- импульс электрона.
q - угол рассеяния

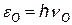 - энергия падающего фотона,
- энергия падающего фотона,
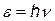 - энергия рассеянного фотона,
- энергия рассеянного фотона,
 - кинетическая энергия электрона отдачи
(электрон релятивистский).
- кинетическая энергия электрона отдачи
(электрон релятивистский).
 ¨
или
¨
или
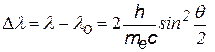
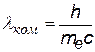 = 2,43 пм = 2,43×10-12 м
= 2,43 пм = 2,43×10-12 м