В классической физике гармоническим осциллятором называют частицу, совершающую движения по закону синуса или косинуса. Потенциальная энергия такой частицы U = кх2/2, частота колебаний 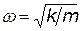 . Посмотрим, к каким результатам приведет решение уравнения Шрёдингера (a), если его применить к одномерной частице, которая обладает такой потенциальной энергией.
. Посмотрим, к каким результатам приведет решение уравнения Шрёдингера (a), если его применить к одномерной частице, которая обладает такой потенциальной энергией.
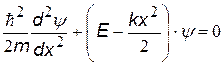
| уравнение Шрёдингера для гармонического осциллятора
Т.к. случай одномерный, оператор Лапласа
D y = d2y / dx2, потенциальная энергия U = кх2/2.
|
Мы не приводим решение этого уравнения, т.к. оно выходит далеко за рамки курса. [xv] Из решения следует, что полная энергия Е такого осциллятора квантуется:

| Полная энергия квантового осциллятора
n = 0, 1, 2,…,¥
|
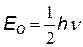 при
n = 0 при
n = 0
| Эта величина называется нулевой энергией осциллятора.
|
 По классическим представлениям при Т ® 0 К энергия должна стремиться к 0, решение уравнения Шрёдингера приводит к выводу о существовании нулевой энергии;
По классическим представлениям при Т ® 0 К энергия должна стремиться к 0, решение уравнения Шрёдингера приводит к выводу о существовании нулевой энергии;
даже при абсолютном нуле (Т = 0 К) частица имеет энергию ¹ 0.
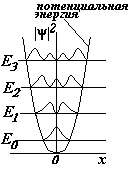
На рис. показаны плотности вероятности 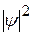 при различных энергиях Е осциллятора. Если мы спросим себя, а как ведет себя частица, ведь нам всегда хочется наглядно представить процессы. Ответ – не знаем, ведь квантовый объект имеет двойственную природу. Мы можем только сказать, что частица находится в потенциальной яме, имеет определенный набор энергий и, если ее энергия равна, например Е1, то вероятность обнаружить ее в середине ямы равна нулю. При переходе на другой уровень энергия частицы меняется дискретно, и система поглощает или испускает порцию энергии hn.
при различных энергиях Е осциллятора. Если мы спросим себя, а как ведет себя частица, ведь нам всегда хочется наглядно представить процессы. Ответ – не знаем, ведь квантовый объект имеет двойственную природу. Мы можем только сказать, что частица находится в потенциальной яме, имеет определенный набор энергий и, если ее энергия равна, например Е1, то вероятность обнаружить ее в середине ямы равна нулю. При переходе на другой уровень энергия частицы меняется дискретно, и система поглощает или испускает порцию энергии hn.
Существование нулевой энергии следует также из соотношения неопределенности. Действительно.
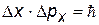
| соотношение неопределенностей
|
| D х» А
| неопределенность в координате примем равной амплитуде А колебаний
|
| D р» р = mv = mw А
| неопределенность в импульсе примем равной самому импульсу; максимальная скорость колебаний v = w А
|
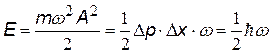
| Е - максимальная энергия гармонических колебаний (Е =кх2 /2, 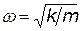 ) )
|
| | | |
Таким образом, из соотношения неопределенностей следует, что энергия осциллятора равна  .
.
Частица в одномерной потенциальной яме (ящике)
Рассмотрим частицу с массой m, находящуюся в потенциальной яме, например, электрон в металле. Чтобы иметь возможность решить уравнение Шрёдингера введем следующие упрощения.
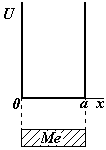 1).Частица находится в прямоугольной потенциальной яме, внутри ямы потенциальная энергия U постоянна, примем ее равной нулю = 0. Высота стенок ямы ® ¥, т.е. частица не может выйти из ямы (см.рис.).
1).Частица находится в прямоугольной потенциальной яме, внутри ямы потенциальная энергия U постоянна, примем ее равной нулю = 0. Высота стенок ямы ® ¥, т.е. частица не может выйти из ямы (см.рис.).
2). Частица может двигаться только по оси х в пределах ширины ямы а, т.е. 0£ х £ а (одномерная задача).
Запишем уравнение Шрёдингера a для частицы в виде:
 [ [
| Уравнение Шрёдингера для частицы в прямоугольной потенциальной яме
|
При решении этого уравнения нам нужно найти пси-функцию y (х) и энергию Е частицы. По форме - это уравнение колебаний. Из математики известно, что решение такого дифференциального уравненияимеет вид: 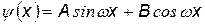 . Для нахождения коэффициентов А и В используем краевое условие
. Для нахождения коэффициентов А и В используем краевое условие 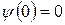 , смысл которого в том, что частица не может выйти из ямы.
, смысл которого в том, что частица не может выйти из ямы.
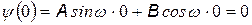
| Отсюда следует: 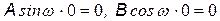 , т.к. sin 0 = 0, а cos 0 = 1 ¹ 0, то В = 0 , т.к. sin 0 = 0, а cos 0 = 1 ¹ 0, то В = 0
|
Таким образом, получаем:
 · ·
| Решение уравнения ([).
Здесь неизвестными пока остаются А и w.
|
Величину w найдем из второго краевого условия 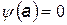


| А ¹ 0, следовательно, sinwa = 0, и значит wa = np, где
n - -целые числа. Отсюда получаем w.
|
Вторую неизвестную величину А найдем из условия нормировки.

| Смысл этого условия в том, что частица обязательно находится в пределах ширины ямы 0 ¸ а, следовательно, вероятность этого события равна 1.
|
Выразим плотность вероятности 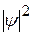 , используя пси-функцию (·), подставим w, и найдем интеграл. Учтем, что из тригонометрии: 2 sin2a = 1- cos2a.
, используя пси-функцию (·), подставим w, и найдем интеграл. Учтем, что из тригонометрии: 2 sin2a = 1- cos2a.
Учитывая, что интеграл равен 1, получим выражение для А:
Зная А и w, найдем окончательный вид решения:
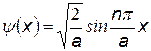
| Пси-функция для частицы в одномерной прямоугольной яме, физического смысла не имеет.
|
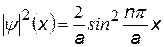
| Плотность вероятности для частицы в одномерной яме - определяет вероятность нахождения частицы на единичном отрезке ямы
|
Теперь осталось найти выражение для энергии электрона. Для этого нужно найти вторую производную пси-функции и подставить в уравнение [. Получим:
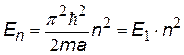
| энергия частицы в одномерной потенциальной яме,
|
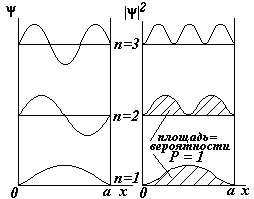
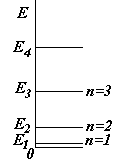 На рис. показаны энергетические уровни частицы, пси-функция и плотность вероятности для первых трех квантовых состояний. Площади под кривыми плотности вероятности
На рис. показаны энергетические уровни частицы, пси-функция и плотность вероятности для первых трех квантовых состояний. Площади под кривыми плотности вероятности 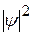 представляют собой вероятности, т.к.
представляют собой вероятности, т.к.  .
.
Что можно сказать о поведении частицы? В зависимости от того, какова ее энергия, вероятность обнаружить частицу различная. Например, при наименьшей энергии Е1 частица пребывает в основном в середине ямы, а при энергии Е2 вероятность обнаружить частицу в середине ямы равна нулю.

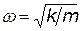 . Посмотрим, к каким результатам приведет решение уравнения Шрёдингера (a), если его применить к одномерной частице, которая обладает такой потенциальной энергией.
. Посмотрим, к каким результатам приведет решение уравнения Шрёдингера (a), если его применить к одномерной частице, которая обладает такой потенциальной энергией.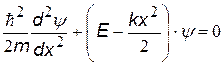

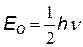 при
n = 0
при
n = 0
 По классическим представлениям при Т ® 0 К энергия должна стремиться к 0, решение уравнения Шрёдингера приводит к выводу о существовании нулевой энергии;
По классическим представлениям при Т ® 0 К энергия должна стремиться к 0, решение уравнения Шрёдингера приводит к выводу о существовании нулевой энергии;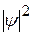 при различных энергиях Е осциллятора. Если мы спросим себя, а как ведет себя частица, ведь нам всегда хочется наглядно представить процессы. Ответ – не знаем, ведь квантовый объект имеет двойственную природу. Мы можем только сказать, что частица находится в потенциальной яме, имеет определенный набор энергий и, если ее энергия равна, например Е1, то вероятность обнаружить ее в середине ямы равна нулю. При переходе на другой уровень энергия частицы меняется дискретно, и система поглощает или испускает порцию энергии hn.
при различных энергиях Е осциллятора. Если мы спросим себя, а как ведет себя частица, ведь нам всегда хочется наглядно представить процессы. Ответ – не знаем, ведь квантовый объект имеет двойственную природу. Мы можем только сказать, что частица находится в потенциальной яме, имеет определенный набор энергий и, если ее энергия равна, например Е1, то вероятность обнаружить ее в середине ямы равна нулю. При переходе на другой уровень энергия частицы меняется дискретно, и система поглощает или испускает порцию энергии hn.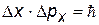
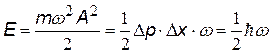
 .
. 1).Частица находится в прямоугольной потенциальной яме, внутри ямы потенциальная энергия U постоянна, примем ее равной нулю = 0. Высота стенок ямы ® ¥, т.е. частица не может выйти из ямы (см.рис.).
1).Частица находится в прямоугольной потенциальной яме, внутри ямы потенциальная энергия U постоянна, примем ее равной нулю = 0. Высота стенок ямы ® ¥, т.е. частица не может выйти из ямы (см.рис.). [
[
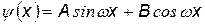 . Для нахождения коэффициентов А и В используем краевое условие
. Для нахождения коэффициентов А и В используем краевое условие 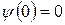 , смысл которого в том, что частица не может выйти из ямы.
, смысл которого в том, что частица не может выйти из ямы.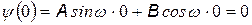
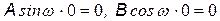 , т.к. sin 0 = 0, а cos 0 = 1 ¹ 0, то В = 0
, т.к. sin 0 = 0, а cos 0 = 1 ¹ 0, то В = 0
 ·
·
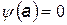





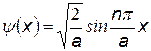
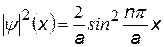
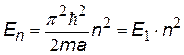

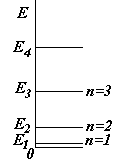 На рис. показаны энергетические уровни частицы, пси-функция и плотность вероятности для первых трех квантовых состояний. Площади под кривыми плотности вероятности
На рис. показаны энергетические уровни частицы, пси-функция и плотность вероятности для первых трех квантовых состояний. Площади под кривыми плотности вероятности  .
.


