| 1) n = 1, 2, 3, …, ¥
главное квантовое число
| входит в выражение для энергии электрона [xvi] Для основного состояния атома Н (n = 1) – см. ранее.
|
| 2) l = 0, 1, 2, …, (n - 1) - орбитальное квантовое число,
Входит в выражения для орбитальных механического Lорб и магнитного pорб моментов электрона в атоме. Показывает, что орбитальные моменты квантуются, т.е. могут принимать только дискретные значения.
|
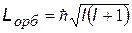 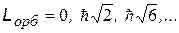
| 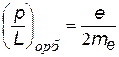
 Отношение орбитальных магнитного и механического моментов
Как векторы они направлены противоположно Отношение орбитальных магнитного и механического моментов
Как векторы они направлены противоположно
|
| механический орбитальный момент (момент импульса)
|
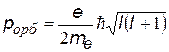 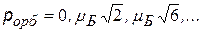
|
| магнитный орбитальный момент
m e – масса электрона
|
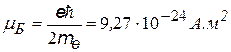
| магнетон Бора; (магнитные моменты принято
выражать в магнетонах Бора)
|
3) m = - l, …, -1, 0, +1, …, +l - магнитное квантовое число
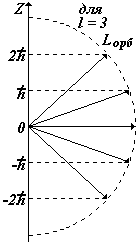
Входит в выражение для проекций орбитальных моментов на направление Z внешнего поля (например, магнитного).
Показывает, что плоскость, в которой движется электрон во внешнем поле ориентируется только определенным образом, так чтобы проекция момента была кратна  – см.рис. – см.рис.
| 
|
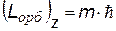
| 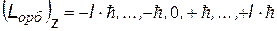
|
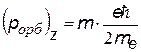
| 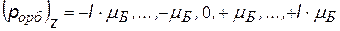
|
4) 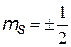 ms - магнитное собственное квантовое число;
Входит в выражение для проекций собственного механического Lсобст и магнитного рсобст моментов на направление Z внешнего поля (например, магнитного). Показывает, что ориентация Lсобст (спина –см. дальше) может иметь только два значения. ms - магнитное собственное квантовое число;
Входит в выражение для проекций собственного механического Lсобст и магнитного рсобст моментов на направление Z внешнего поля (например, магнитного). Показывает, что ориентация Lсобст (спина –см. дальше) может иметь только два значения.
|
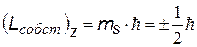
| 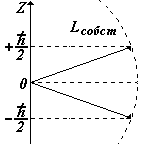
| 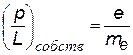
|

| отношение собственных магнитного и механического моментов
|
Спин (от англ. spin - веретено). Спином называется собственный механический момент (момент импульса) электрона  , связанный с некоторым движением («вращением») электрона вокруг собственной оси (см.рис.) , связанный с некоторым движением («вращением») электрона вокруг собственной оси (см.рис.)
| 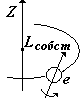
|
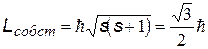
| Спин - собственный механический момент (момент импульса) электрона –имеет только одно значение.Спин связан со спиновым квантовым числом s, имеющим также только одно значение ½.
|
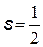
| спиновое квантовое
число
|
В квантовой механике различают частицы с «целым» спином (бозоны) и «полуцелым» спином (фермионы, например, электрон, см. дальше).Это условная терминология. Из формулы для спина видно, что он не может быть целым числом. В этих словах подразумевается, что проекция спина либо кратна  , либо кратна половине , либо кратна половине  . .
|
| | | | |
Таким образом, из квантовой механики следует, что энергия электрона, его орбитальные моменты, проекции орбитальных моментов на внешнее поле - квантуются. Они не могут иметь любые значения, а только те, которые определяются приведенными выше соотношениями. Собственный момент электрона имеет только одно значение, а его проекция на внешнее поле – два значения ±  / 2. Часто условно говорят «спин вверх», «спин вниз».
/ 2. Часто условно говорят «спин вверх», «спин вниз».
 Чтобы представить сложность поведения электрона даже в простейшем атоме Н, на рисунке представлена плотность вероятности для электрона в состоянии с n = 4, l = 2, m = ± 1. Светлые пятна - это области, в которых наиболее вероятно пребывание электрона. Это только плоский срез, в действительности вероятность имеет объемное распределение.
Чтобы представить сложность поведения электрона даже в простейшем атоме Н, на рисунке представлена плотность вероятности для электрона в состоянии с n = 4, l = 2, m = ± 1. Светлые пятна - это области, в которых наиболее вероятно пребывание электрона. Это только плоский срез, в действительности вероятность имеет объемное распределение.

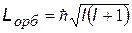
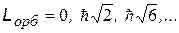
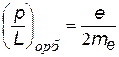
 Отношение орбитальных магнитного и механического моментов
Как векторы они направлены противоположно
Отношение орбитальных магнитного и механического моментов
Как векторы они направлены противоположно
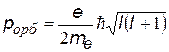
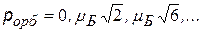
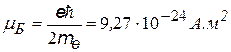
 – см.рис.
– см.рис.

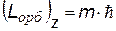
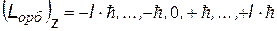
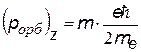
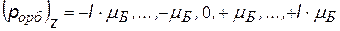
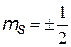 ms - магнитное собственное квантовое число;
Входит в выражение для проекций собственного механического Lсобст и магнитного рсобст моментов на направление Z внешнего поля (например, магнитного). Показывает, что ориентация Lсобст (спина –см. дальше) может иметь только два значения.
ms - магнитное собственное квантовое число;
Входит в выражение для проекций собственного механического Lсобст и магнитного рсобст моментов на направление Z внешнего поля (например, магнитного). Показывает, что ориентация Lсобст (спина –см. дальше) может иметь только два значения.
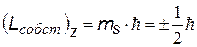
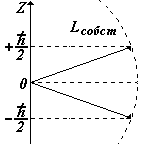
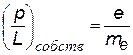

 , связанный с некоторым движением («вращением») электрона вокруг собственной оси (см.рис.)
, связанный с некоторым движением («вращением») электрона вокруг собственной оси (см.рис.)
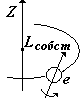
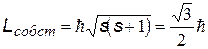
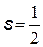
 Чтобы представить сложность поведения электрона даже в простейшем атоме Н, на рисунке представлена плотность вероятности для электрона в состоянии с n = 4, l = 2, m = ± 1. Светлые пятна - это области, в которых наиболее вероятно пребывание электрона. Это только плоский срез, в действительности вероятность имеет объемное распределение.
Чтобы представить сложность поведения электрона даже в простейшем атоме Н, на рисунке представлена плотность вероятности для электрона в состоянии с n = 4, l = 2, m = ± 1. Светлые пятна - это области, в которых наиболее вероятно пребывание электрона. Это только плоский срез, в действительности вероятность имеет объемное распределение.


