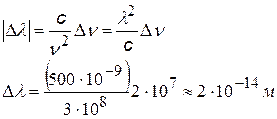В классической механике предполагалось, что координата точки и ее импульс могут быть определены одновременно с любой точностью. Попробуем понять, какие трудности возникают, если пытаться применить классические понятия к объекту, обладающему двойственной природой (частица-волна). Рассмотрим так
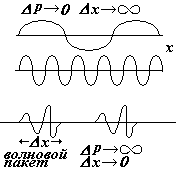 называемый пакет волн. Если сложить несколько волн с различными частотами, распространяющиеся в направлении х, получится сложная несинусоидальная волна [xi]. Если будет складываться очень большое число волн со всевозможными длинами, образуется волновой пакет шириной D х (см.рис.). Монохроматическая волна имеет определенную длину волны и, соответственно импульс р = h / l = const,
называемый пакет волн. Если сложить несколько волн с различными частотами, распространяющиеся в направлении х, получится сложная несинусоидальная волна [xi]. Если будет складываться очень большое число волн со всевозможными длинами, образуется волновой пакет шириной D х (см.рис.). Монохроматическая волна имеет определенную длину волны и, соответственно импульс р = h / l = const,
D р ® 0, а протяженность ее D х ® ¥. Очень узкий волновой пакет содержит множество волн, количество которых в пределе стремится к бесконечности и разброс импульсов в нем D р ® ¥ [xii], а протяженность
D х ® 0. Т.о., мы приходим к выводу, чем более точно локализован волновой пакет, тем больше оказывается неопределенность в его импульсе.
Гейзенберг выдвинул принцип неопределенности: «Существует принципиальное ограничение на точность, с которой могут быть определены физические величины, не связанное с точностью приборов». Он предложил также формулы, смысл которых в следующем.
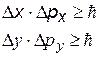
| соотношения неопределенностей для координаты и импульса [xiii] «Если измеряется координата х частицы и одновременно проекция ее импульса в направлении х - (рх), то минимальные
ошибки при их одновременном измерении связаны этими соотношениями»
|
Существует также соотношение неопределенности, касающееся энергии и времени.
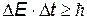
| соотношения неопределенностей для энергии и времени.
«Если атомная система обладает энергией Е в течение времени t, то одновременное измерение этих величин возможно лишь с точностью, определяемой данным соотношением»
|
Из соотношений неопределенностей следует, что чем точнее определяется одна величина, тем менее точно – другая при одновременном их измерении,. Так как 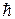 очень мало, то эти ограничения существенны только в атомных масштабах.
очень мало, то эти ограничения существенны только в атомных масштабах.
С помощью соотношений неопределенностей можно дать простые объяснения фактам, установленным другими путями. Например.
1). Входит ли электрон в состав атомного ядра?
| D х = 10-14 м
| Размер ядра по порядку величины
|
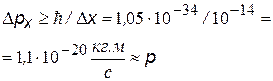
| Предположим, что электрон находится в ядре. Найдем неопределенность в его импульсе и примем ее равной самому импульсу[xiv]
|
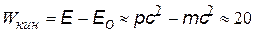 МэВ МэВ
| кинетическая энергия релятивистского электрона в ядре (считаем, что он движется как квант со скоростью с)
|
| Из опытов по радиоактивному бета-распаду известно, что энергии вылетающих из ядра электронов значительно меньше. Следовательно, в ядре «готовых» электронов нет; электрон образуется в ядре при превращении нейтрона в протон.
|
2). Оценим с помощью соотношения неопределенностей энергию связи электрона в атоме водорода.
| D х =0,5 10-10 м
| размер атома Н
|
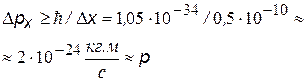
| импульс электрона, вычисленный с помощью соотношения неопределенности
|
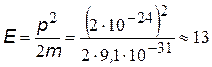 эВ эВ
| Энергия нерелятивистского электрона
(1 эВ=1,6×10-19 Дж). По порядку величины совпадает с энергией, вычисленной по теории Бора
|
3). Найдем предел точности, с которой можно определить частоту и длину волны излучаемого света
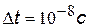
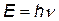
| время возбужденного атома, спустя это время электрон возвращается на нижележащую орбиту, и атом испускает квант света с энергией Е
|
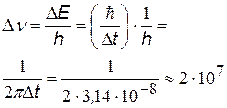 Гц Гц
| предел точности определения частоты излучения, найденный с помощью соотношения неопределенности
|
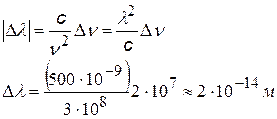
| предел точности измерения длины световой волны для зеленого света
l =(500,0000000 ± 0,0000002) нм
с = 3×108 м/с – скорость света в вакууме
|

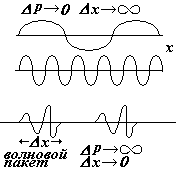 называемый пакет волн. Если сложить несколько волн с различными частотами, распространяющиеся в направлении х, получится сложная несинусоидальная волна [xi]. Если будет складываться очень большое число волн со всевозможными длинами, образуется волновой пакет шириной D х (см.рис.). Монохроматическая волна имеет определенную длину волны и, соответственно импульс р = h / l = const,
называемый пакет волн. Если сложить несколько волн с различными частотами, распространяющиеся в направлении х, получится сложная несинусоидальная волна [xi]. Если будет складываться очень большое число волн со всевозможными длинами, образуется волновой пакет шириной D х (см.рис.). Монохроматическая волна имеет определенную длину волны и, соответственно импульс р = h / l = const,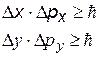
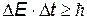
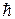 очень мало, то эти ограничения существенны только в атомных масштабах.
очень мало, то эти ограничения существенны только в атомных масштабах.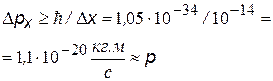
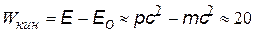 МэВ
МэВ
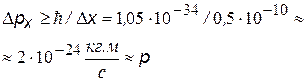
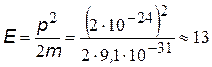 эВ
эВ
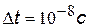
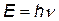
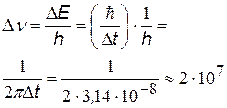 Гц
Гц