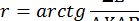ОРИЕНТИРОВАНИЕ ЛИНИЙ. РЕШЕНИЕ ПРЯМОЙ И ОБРАТНОЙ ГЕОДЕЗИЧЕСКИХ ЗАДАЧ.
Ориентировать линию – это определить ее положение относительно направления, принятого за исходное. В геодезии за исходное направление принимают истинный, магнитный или осевой меридианы. В зависимости от вида исходного меридиана различают истинный и магнитный азимуты, дирекционный угол и румбы. Азимутом называется горизонтальный угол, отсчитываемый от северного направления меридиана по ходу часовой стрелки до направления данной линии. Азимут называется истинным А, если отсчитывается от истинного меридиана, и магнитным Ам, если от магнитного. Дирекционным углом α; называется горизонтальный угол, отсчитываемый от северного направления осевого меридиана по ходу часовой стрелки до направления данной линии. Азимуты и дирекционный угол измеряются от 0° до 360°. Румбом r линии называется горизонтальный угол, отсчитываемый от ближайшего направления меридиана до направления данной линии. Румбы измеряются от 0° до 90°. Зависимость между значением румбов и дирекционных углов приведена в табл. 3.1.
Таблица 3.1
В геодезии приняты следующие обозначения меридианов:
Истинные меридианы разных точек линии не параллельны между собой, поэтому истинные азимуты точек линий также не одинаковы (рис. 3.1).
Следовательно, прямая линия местности при построение ее на плане по истинному азимуту изобразится ломаной. Напротив, дирекционный угол одинаков в любой точке линии. Поэтому все геодезические сети ориентируют по дирекционным углам. Угол между направлениями истинного и осевого меридианов называется сближением меридианов γ;. Сближение меридианов считают положительным, если осевой меридиан расположен к востоку от истинного, и отрицательным - к западу (рис. 3.2).
Рис. 3.2. Сближение и склонение меридианов Обычно на картах измеряют дирекционный угол, а истинный азимут вычисляют по формуле А = α + (±γ). В некоторых случаях геодезические построения ориентируют по магнитному меридиану. Магнитные меридианы сходятся в магнитном полюсе Земли, который не совпадает с географическим полюсом. Угол между направлениями истинного и магнитного меридианов называется склонением магнитной стрелки δ; (рис. 3.3). Склонение считается положительным, если магнитный меридиан расположен к востоку от истинного, и отрицательным – к западу. По значению истинного азимута можно вычислить магнитный Ам = А – (±δ). При ориентировании линии часто используют обратные углы. На рис. 3.3 азимут направления ВС называется прямым, а СВ — обратным. Прямой и обратный истинный азимуты различаются на величину сближения меридианов АВС = АСВ ± 180° ± γ;.
Рис. 3.3. Прямой и обратный азимуты Прямой и обратный дирекционные углы различаются на 180° αОБ = αПР ± 180°. Прямой румб отличается от обратного только названием.
Например: румб линии ВС равен rВС = СВ: 68°, а линии СВ – rСВ = ЮЗ: 68°.
При вычислении в геодезии дирекционных углов линий используют зависимость между дирекционными и горизонтальными углами сторон хода (рис.3.4). Сущность решения заключается в следующем. По известному дирекционному стороны АВ и горизонтальным углам βП и βЛ вычисляют дирекционный стороны ВС.
Рис. 3.4. Зависимость между углами хода и дирекционными углами сторон хода При измеренных правых углах дирекционный последующей стороны вычисляют по формуле αВС=αАВ – βП + 180°, и при левых αВС=αАВ + βЛ - 180°.
Дирекционные углы на картах измеряют и строят геодезическим транспортиром - А с ценой деления 30', с оценкой деления транспортира на глаз и округлением до 5'. При измерении угла центральную метку (ноль прямолинейной шкалы) совмещают с вершиной угла, а нулевой диаметр (0° и 180°) должен находится на линии (осевом меридиане). При этом возможны следующие случаи: - если угол меньше 180°, то измерение ведут от осевого меридиана до направления сторон; - если угол больше 180°, тогда измеряют угол между продолжением сторон треугольника или его дополнением до 180°; - при сторонах измеряемого угла меньше радиуса транспортира, их следует удлинить выверенной линейкой.
Геодезическая прямая задача – по координатам одной точки, дирекционному углу и горизонтальному проложению находятся координаты второй точки.
Знаки приращений координат зависят от величины значения дирек- ционного угла.
Даны координаты ХА, YА точки А, дирекционный угол αАВ и расстояние dАВ между этими точками. Требуется найти координаты ХВ, YВ точки В. Из рис.23 следует, что координаты точки В равны: ХВ = ХА + ΔХАВ; YВ = YА + ΔYАВ, где ΔХАВ = ХВ – ХА; ΔYАВ = YВ – YА. Разности ΔХАВ и ΔУАВ называются приращением координат и вычисляются по формулам ΔХАВ = dАВ·cos αАВ, ΔYАВ = dАВ·sin αАВ. Знаки приращений координат зависят от величины значения дирекционного угла.
Пример: Длина линии d равна 1,095 км, угол α; равен 85°33,0', а координаты точки А равны ХА = 6065,251 км и YA = 4311,975 км. Найдем: ХВ =6065,251 +1,095cos85°33' = 6065,251 + (-0,085) = 6065,166; Y В = 4311,975 +1,095sin 85°33' = 4311,975 + 1,092 = 4313,067.
Геодезическая обратная задача - по известным координатам двух точек требуется найти дирекционный угол и горизонтальное проложение линии. Даны прямоугольные координаты двух точек А (хА, уА) и В (хВ, уВ). Из рисунка 23 следует, что румб линии АВ равен:
Г = ^S-r^, (15) где АХав, АУАВ - приращение координат. Для вычисления дирекционного угла аАВ, по знакам приращения координат определяют название четверти (румба). Зная румб, используя таблицу 2, вычисляют дирекционный угол.
сгзядв зинход Правильность определения дирекционного угла проверяется по чертежу или решением прямой задачи.
Пример: координаты точек А и В равны ХА = 6065,251 км; ХВ = 6065,166 км, УА = 4311,975 км; YB = 4313,067 км. Вычислим приращение координат: Δ;Хав= ХВ - ХА = - 0,085; ΔY AВ = Yb - YA = 1,092.
Определим величину румба
По знакам приращений координат – ΔХАВ и + ΔУАВ из таблицы 2 видно, что направление АВ находится во второй четверти, и дирекционный угол равен α = 94°27,0’. Находим длину линии d = 1,095 км.
Задание 1. Вычислить координаты точки В линии АВ. Исходные координаты точки А, длину линии dAB и дирекционный угол аАВ взять из таблиц приложения Б. Вычисленные значения координат точки В сравнить с определенными по карте. Результаты вычислений поместить в соответствующей графе приложения Б.
Задание 2 Определить дирекционный угол и длину линии АВ треугольника АВС (данного на карте). Вычисления выполнить в таблице, полученные данные сравнить с определенными на карте. Данные занести в приложение Б. Решение обратной задачи
Задание: 1. Измерить транспортиром дирекционные углы линий АВ, ВС и СА. 2. Вычислить румбы линий. 3. Вычислить обратные дирекционные углы линий. 4. Вычислить истинные и магнитные азимуты линий. Значения сближения и склонения меридианов даны на схеме под южной рамкой карты.
5. Полученные результаты занести в таблицу приложения Б.
|

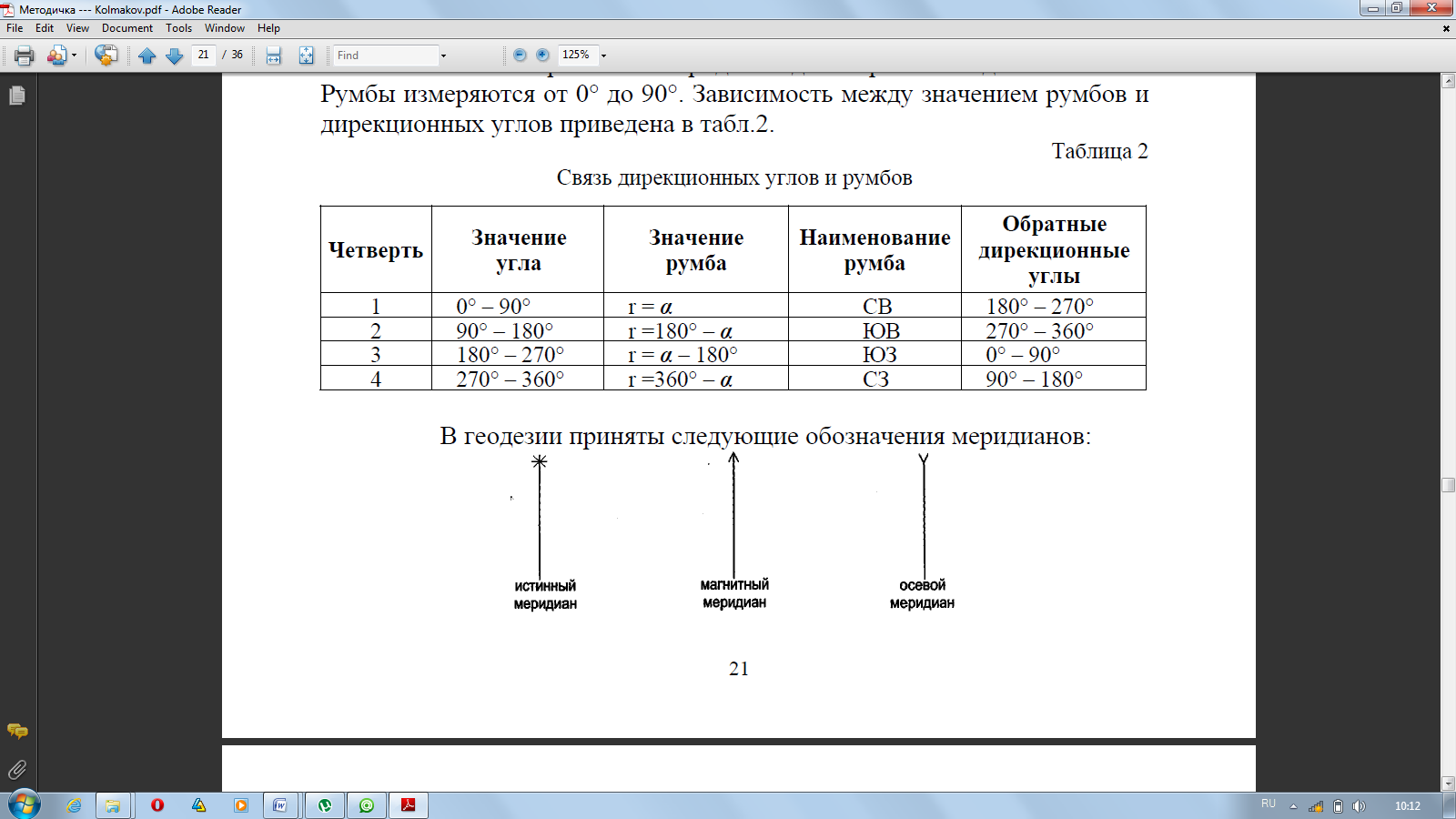
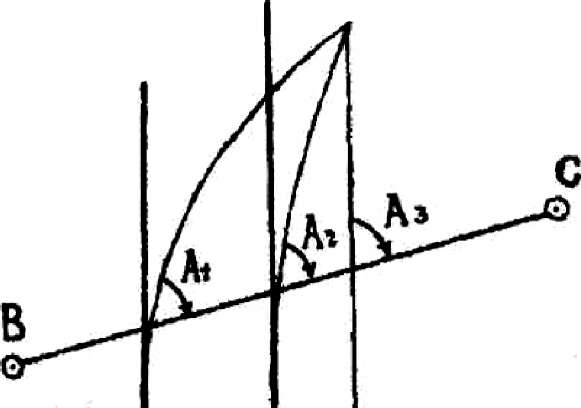 Рис. 3.1. Истинные азимуты линий
Рис. 3.1. Истинные азимуты линий
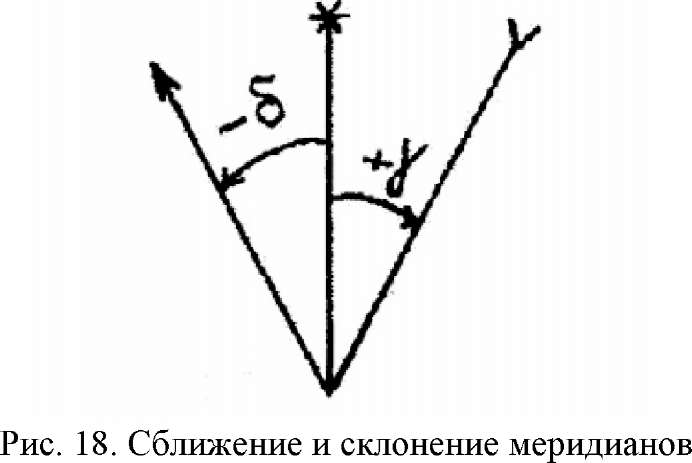
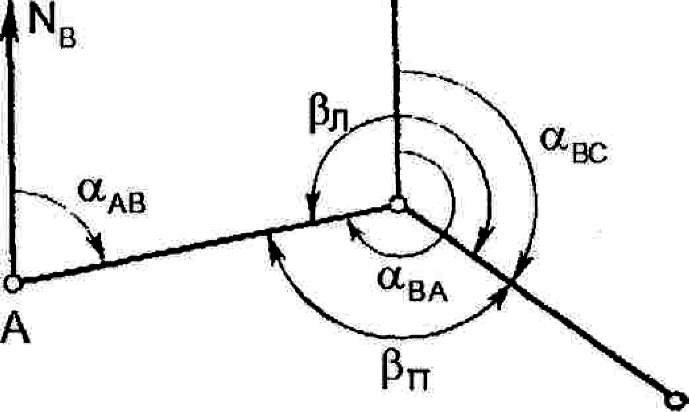
 Рис. 3.5. Прямая и обратная геодезические задачи
Рис. 3.5. Прямая и обратная геодезические задачи