Модель функционирования З П С, оснащённой «n» однородными факторами воздействия на поставки товаров и услуг из другого региона
Вывод основных ДУ
Полагаем, что время обслуживания З П С величина случайная и подчинена показательному закону распределения с параметром ν. Поэтому вероятность того, что время обслуживания поставки не превосходит t определяется выражением Р(t) = 1 - е Вероятность противоположного события равна g(t) = е А А А Составим дифференциальные уравнения этих состояний ЗПС. Обозначим через Δt очень маленький промежуток времени. Составим ДУ для состояния А - в момент времени t все факторы З П С себя не проявляют. За время Δt в области действия З П С не проявилась не одна поставка. Вероятность этого события равна Р - в момент времени t один из факторов себя уже проявляет. За время Δt в области действия З П С не проявилась ни одна поставка, а действующий фактор прекратил своё действие. Вероятность этого события равна Р Где Р Так как рассмотренные события несовместны, то составим уравнение состояния А Р Где Р не будет воздействовать на поставки; Р е одной поставки; (1 - е один из факторов прекратит свое воздействие на поставки. Величину е е а 1 - е Учитывая малость величины Δt. Можно уравнение (3) представить в виде, пренебрегая величинами более высокого порядка малости, ′ Р Преобразуем и разделим обе части уравнения (4) на Δt получим следующее соотношение Р Так как в соотношении Р Р Разделим обе части уравнения (6) на Δt получим следующее соотношение
и, перейдя к пределу Δt → 0, получим
Составим ДУ для состояния А - в момент времени t «k» факторов З П С занято обслуживанием поставок. За время Δt в область действия З П С не проявилась ни одна поставка и ни один из занятых факторов не освободился. Вероятность этого события равна Р - в момент времени t З П С находилась в состоянии А Р - в момент времени t З П С находилась в состоянии А Р Тогда Р После аналогичных преобразований получаем
Это уравнение справедливо для случая 0≤ k≤ n. Рассмотрим состояние А - в момент времени t З П С находилась в состоянии А Р После соответствующих преобразований и перехода к пределу при Δt → 0, получим
В итоге мы получили систему дифференциальных уравнений, которая описывает вероятности переходов состояний З П С, оснащённой n однородными факторами воздействия на поставки товаров и услуг из другого региона.
…………………………………….
………………………………………
Совокупность этих уравнений получила название системы уравнений Эрланга.
|


 может находиться в следующих состояниях:
может находиться в следующих состояниях: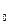 - все факторы ЗПС не проявляют себя.
- все факторы ЗПС не проявляют себя. - k – факторов себя проявляют себя, а остальные свободны от облуживания.
- k – факторов себя проявляют себя, а остальные свободны от облуживания. - все факторы ЗПС проявили себя и обслуживают поставки.
- все факторы ЗПС проявили себя и обслуживают поставки.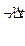 (1)
(1) (t) (1 - е
(t) (1 - е  ) е
) е 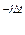 (2)
(2)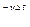 )е
)е 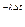 е
е 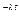 (3)
(3) ) - вероятность того, что за время Δt в области действия З П С
) - вероятность того, что за время Δt в области действия З П С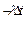 ≈ 1 - λ Δt + …,
≈ 1 - λ Δt + …, ≈ νΔt + …,
≈ νΔt + …, , то можно допустить, что Δt
, то можно допустить, что Δt 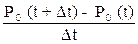 = - Р
= - Р  (
( Р
Р  (t) = - Р
(t) = - Р  . За время Δt в области действия З П С проявилась одна поставка, но ни один из действующий факторов не прекратил обслуживание своей поставки. Вероятность этого события равна
. За время Δt в области действия З П С проявилась одна поставка, но ни один из действующий факторов не прекратил обслуживание своей поставки. Вероятность этого события равна . За время Δt в освободился один факторов З П С и в области действия З П С не проявилась ни одна поставка. Вероятность этого события равна
. За время Δt в освободился один факторов З П С и в области действия З П С не проявилась ни одна поставка. Вероятность этого события равна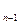 (t). (14)
(t). (14)


