Транспортная задача. Постановка задачи . Есть однотипная продукция, которая находится на складах А1, А2, А3 и А4
Постановка задачи. Есть однотипная продукция, которая находится на складах А1, А2, А3 и А4. Запасы на каждом складе составляют а1=200, а2=350, а3=300 и а4=150. Это можно записать виде матрицы:
Составить план перевозок таким образом, чтобы: 1) все товары были вывезены; 2) все потребители были удовлетворены; 3) общая стоимость перевозок была бы минимальной.
Решение. Проверим, выполняется ли балансовое условие, т.е. равен ли спрос и предложение. 1) предложение составляет: 2) спрос равен: т.к.
Метод минимальной стоимости. Выбираем клетки с минимальной стоимостью, сравниваем потребности Таблица перевозок
1. Наименьшая стоимость =1. На складе есть 150, а нужно 410. Поэтому поставляем 150, и тогда на складе А4 ничего не осталось, его вычеркиваем. 2. следующая цена =2. Сравниваем: у А1 есть 200, но В1 нужно 170. берем 170 и потребителя В1 вычеркиваем, т.е. ему уже ничего не нужно. Аналогично сравниваем В3 (ему еще нужно 260) и склад А2 (там есть 350). Берем 260 и вычеркиваем потребителя В3, т. к. он все уже получил. 3. следующая стоимость =3. У А1 еще осталось 200-170=30, которые отдаем В4, и А1 вычеркиваем. Аналогично для В2 мы можем взять 90, которые остались у А2. Т.к. у А2 уже ничего нет, то его вычеркиваем. 4. Клетки с ценами =4 и =5 уже вычеркнуты. Следующая стоимость =6. В2 нужно еще 150, которые есть у А3 – берем их. 5. Осталась клетка со стоимостью =7. Нужно 150 и есть 150, т.к. задача закрытая. План составлен. Проверяем его на оптимальность по методу потенциалов. Исходному плану отвечала стоимость перевозок:
Таблица потенциалов (начало)
В те клетки, куда были сделаны поставки, проставляем стоимость перевозки. Это сумма потенциалов по заполненным клеткам. Пусть U1= 0, тогда U1+ V1=2, следовательно, V1= 2. Так как U1=0, а U1+ V4=3, то V4= 3. Так как U3+ V4=7, то U3= 4 Так как U3+ V2=6, то V2= 2. Так как U2+ V2=3, то U2= 1. Так как U2+ V3=2, то V3= 1. Так как U4+ V3=1, то U4= 0. Потенциалы расставлены, теперь проверяем оценки для свободных клеток:
Сумму потенциалов записываем в левом нижнем углы ячейки, а стоимость – в правом верхнем.
Таблица потенциалов (окончание)
Т.к. есть положительная оценка, то план не оптимальный: Делаем поставку в клетку с положительной оценкой. Контур перераспределения начинаем с той клетки, куда делаем поставку, и затем поворачиваем под прямым углом только в заполненных клетках (контур показан пунктиром). Ставим по очереди знаки «+» и «-». Отрицательным углам отвечают поставки 170 и 150. Выбираем меньшее: Выигрыш функции цели: Такой груз мы перераспределяем по контуру: прибавляем в положительных углах и отнимаем в отрицательных. Там, где углов контура нет. Поставки остаются без изменений. Получаем новый план перевозок:
Стоимость перевозок по этому плану:
Ему соответствует таблица потенциалов:
Положительных оценок нет, значит, план оптимальный. Запишем в виде матрицы:
Этому плану отвечала стоимость перевозок:
Т.к. для свободной клетки есть нулевая оценка, то возможен еще один оптимальный план с той же стоимостью перевозки. Для того, чтобы его найти, перераспределим по контуру
|

 . Есть потребители этой продукции В1, В2, В3 и В4. Их потребности составляют в1=170; в2=240; в3=410 и в4=180. Это можно записать виде матрицы:
. Есть потребители этой продукции В1, В2, В3 и В4. Их потребности составляют в1=170; в2=240; в3=410 и в4=180. Это можно записать виде матрицы:  . Известна матрица стоимости перевозки единицы груза от каждого поставщика каждому потребителю:
. Известна матрица стоимости перевозки единицы груза от каждого поставщика каждому потребителю: .
. 200+350+300+150=1 000;
200+350+300+150=1 000; 170+240+410+180=1 000;
170+240+410+180=1 000; , то задача закрытая, и можно составлять план перевозок.
, то задача закрытая, и можно составлять план перевозок.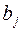 и возможности
и возможности  по данной клетке и делаем в нее поставку в размере:
по данной клетке и делаем в нее поставку в размере: 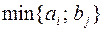 и так далее до тех пор, пока мы заполним всю таблицу.
и так далее до тех пор, пока мы заполним всю таблицу. 170
170

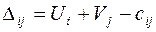 .
. .
.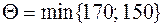 =150.
=150.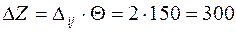
 90
90

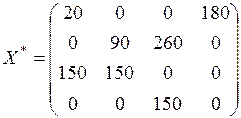
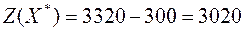 .
. . Получим:
. Получим:


