Метод потенциалов. Метод потенциалов позволяет, исходя из некоторого первоначального опорного плана, построить оптимальный план перевозок транспортной задачи
Метод потенциалов позволяет, исходя из некоторого первоначального опорного плана, построить оптимальный план перевозок транспортной задачи. Метод потенциалов основан на использовании следующей теоремы. Теорема. Если план Х*=(xij*) транспортной задачи является оптимальным, то ему соответствует система из (m+n) чисел Ui* и Vj*, удовлетворяющих условиям: Ui*+Vj*=cij для xij*>0 и Ui*+Vj*≤cij для xij=0. Числа Ui* и Vj* называется соответственно потенциалами поставщиков и потребителей.
Построение системы потенциалов. По числу поставщиков и потребителей вводятся соответственно потенциалы Ui+Vj=cij, (1) где cij – стоимость перевозки единицы груза занятой клетки в i-той строке и j-м столбце. Задавая значение одного потенциала произвольно (обычно U1=0), остальные определяют из уравнений (1).
Построение относительных оценок Для незанятых клеток вычисляем относительные оценки dij=cij-(Ui+Vj) Определение оптимальности плана и перехода к новому плану. Если все dij≥0, то построенный план является оптимальным. Если существует отрицательная оценка, то план не является оптимальным и его можно улучшить. Среди отрицательных оценок выбираем наименьшую (т.е. наибольшую по модулю). Это и будет клетка, соответствующая новой базисной переменной Обозначаем эту клетку знаком “+” и строим цикл: ломаную линию, вершины которой находятся в клетке i0j0 и в клетках старого базиса (занятых). Циклом может служить самопересекающаяся ломаная, но точки её самопересечения не являются вершинами цикла. При построении цикла все повороты осуществляются под прямым углом. Такой цикл существует и является единственным. Поочередно проставляем в вершинах цикла “+” и “-“. Находим Q=min x’ij, где x’ij – перевозки стоящие в вершинах цикла, отмеченных знаком “-“. Двигаясь по циклу, вычитаем Q из объёмов перевозок в клетках, отмеченных знаком “-“, и прибавляем к объёмам перевозок в клетках, отмеченных знаком “+”. Новый опорный план подлежит проверке на оптимальность. Для этого нужно вновь построить систему потенциалов и проверить выполнение условий оптимальности для каждой незанятой клетки.
|

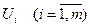 и
и  , связанные между собой соотношениями
, связанные между собой соотношениями .
.


