Транспортная задача.
Сущность транспортной задачи линейного программирования состоит в наивыгоднейшем прикреплении поставщиков однородного продукта ко многим потребителям этого продукта. Сформулируем транспортную задачу в общем виде. У m поставщиков A1, A2, …, Am сосредоточено соответственно a1, a2, …, am единиц некоторого одного груза, который необходимо доставить n потребителями B1, B2, …, Bn в количестве b1, b2, …, bn единиц соответственно. Известна стоимость cij перевозки груза от i-того поставщика к j-тому потребителю. Необходимо составить план перевозок, позволяющий вывезти все грузы, полностью удовлетворить потребителей и имеющий минимальную стоимость. Обозначим через xij количество единиц груза, запланированного к перевозке от i-того поставщика к j-тому потребителю. Тогда математическая модель транспортной задачи имеет следующий вид. Найти минимальное значение линейной функции:
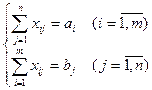
xij≥0
В рассмотренной модели предполагается, что суммарные запасы равны суммарным потребностям, т.е. Рассмотрим как открытую задачу формально преобразовать в закрытую. Если суммарный запас продукта превышает общий спрос, т.е.
то в рассмотрение вводится фиктивный (n+1)-й пункт потребления Bn+1 со спросом, равным небалансу, т.е.
и одинаковыми тарифами равными нулю. В этом случае условие разрешимости выполняется, а величина целевой функции остаётся прежней, поскольку цены на дополнительные перевозки равны нулю. При этом грузы, которые должны быть перевезены в пункт Bn+1, фактически останутся в пункте отправления. Если же общий спрос потребителей больше суммарного запаса продукта, то вводится фиктивный (m+1)-й пункт отправления Am+1 с запасом продукта
Тарифы на доставку продукта фиктивным поставщиком полагают равными нулю, что не отразится на целевой функции. При решении транспортной задачи все данные помещаются в таблицу.
Построение начального опорного плана (метод северо – западного угла)
1. min{a1, b1}=a1 (a1<b1) вычёркиваем всю 1-ую строку, кроме 1-ой клетки; вместо b1 пишем (b1-a1)
2. вычёркиваем весь 1-ый столбец, кроме 1-ой клетки, вместо a1 – (a1-b1)
3. min{a1, b1}=a1=b1 вычёркиваем либо строку, либо столбец. Если вычёркиваем строку, то во 2-ой строке под 1-ой клеткой пишут 0, а остальной столбец вычёркивают. Т.о., окажутся заполненными (m+n-1) клетка {расположены произвольно}. Они являются базисными. Для всех остальных клеток соответствующие xij=0 (их не пишем в клетках).
|

 {общая сумма затрат должна быть минимальной}
{общая сумма затрат должна быть минимальной}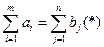 . Такая модель называется закрытой (или задачей с правильным балансом). В противном случае (если равенство (*) не выполняется) задача называется открытой.
. Такая модель называется закрытой (или задачей с правильным балансом). В противном случае (если равенство (*) не выполняется) задача называется открытой.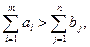
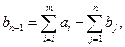


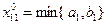
 min{a1, b1}=b1 (a1>b1)
min{a1, b1}=b1 (a1>b1)


