Вибір оптимального рішення за критерієм Байєса
| Варіант рішення
| Варіанти станів середовища
| V (Ai, Sj) · Pj
| max i { V (Ai, Sj) · Pj }
| | S 1
| S 2
| S 3
| | А 1
| 2,5
| 3,5
| 4,0
| 2,5 · 0,25 + 3,5 · 0,55 + 4,0 · 0,2 = 3,35
|
| | А 2
| 1,5
| 2,0
| 3,5
| 1,5 · 0,25 + 2,0 · 0,55 + 3,5 · 0,2 = 2,18
|
| | А 3
| 3,0
| 8,0
| 2,5
| 3,0 · 0,25 + 8,0 · 0,55 + 2,5 · 0,2 = 5,65
| А3
| | А 4
| 7,5
| 1,5
| 3,5
| 7,5 · 0,25 + 1,5 · 0,55 + 3,5 · 0,2 = 3,40
|
|
За критерієм Байєса оптимальним буде альтернативне рішення А 3.
Критерій Лапласа характеризується невідомим розподілом імовірностей на множині станів середовища та базується на принципі «недостатнього обґрунтування», який означає: коли немає даних для того, щоби вважати один зі станів середовища більш імовірним, то ймовірності станів середовища треба вважати рівними. Оптимальну альтернативу за критерієм Лапласа знаходимо за формулами:
для 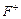 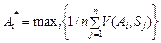 ; (3) ; (3)
для 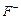 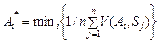 . (4) . (4)
Таблиця 3
Вибір оптимального рішення за критерієм Лапласа
| Варіант рішення
| Варіант стану середовища
| 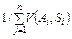
| max i {1/ nV (Ai, Sj)}
| | S 1
| S 2
| S 3
| | A1
| 2,5
| 3,5
| 4,0
| 1/3 · (2,5 + 3,5 + 4,0) = 3,33
|
| | A2
| 1,5
| 2,0
| 3,5
| 1/3 · (1,5 + 2,0 + 3,5) = 2,33
|
| | A3
| 3,0
| 8,0
| 2,5
| 1/3 · (3,0 + 8,0 + 2,5) = 4,50
| А3
| | A4
| 7,5
| 1,5
| 3,5
| 1/3 · (7,5 + 1,5 + 3,5) = 4,16
|
| За критерієм Лапласа оптимальним буде альтернативне рішення А 3 (табл. 3).
За правилом максимакс альтернативу знаходимо за формулою:
 . (5) . (5)
Скориставшись цим правилом, визначаємо максимальні значення для кожного рядка та вибираємо найбільше з них.
За правилом максимакс оптимальним буде альтернативне рішення А 3 (табл. 4).
Таблиця 4

Обзор компонентов Multisim Компоненты – это основа любой схемы, это все элементы, из которых она состоит. Multisim оперирует с двумя категориями...
|

Композиция из абстрактных геометрических фигур Данная композиция состоит из линий, штриховки, абстрактных геометрических форм...
|

Важнейшие способы обработки и анализа рядов динамики Не во всех случаях эмпирические данные рядов динамики позволяют определить тенденцию изменения явления во времени...
|

ТЕОРЕТИЧЕСКАЯ МЕХАНИКА Статика является частью теоретической механики, изучающей условия, при которых тело находится под действием заданной системы сил...
|
Условия, необходимые для появления жизни История жизни и история Земли неотделимы друг от друга, так как именно в процессах развития нашей планеты как космического тела закладывались определенные физические и химические условия, необходимые для появления и развития жизни...
Метод архитекторов Этот метод является наиболее часто используемым и может применяться в трех модификациях: способ с двумя точками схода, способ с одной точкой схода, способ вертикальной плоскости и опущенного плана...
Примеры задач для самостоятельного решения. 1.Спрос и предложение на обеды в студенческой столовой описываются уравнениями: QD = 2400 – 100P; QS = 1000 + 250P
1.Спрос и предложение на обеды в студенческой столовой описываются уравнениями: QD = 2400 – 100P; QS = 1000 + 250P...
|
Тема 2: Анатомо-топографическое строение полостей зубов верхней и нижней челюстей. Полость зуба — это сложная система разветвлений, имеющая разнообразную конфигурацию...
Виды и жанры театрализованных представлений
Проживание бронируется и оплачивается слушателями самостоятельно...
Что происходит при встрече с близнецовым пламенем
Если встреча с родственной душой может произойти достаточно спокойно – то встреча с близнецовым пламенем всегда подобна вспышке...
|
|

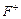
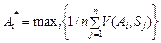 ; (3)
; (3)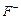
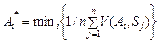 . (4)
. (4)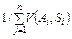
 . (5)
. (5)


