ВИБІР ОПТИМАЛЬНОГО РІШЕННЯ ЗА КРИТЕРІЄМ ВАЛЬДА
| Варіант рішення
| Варіанти станів середовища
| mіn j { V (Ai, Sj)}
| max i mіn j { V (Ai, Sj)}
| | S 1
| S 2
| S 3
| | А 1
| 2,5
| 3,5
| 4,0
| 2,5
| А 1
| | А 2
| 1,5
| 2,0
| 3,5
| 1,5
|
| | А 3
| 3,0
| 8,0
| 2,5
| 2,5
| А 3
| | А 4
| 7,5
| 1,5
| 3,5
| 1,5
|
| За критерієм Вальда оптимальними будуть альтернативні рішення А 1 і А 3, які вважаються еквівалентними, тобто мають однакові переваги для виконання.
Для того щоб застосувати критерій Севіджа, потрібно побудувати матрицю ризику як лінійне перетворення функціоналу оцінювання.
Для побудови матриці ризику використаємо такі формули:
для 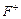 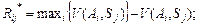 (8) (8)
для 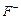 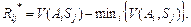 (9) (9)
Матрицю ризику побудуємо в табл. 6.
Таблиця 6
Побудова матриці ризику
| Варіант рішення
| Матриця прибутків (V (Ai, Sj))
| Матриця ризику (Rij)
| | Варіанти станів середовища
| Варіанти станів середовища
| | S 1
| S 2
| S 3
| S 1
| S 2
| S 3
| | А 1
| 2,5
| 3,5
| 4,0
| 7,5 – 2,5 = 5,0
| 8,0 – 3,5 = 4,5
| 4,0 – 4,0 = 0
| | А 2
| 1,5
| 2,0
| 3,5
| 7,5 – 1,5 = 6,0
| 8,0 – 2,0 = 6,0
| 4,0 – 3,5 = 0,5
| | А 3
| 3,0
| 8,0
| 2,5
| 7,5 – 3,0 = 4,5
| 8,0 – 8,0 = 0
| 4,0 – 2,5 = 1,5
| | А 4
| 7,5
| 1,5
| 3,5
| 7,5 – 7,5 = 0
| 8,0 – 1,5 = 6,5
| 4,0 – 3,5 = 0,5
| Тепер можна застосувати критерій Севіджа до матриці ризику за формулою:
 . (10) . (10)
Таблиця 7
Вибір оптимального рішення за критерієм Севіджа
| Варіант рішення
| Варіант стану середовища
| max j { Rij }
| min i max j { Rij }
| | S 1
| S 2
| S 3
| | А 1
| 5,0
| 4,5
|
| 5,0
|
| | А 2
| 6,0
| 6,0
| 0,5
| 6,0
|
| | А 3
| 4,5
|
| 1,5
| 4,5
| А 3
| | А 4
|
| 6,5
| 0,5
| 6,5
|
| За критерієм Севіджа оптимальним буде альтернативне рішення А 3 (табл. 7).
За допомогою критерію Гурвіца встановимо баланс між випадками крайнього оптимізму ат випадками крайнього песимізму за допомогою коефіцієнта оптимізму a. Цей коефіцієнт визначається від нуля до одиниці та показує ступінь схильностей особи, що приймає рішення, до оптимізму чи песимізму. Якщо a = 1, то це свідчить про крайній оптимізм, якщо a = 0 — крайній песимізм. За умов задачі a = 0,6.
Оптимальну альтернативу за критерієм Гурвіца знаходимо за формулами:
для 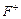 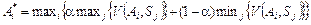 . (5.11) . (5.11)
для 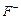  . (5.12) . (5.12)
Оптимальним рішенням за критерієм Гурвіца буде альтернативне рішення А 3 (табл. 8).
Таблиця 8
Вибір оптимального рішення за критерієм Гурвіца
| Варіант рішення
| Варіант стану середовища
| max j { V (Ai, Sj)}
| min j { V (Ai, Sj)}
| a · max j { V (Ai, Sj)} + + (1 – a)min j { V (Ai, Sj)}
| max i {a · max j { V ´´ (Ai, Sj)} + (1 – a) × × min j { V (Ai, Sj)}}
| | S 1
| S 2
| S 3
| | А 1
| 2,5
| 3,5
| 4,0
| 4,0
| 2,5
| 4,0 · 0,6 + 2,5 · 0,4 = 3,4
|
| | А 2
| 1,5
| 2,0
| 3,5
| 3,5
| 1,5
| 3,5 · 0,6 + 1,5 · 0,4 = 2,7
|
| | А 3
| 3,0
| 8,0
| 2,5
| 8,0
| 2,5
| 8,0 · 0,6 + 2,5 · 0,4 = 5,8
| А 3
| | А 4
| 7,5
| 1,5
| 3,5
| 7,5
| 1,5
| 7,5 · 0,6 + 1,5 · 0,4 = 5,1
|
|
Висновок: розрахунок за всіма даними критеріями довів доцільність виробництва продукції за альтернативним варіантом А 3.
5.3.2. Прийняття господарських рішень

Практические расчеты на срез и смятие При изучении темы обратите внимание на основные расчетные предпосылки и условности расчета...
|

Функция спроса населения на данный товар Функция спроса населения на данный товар: Qd=7-Р. Функция предложения: Qs= -5+2Р,где...
|

Аальтернативная стоимость. Кривая производственных возможностей В экономике Буридании есть 100 ед. труда с производительностью 4 м ткани или 2 кг мяса...
|

Вычисление основной дактилоскопической формулы Вычислением основной дактоформулы обычно занимается следователь. Для этого все десять пальцев разбиваются на пять пар...
|
Дезинфекция предметов ухода, инструментов однократного и многократного использования
Дезинфекция изделий медицинского назначения проводится с целью уничтожения патогенных и условно-патогенных микроорганизмов - вирусов (в т...
Машины и механизмы для нарезки овощей В зависимости от назначения овощерезательные машины подразделяются на две группы: машины для нарезки сырых и вареных овощей...
Классификация и основные элементы конструкций теплового оборудования Многообразие способов тепловой обработки продуктов предопределяет широкую номенклатуру тепловых аппаратов...
|
ОПРЕДЕЛЕНИЕ ЦЕНТРА ТЯЖЕСТИ ПЛОСКОЙ ФИГУРЫ Сила, с которой тело притягивается к Земле, называется силой тяжести...
СПИД: морально-этические проблемы Среди тысяч заболеваний совершенно особое, даже исключительное, место занимает ВИЧ-инфекция...
Понятие массовых мероприятий, их виды Под массовыми мероприятиями следует понимать совокупность действий или явлений социальной жизни с участием большого количества граждан...
|
|

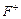
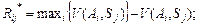 (8)
(8)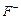
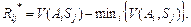 (9)
(9) . (10)
. (10)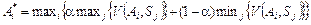 . (5.11)
. (5.11) . (5.12)
. (5.12)


