Вольтамперная характеристика идеализированного p-n-перехода.
Идеализированный p-n-переход – это упрощенная модель реального p-n- перехода, в котором пренебрегается процессами генерации и рекомбинации в обедненном слое и сопротивлением нейтральных областей, а также считается, что вне обедненного слоя электрическое поле отсутствует, и носители движутся только вследствие диффузии, носящей одномерный характер. Инжектированные носители диффундируют в глубь полупроводника и рекомбинируют с основными носителями. Через p-n- переход протекает ток, компенсирующий отвод носителей от границы: j=jдф+jдр Из уравнения диффузии для установившегося режима получаем:
Опуская индекс при p, это уравнение можно записать в виде
где Общее решение этого уравнения имеет вид
Коэффициенты A1 и A 2 находятся из граничных условий:
Отсюда A1= 0, A2= D p (0),
Градиент концентрации на границе перехода
Плотность дырочного тока равна
Аналогично, для плотности электронного тока получаем
где Dn и Ln – коэффициент диффузии электронов и диффузионная длина в p- области. Полный ток равен сумме токов электронов и дырок: I=S (jp+jn). Подставив (2.15), (2.16) в (2.19), (2.20), вольтамперную характеристику идеализированного p-n -перехода можно записать в виде
где коэффициент I0 называется тепловым током:
Подставив сюда pn 0 и np 0 из (1.10), выражение (2.22) можно записать в виде
Тепловой ток сильно зависит от температуры. Основной вклад в эту зависимость вносит множитель ni2. С учетом (1.7) формулу (2.23) можно записать в виде
где множитель I00 слабо зависит от температуры, и в первом приближении этой зависимостью можно пренебречь.
|


 ,
, – диффузионная длина, это среднее расстояние, на которое успевают диффундировать носители за время жизни tp.
– диффузионная длина, это среднее расстояние, на которое успевают диффундировать носители за время жизни tp.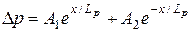
 ,
, 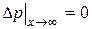 .
. . (2.17)
. (2.17) (2.18)
(2.18) . (2.19)
. (2.19)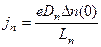 , (2.20)
, (2.20)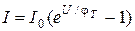 , (2.21)
, (2.21)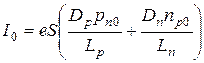 . (2.22)
. (2.22) (2.23)
(2.23) , (2.24)
, (2.24)


