Электронно-дырочный переход в равновесном состоянии.
ЭЛЕКТРИЧЕСКИЕ ПЕРЕХОДЫ 2.1. ЭЛЕКТРОННО-ДЫРОЧНЫЙ ПЕРЕХОД
Электронно-дырочный переход (p-n- переход) – тонкий переходной слой, образующийся между двумя областями кристалла с разным типом проводимости. Этот слой обеднен носителями заряда и обладает высоким удельным сопротивлением. Металлургической границей называется поверхность, разделяющая p- и n- области Различают резкий p-n- переход и плавный. В резком переходе тип проводимости резко (ступенчато) меняется на металлургической границе. В плавном переходе один тип проводимости плавно переходит в другой, металлургической границей считается поверхность, где Na=Nd. Переходы бывают симметричные (Na) p= (Nd) n и несимметричные (Na) p¹;(Nd) n. Когда концентрации отличаются на 2-3 порядка, переход называется односторонним, концентрация носителей в сильнолегированной области обозначается индексом «+»: p+-n или n+-p. В этом случае сильнолегированная область называется эмиттером, слаболегированная – базой.
Электронно-дырочный переход в равновесном состоянии.
Контактная разность потенциалов. При создании контакта двух областей с разной концентрацией носителей возникает диффузия носителей в область, где их концентрация меньше: дырки диффундируют из p- области в n- область, электроны – обратно. Здесь они рекомбинируют с основными носителями и исчезают. В результате образуется слой, обедненный носителями заряда, в котором заряд ионов акцепторных и донорных примесей не компенсирован (рис. 2.1). Этот объемный заряд создает электрическое поле E, которое препятствует дальнейшей диффузии носителей. При равновесии ток отсутствует, т.е. должны выполняться условия: jn = en m nE + eDn (dn/dx)=0, jp = ep m pE - eDp (dp/dx). (2.1) При этом возникает контактная разность потенциалов, которую легко найти их этих выражений, выразив напряженность E через градиент потенциала U: E=-dU/dx.
Используя соотношение Эйнштейна Dp= j T×;m p, получаем
Интегрирование дает
где нулевым индексом обозначены равновесные значения концентрации в соответствующих областях. Аналогично, jк выражается через концентрацию электронов:
С учетом того, что в области рабочих температур pp 0» Na, и pn 0» ni2/Nd, выражение (2.2) можно записать в виде
Следует отметить, что при выводе этих формул не использованы какие либо особенности структуры p-n- перехода, значение jк от них не зависит.
Концентрация основных носителей заряда резко падает при движении вглубь p-n- перехода, сравнивается с собственной концентрацией на металлургической границе, которая принята за начало координат, и далее уменьшается до концентрации неосновных носителей. Распределение носителей показано на рис.2.2 в логарифмическом (а) и линейном (б) масштабе. Строго говоря, границы перехода несколько размыты, но обычно рассматривается идеальная модель с резкими границами, считая, что на этих границах концентрация носителей резко падает до нуля. Распределение плотности заряда r в этой модели показано на рис.2.2 г. Плотности заряда в p- и n- областях обедненного слоя (толщиной dp и dn, соответственно) постоянны и равны r =-eNa, в области -dp<x<;0, (2.4 а) r =eNd, в области 0 <x<dn. (2.4 б) p-n- переход в целом электронейтрален, заряды в этих областях равны: q=eNa d p= eNd d n (2.5) Отношение dp/dn=Nd/Na, толщина p-n- перехода d = d p+ d n, отсюда
Напряженность электрического поля E можно найти из одномерного уравнения Пуассона
где U – потенциал, e – диэлектрическая проницаемость, e0 – диэлектрическая постоянная. С учетом того, что dU/dx=-E, и выражений (2.4) это уравнение записывается в виде
Интегрируя при граничных условиях
Максимальная напряженность достигается на металлургической границе:
Знак “–“ здесь показывает, что поле направлено противоположно координате x. Далее в области напряженность поля спадает по линейному закону до нуля (рис.2.2 д). Потенциал U(x) получается интегрированием функции E(x) и описывается квадратичной функцией (рис.2.2 е). Контактная разность потенциалов, очевидно, равна площади треугольника на рис.2.2 д:
Отсюда находим толщину p-n- перехода в равновесном состоянии:
Для резко несимметричного перехода одной из составляющих dp и dn можно пренебречь, практически весь переход располагается в слаболегированной области – базе, формула (2.12) при этом упрощается:
где N – концентрация легирующей примеси в базе. В таблице 2.1 приведены примеры, позволяющие судить о порядке величин jк, Emax и d (Т =300 К).
Таблица 2.1
|


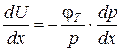 .
.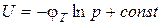 , отсюда контактная разность потенциалов jк равна
, отсюда контактная разность потенциалов jк равна , (2.2 а)
, (2.2 а)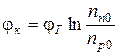 . (2.2 б)
. (2.2 б)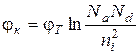 (2.3)
(2.3) Распределение носителей, электрического поля и потенциала в резком
Распределение носителей, электрического поля и потенциала в резком  ,
, 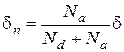 (2.6)
(2.6) , (2.7)
, (2.7) и
и 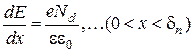 (2.8)
(2.8)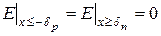 , получаем для p- области линейную функцию:
, получаем для p- области линейную функцию: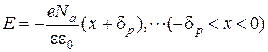 (2.9)
(2.9) . (2.10)
. (2.10)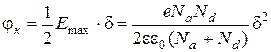 . (2.11)
. (2.11) (2.12)
(2.12)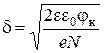 , (2.12 а)
, (2.12 а)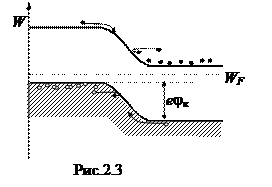 Энергетическая диаграмма p-n- перехода приведена на рис.2.3. Уровень Ферми одинаков для всей равновесной системы. Между областями существует потенциальный барьер, равный ejк. Основные носители, движущиеся к переходу, отражаются обратно, т.к. поле в переходе для них является тормозящим. Лишь ничтожная часть их имеет энергию W>ejк, достаточную для преодоления потенциального барьера. Неосновные носители свободно проходят через переход, для них электрическое поле является ускоряющим. Для наглядности можно представить электроны как тяжелые шарики, катящиеся по дну зоны проводимости, а дырки – как легкие пузырьки катящиеся, по потолку валентной зоны.
Энергетическая диаграмма p-n- перехода приведена на рис.2.3. Уровень Ферми одинаков для всей равновесной системы. Между областями существует потенциальный барьер, равный ejк. Основные носители, движущиеся к переходу, отражаются обратно, т.к. поле в переходе для них является тормозящим. Лишь ничтожная часть их имеет энергию W>ejк, достаточную для преодоления потенциального барьера. Неосновные носители свободно проходят через переход, для них электрическое поле является ускоряющим. Для наглядности можно представить электроны как тяжелые шарики, катящиеся по дну зоны проводимости, а дырки – как легкие пузырьки катящиеся, по потолку валентной зоны.


