Теория прочности грунтов и её практическое использование
5.1 Общие сведения.
Сдвиги всегда вызываются касательными напряжениями τп, возникающими в массиве от внешних нагрузок и собственного веса грунта. Им противодействуют силы сопротивления τ;, являющиеся в сущности силами трения, зависящими от качеств грунта и от нормальных напряжений σп к поверхности сдвига. Сложность проблемы в том, что форма и положение поверхностей сдвига не могут быть указаны, их нужно отыскивать. Для этого разработаны различные приемы, основу которых составляют параметры сопротивления грунтов сдвигу и результаты анализа предельного напряженного состояния грунтов в точках. При самостоятельном изучении раздела рационально придерживаться следующей логической последовательности: 1. методы определения параметров сопротивления грунтов сдвигу; 2. критические нагрузки на грунты основания 3. давление грунтов на подпорные сооружения; 4. оценка устойчивость откосов связного грунта; 5. определение прочности оснований фундаментов. Закономерности и параметры сопротивления грунтов сдвигу изучается по данным лабораторных и полевых испытаний. В лабораторных опытах обычно используется установка (рис. 5.2), позволяющая моделировать сдвиг в грунтовом массиве. Основной частью конструкции установки является кольцо, разделенное на верхнюю и нижнюю части, одна из которых неподвижна. Образец грунта в кольце помощью загрузочного устройства нагружается вертикальной силой N, которая равномерно распределяется через жесткий штамп. Величина передаваемого на грунт давления равна р = N / А (5.1) где А – площадь поперечного сечения кольца.
τ; = Т / А (5.2)
Исследованиями установлено, что ломаная линия без особой погрешности может быть заменена прямой, уравнение которой в принятых на рисунке обозначениях имеет вид: τ; = с + tgφ р (5.3) где с – ордината пересечения наклонной прямой с вертикальной осью; φ – угол наклона прямой к горизонтальной оси. Значения с и tgφ; определяют методом наименьших квадратов:
где п – количество опытов; j – номер опыта, в котором при заданном рj находят τj. Параметры с и угол наклона φ; в уравнении (5.3 ) являются эмпирическими коэффициентами, которые называют соответственно сцепление и угол внутреннего трения. Поскольку они характеризуют прочность грунтов, то считаются прочностными показателями. У сыпучих грунтов сцепление близко к нулю и по формуле (5.4) его обычно не вычисляют. У сыпучих грунтов сцепление близко к нулю и его обычно не вычисляют. При сцеплении равном нулю формула (5.3) имеет вид: τ; = tgφ р (5.6) Водонасыщенные глинистые грунты при загружении вертикальным давлением медленно уплотняются вследствие малой скорости движения выдавливаемой из мелких пор воды. Вследствие этого давление от внешней нагрузки разделяется на давление, передаваемое на твердые частицы (эффективное давление рэ), и давление, передаваемое на воду в порах (нейтральное давление рω). Для любого момента времени р = рэ + рω. Эффективное давление рэ уплотняет грунт, а под действием нейтрального давления рω происходит выдавливание воды из пор. Соотношение между ними может быть самым различным и со временем меняется. На практике обычно рассматривают два состояния, когда считают, что всё давление передается или только на воду или только на твердые частицы. Для первого случая справедливо равенство р = рω. Поскольку вода не может сопротивляться сдвигу, то tgφ×рω= 0 и формула (5.3) принимает вид τ; = с (5.7) Из образцов, испытываемых по такой схеме, называемой неконсолидированным недренированным сдвигом (НН), при приложении вертикальной нагрузки из образца не допускается отжатие воды. Во втором случае, называемым консолидированным дренированным сдвигом (КД), при загружении образца давлением р происходит свободное отжатие воды из грунта и зависимость между касательным и нормальным давлениями описывается уравнением (5.3).
Значения прочностных характеристик с 11и tgφ;11 используют при расчетах оснований по второй группе предельных состояний (по деформациям). Значения с 1 и tgφ;1 используют при расчетах оснований и грунтовых массивов по прочности. 5.2. Анализ предельного напряженного состояния грунтов в точке. Уравнение Кулона (5.3) можно применять, когда известно очертание поверхностей сдвига и найдены действующие по ним напряжения от внешних сил σп и τп. В действительности возможностей указать положение поверхности сдвига в грунтовом массиве и найти напряжения по ним не существует. Преодолеть данную сложность позволяет метод Мора, дополненный решениями Кулона. Теория Мора дает возможность по известным величинам главных напряжений изучать напряженное состояние в точке. Для решения практических задач достаточно знать наибольшее σ1 и наименьшее σ3 главные напряжения по двум главным площадкам при плоском напряженном состоянии. В дальнейших рассуждениях будем исходить из того, что в точках, принадлежащих поверхности сдвига, σ1 и σ3 найдены. Определение по ним напряжений σп и τп облегчаются графическими построениями на рис. 5.5.
Из теории известно, что напряжения по любой площадке являются координатами соответствующей на круге Мора точки. В рассматриваемой ситуации такая точка с координатами σп и τп является общей для круга Мора и прямой Кулона, проведенной под углом φ через ординату с для связного грунта (рис. 5.5 а) или из начала координат для сыпучего грунта (рис. 5.5 b). Из этого вытекает, что прямая Кулона является касательной к кругу Мора в точке b. Её уравнение из рассмотрения прямоугольных треугольников о'ba (для случая а) и оba (для случая b), принимая во внимание, что радиус круга Мора равен ab=(σ;1 - σ;3 )/ 2, приводится к виду: для связного грунта: sin φ= для сыпучего грунта: sin φ= Выражения (5.8) и (5.9) называют условиями предельного напряженного состояния в точке соответственно связного и сыпучего грунта. Они сложнее уравнения Кулона, но удобнее при разработке инженерных методов расчетов. Суть приемов заключается в том, что вместо σ;1 и σ;3, являющихся функциями некоторых аргументов, подставляются выражения для их определения и производятся необходимые преобразования. При выводе выражения для нахождения расчетного сопротивления грунта R в условие (5.8) подставляются известные формулы для определения обеих главных напряжений σ;1 и σ3 от равномерно распределенной нагрузки. При разработке теории давления грунтов на подпорные сооружения известно выражение для одного из главных напряжений. Другое главное напряжение приходится находить из условий (5.8) или (5.9). Главные напряжения не удается определять при анализе устойчивости откосов выемок и оценке прочности оснований фундаментов, нагруженных различными видами нагрузок (вертикальными и горизонтальными силами, моментами). В методах оценки устойчивости откосов отыскивается положение поверхности сдвига, и затем проверяются условия равновесия. Основу расчетов прочности оснований составляют задаваемые вероятные очертаний поверхностей сдвига и установленные по ним напряжения. 5.3. Критические нагрузки на грунты основания
Расчетное сопротивление может устанавливаться различными способами. На практике при проектировании фундаментов оно вычисляется по формуле R= где g с1 и g с2 – коэффициенты условий работы, принимаемые по табл.5.1; к – коэффициент, принимаемый в контрольной работе к =1; Таблица 5. 1 Значения коэффициентов g с1 и g с2
Примечания: 1. Для зданий с гибкой конструктивной схемой значение коэффициента gс2 принимается равным 1. 2. При промежуточных значений L / H коэффициент gс2 определяется по интерполяции. 3. К сооружениям с жесткой конструктивной схемой относятся здания, конструкции которых приспособлены к восприятию усилий от деформаций оснований. Мg, Mq, Мс – коэффициенты, принимаемые в зависимости от угла внутреннего трения грунтов под подошвой фундаментов по табл.5.2; Таблица 5.2 Значения коэффициентов Мg, Mq, Мс
b – ширина подошвы фундамента, в м; g II - удельный вес грунта, залегающего ниже подошвы фундамента, в кН/м3; g ı II – удельный вес грунтов, залегающих выше подошвы фундаментов, в кН/м3; d1 – глубина заложения фундаментов от поверхности грунта (при наличии подвала – от пола подвала); db – глубина подвала, равная расстоянию от уровня планировки до пола подвала (при глубине подвала свыше 2м принимается равной 2 м, а при ширине подвала свыше 20 м принимается d b=0); cII – расчетное значение удельного сцепления грунта, залегающего непосредственно под подошвой фундамента. При самостоятельном изучении курса вычислить расчетное сопротивление грунта по данным, приведенным в табл. 5.3. Схема залегания грунтовых слоев принимается по рис. 1, значения показателей для заданных грунтовых слоев берутся по табл. 2. Расчетное сопротивление определять для слоя, на который при заданной глубине заложения подошвы будет опираться фундамент. Содержание задания. Вычислить расчетное сопротивление грунта основания: 1 – для здания без подвала (рис. 5.7). Глубину заложения фундамента от поверхности d1 принять по табл. 5.3, номер ИГЭ и значения характеристик грунтов принять по таблицам 1 и 2. 2 – для здания с подвалом (рис. 5.8). Глубину подвала и глубину заложения фундамента от его пола принять по табл. 5.3. Конструктивную схему здания считать жесткой. Таблица 5.3 Исходные данные для определения расчетного сопротивления грунтов
Примечание. Для вариантов 1-10 данные указаны в числителе, для вариантов 11-20 данные приведены в знаменателе. Пример 1. Определить расчетное сопротивление грунта при следующих данных: здание без подвала (рис. 5.7), глубина заложения фундамента d1=2м, ширина подошвы b=1.5 м.
По табл. 5.1 при IL=0.33 gс1=1.2, gс2=1.1. По табл. 5.2 при jII=160 Мg=0.36, Mq=2.43, Мс=4.99. Под подошвой и выше подошвы фундамента находится один и тот же грунт: γII = γ' II =19.5 кН/м3. Поскольку подвала нет, то db=0. R= γс1 γс2 [ Мg b g II+Mq d1 g ı II +Mc cII ] = 1.2 * 1.1 [ 0.36 * 1.5 * 19.5+2.43 * 2 * 19.5+4.99 * 43 ] =422 кПа. Пример 2. Здание с подвалом: db =1.5 м, d1=0.5 м, грунтовые условия те же, расчетная схема фундамента на рис. 5.8.
+ (2.43-1)* 1.5 * 19.5+4.99 * 43 ] =383 кП а. Указание. Выявить, насколько (в %) вычисленное расчетное сопротивление зависит от ширины подошвы (первого слагаемого в скобках). Выяснить, какое влияние на расчетное сопротивление грунта оказывает устройство подвала.
Иным способом установления расчетного сопротивления является назначение его величины по показателям физического состояния грунтов. Для этого составлены таблицы, имеющиеся в СНиП 2.02.01-83* и СП 50-101-2004. Полезно знать, что в прошлом за допустимое давление на границе области линейного сжатия принимали давление р кр1 (рис. 5.6), затем им стали считать нормативное давление R н. В проектах того времени фундаменты проектировались по ним. На рис. 5.6 показано, что р кр1 и R н меньше R по формуле (5.10). Данное обстоятельство имеет практическое значение при реконструкции старых зданий. В случае увеличения нагрузок на фундаменты давления на грунты можно повышать до расчетного сопротивления R по формуле (5.10). Другим критическим давлением является предельное давление ри (рис. 5.6), означающее нарушение прочности грунта. В этот момент в основании образуются поверхности сдвига, по которым грунт под действием касательных напряжений перемещается из-под фундамента как, например, на рис. 5.1. Нарушения прочности можно ожидать в основном от горизонтальных нагрузок, вызывающих появление в основании относительно больших, в сравнении с вертикальными напряжениями, касательных напряжений. Положение и форму поверхности сдвига, действующие по ней нормальные и касательные напряжения отыскивать сложно. Методы расчета несущей способности (прочности) снований базируются на поиске вероятной поверхности скольжения, форма которой должна быть как статически, так и кинематически возможной при передаваемых на фундаменты воздействиях. Различают сдвиг по подошве фундамента (плоский сдвиг) и сдвиг по образующейся в основании криволинейной поверхности (глубинный сдвиг). Схема сдвига выбирается по результатам проверки специального условия. Реактивные давления по подошве фундаментов при нарушении прочности основания в общем случае распределяются неравномерно. За несущую способность основания, поэтому, принимают равнодействующую предельного сопротивления основания или её составляющую. Условия, при которых нужна проверка прочности основания, указаны в нормах проектирования СНиП 2.02.01-83*. 5.4. Давление грунтов на подпорные сооружения. К подпорным сооружениям относятся конструкции, удерживающие откосы выемок или насыпей от обрушения. Ими являются стены подвалов и подземных сооружений, подпорные стенки, применяющиеся в различных областях строительства. Конструктивные элементы подпорных стенок показаны на рис. 5.9.
Различают два случая работы стенки. К первому относится случай, когда стенка удерживает откос от обрушения. От засыпки на заднюю грань передается давление, называемое активным давлением (рис. 5.10 а), которое стремиться сдвинуть стенку. При смещении стенки в засыпке формируется область обрушения в форме клина, называемая призмой обрушения, а наклонная поверхность скольжения, по которой она смещается вниз, в инженерных расчетах
принимается за плоскость обрушения. Стенка смещается в сторону откоса (рис. 5.10 b). При этом возникает отпор грунта засыпки. С увеличением смещения внутри откоса образуется наклонная поверхность, по которой грунт подобно клину выдавливается вверх. Поверхность скольжения становится поверхностью выпора, а выдавливаемый грунт понимается как призма выпора. Отпор грунта в момент образования в засыпке поверхности выпора называют пассивным давлением или пассивным отпором. В обоих случаях принимается, что засыпка находится в состоянии предельного напряженного состояния. Следовательно, в любой точке засыпки будут справедливы условия (5.8) и (5.9). Одно из главных напряжений в этих выражениях возникает по горизонтальной площадке от собственного веса грунта. При активном давлении это наибольшее главное напряжение σ1, а при пассивном отпоре наименьшее главное напряжение σ3 (рис. 5.10). Другое главное напряжение находят при преобразовании условий (5.8) или (5.9). Активным давлением является главное напряжение σ3, а пассивным отпором становится σ1. Выражения для их определения выводятся при проведении несложных преобразований. С глубиной активное давление и пассивный отпор увеличиваются. При расчете подпорной стенки они рассматриваются как распределенная внешняя нагрузка. 5.5. Устойчивость откосов связного грунта. При устройстве глубоких выемок вертикальные откосы связного грунта могут сползать вниз. Для безопасного проведения работ стенки котлованов нужно делать пологими. Такая же трудность возникает при устройстве насыпей. Цель состоит в определении угла наклона стенки выемки или насыпи, при которой откос делается устойчивым.
Вопросы для самопроверки.
1. Как происходит нарушение прочности грунтов. 2. Какие испытания проводят для изучения сопротивления грунтов сдвигу. 3. Какими параметрами характеризуется сопротивление грунтов сдвигу. 4. Как определяют расчетные значения сцепления и угла внутреннего трения. 5. Какие значения прочностных характеристик используют в расчетах оснований по деформациям и по прочности. 6. Что означает по смыслу расчетное сопротивление?. 7. Как происходит нарушение прочности основания при плоском сдвиге и при глубинном сдвиге? 8. Как возникает активное давление грунта на подпорную стенку? 9. Как возникает пассивное давление грунта на подпорную стенку? 10. Какие допущения составляют основу расчета устойчивости откосов связного грунта?
Литература
1. Ухов С. Б., Семенов В. В., Знаменский В. В. и др. Механика грунтов, основания и фундаменты.- 2-е изд. – М.: Высш. шк., 2002. 2. Берлинов М. В. Основания и фундаменты. – М.: Высш. шк..,1998. 3. Швецов Г. И. Инженерная геология, механика грунтов, основания и фундаменты. – М.; Высш. школа. 1997 г. 4. СНиП 2.02.01-83* Основания зданий и сооружений. 5. ГОСТ 12248-96. Грунты. Методылабораторного определения характеристик прочности и деформируемости. 6. ГОСТ 20276-99. Грунты. Методыполевого определения характеристик прочности и деформируемости. 7. ГОСТ 20592-96. Грунты. Методы статистической обработки результатов испытаний.
|

 По наблюдениям нарушение прочности оснований происходит в результате смещения фундаментов по плоской (по подошве фундамента) или сложной по виду криволинейной поверхности (глубинный сдвиг), как, например, на рис. 5.1, образующейся внутри грунтового массива. Изображенная схема упрощена, так как в действительности скольжение наблюдается по нескольким направлениям в пределах зон некоторой толщины, принимаемой за поверхности условно. Сходным образом возникает движение грунтов при потере устойчивости откосов выемок или насыпей. Под прочностью грунтов, таким образом, нужно понимать суммарное сопротивление сдвигу по всей поверхности сдвига. В инженерных расчетах обычно находят его составляющую, являющуюся проекцией на ту или иную ось, или момент относительно некоторой оси вращения.
По наблюдениям нарушение прочности оснований происходит в результате смещения фундаментов по плоской (по подошве фундамента) или сложной по виду криволинейной поверхности (глубинный сдвиг), как, например, на рис. 5.1, образующейся внутри грунтового массива. Изображенная схема упрощена, так как в действительности скольжение наблюдается по нескольким направлениям в пределах зон некоторой толщины, принимаемой за поверхности условно. Сходным образом возникает движение грунтов при потере устойчивости откосов выемок или насыпей. Под прочностью грунтов, таким образом, нужно понимать суммарное сопротивление сдвигу по всей поверхности сдвига. В инженерных расчетах обычно находят его составляющую, являющуюся проекцией на ту или иную ось, или момент относительно некоторой оси вращения. Подвижное кольцо (на рисунке верхнее) нагружается постепенно увеличивающейся горизонтальной нагрузкой Т и начинает смещаться. Осадка жесткого штампа и горизонтальное смещение кольца δ; измеряются индикаторами 5. В образце по плоскости между кольцами возникают касательные напряжения τ;, равные
Подвижное кольцо (на рисунке верхнее) нагружается постепенно увеличивающейся горизонтальной нагрузкой Т и начинает смещаться. Осадка жесткого штампа и горизонтальное смещение кольца δ; измеряются индикаторами 5. В образце по плоскости между кольцами возникают касательные напряжения τ;, равные
 (5.4)
(5.4)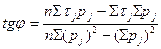 (5.5)
(5.5) Для любого выделяемого однородного слоя (ИГЭ) число определяемых пар значений сi и tgφi должно быть не менее шести. На сдвиг, следовательно, должно быть испытано не менее 18 образцов. Согласно ГОСТ 20522-96 сi и tgφi рассматриваются как отдельные характеристики, изменяющиеся случайным образом. Статистическая обработка значений сi и tgφi проводится в последовательности, изложенной в приложение 2. Параметром Х в формулах являются вычисленные из выражений (5.4) и (5.5) величины сi и tgφi. Для них устанавливаются нормативные значения сп и tgφп, коэффициенты надежности по грунту gg при доверительных вероятностях α1 = 0.95 и α11 = 0.85, расчетные значения прочностных показателей с1 и tgφ1 при доверительной вероятности α1 = 0.95, расчетные значения с 11и tgφ;11 при доверительной вероятности α11 = 0.85. По значениям tgφ;1 и tgφ;11 определяют углы внутреннего трения φ;1 и φ;11. На графике (рис. 5.4) им соответствуют три наклонных прямых, взаимное расположение которых связано с результатами расчетов.
Для любого выделяемого однородного слоя (ИГЭ) число определяемых пар значений сi и tgφi должно быть не менее шести. На сдвиг, следовательно, должно быть испытано не менее 18 образцов. Согласно ГОСТ 20522-96 сi и tgφi рассматриваются как отдельные характеристики, изменяющиеся случайным образом. Статистическая обработка значений сi и tgφi проводится в последовательности, изложенной в приложение 2. Параметром Х в формулах являются вычисленные из выражений (5.4) и (5.5) величины сi и tgφi. Для них устанавливаются нормативные значения сп и tgφп, коэффициенты надежности по грунту gg при доверительных вероятностях α1 = 0.95 и α11 = 0.85, расчетные значения прочностных показателей с1 и tgφ1 при доверительной вероятности α1 = 0.95, расчетные значения с 11и tgφ;11 при доверительной вероятности α11 = 0.85. По значениям tgφ;1 и tgφ;11 определяют углы внутреннего трения φ;1 и φ;11. На графике (рис. 5.4) им соответствуют три наклонных прямых, взаимное расположение которых связано с результатами расчетов.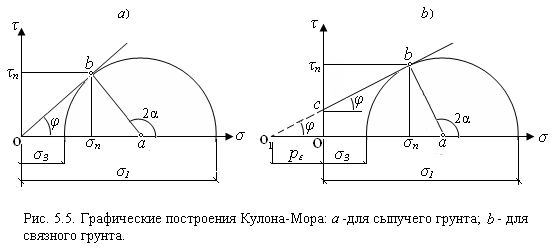
 (5.8)
(5.8)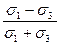 (5.9)
(5.9) Из критических нагрузок наиболее важным является понятие о давлении на границе области линейного сжатия (первое критическое давление), в пределах которой деформации грунтов оснований изменяются пропорционально увеличению нагрузки (рис. 5.6). По принятой терминологии его называют расчетным сопротивлением грунта R. При давлениях, не превышающих R, можно рассчитывать осадки оснований.
Из критических нагрузок наиболее важным является понятие о давлении на границе области линейного сжатия (первое критическое давление), в пределах которой деформации грунтов оснований изменяются пропорционально увеличению нагрузки (рис. 5.6). По принятой терминологии его называют расчетным сопротивлением грунта R. При давлениях, не превышающих R, можно рассчитывать осадки оснований. [ Мg b g II+ Mq d1 g ı II +(Mq -1) d b g ı II+ Mc c II] (5.10)
[ Мg b g II+ Mq d1 g ı II +(Mq -1) d b g ı II+ Mc c II] (5.10) Основанием является слой ИГЭ 4 со следующими характеристиками грунта: IL=0,33, прочностные показатели jII=160, cII =43 кПа определены по результатам непосредственных испытаний, к = 1, g =19.5 кН/м3, L/H =1.5.
Основанием является слой ИГЭ 4 со следующими характеристиками грунта: IL=0,33, прочностные показатели jII=160, cII =43 кПа определены по результатам непосредственных испытаний, к = 1, g =19.5 кН/м3, L/H =1.5.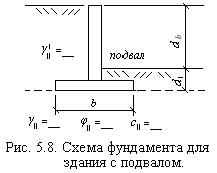 R= [ Мg b g II+Mq d1 g ıII + (Mq-1) dbg ıII+Mc cII ] = 1.2*1.1 [ 0.36 * 1.5 * 19.5+2.43 * 0.5 * 19.5+
R= [ Мg b g II+Mq d1 g ıII + (Mq-1) dbg ıII+Mc cII ] = 1.2*1.1 [ 0.36 * 1.5 * 19.5+2.43 * 0.5 * 19.5+ Грунт, удерживаемый стенкой в заданном положении, называют засыпкой. При нарушении равновесия откоса в засыпке образуется в общем случае криволинейная поверхность сдвига, которую называют поверхность сдвига. Поверхность стенки, на которую передается давление засыпки, считают задней гранью.
Грунт, удерживаемый стенкой в заданном положении, называют засыпкой. При нарушении равновесия откоса в засыпке образуется в общем случае криволинейная поверхность сдвига, которую называют поверхность сдвига. Поверхность стенки, на которую передается давление засыпки, считают задней гранью.
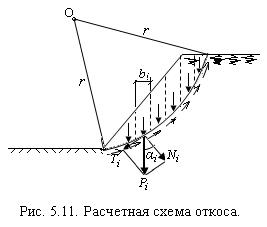 В основу расчетного метода положены данные полевых наблюдений. Предполагается, что потеря устойчивости откоса заданной крутизны происходит в результате сдвига некоторой массы грунта по криволинейной поверхности, форма которой принимается круглоцилиндрической. По характеру движение представляет вращение смещающегося объёма грунта по дуге окружности радиусом r относительно некоторого центра О (рис. 5.11). Смещающийся массив считается твердым телом, разделенным для удобства вычислений на отсеки шириной bi. Вес каждого отсека Рi заменяется вертикальной силой, которая в точке пересечения с дугой скольжения раскладывается на нормальную Ni и касательную T i составляющие. Касательная составляющая веса отсеков Тi с плечом r создает сдвигающий момент Msa относительно центра вращения О. Удерживающие силы в пределах каждого отсека обусловлены сопротивлением сдвигу, которые можно определить с использованием формулы (5.3). С плечом r относительно центра вращения О они создают удерживающий момент Мsr. Устойчивость откоса характеризуется коэффициентом запаса устойчивости kst, равным отношению момента Мsr к моменту Msa. Сложность в том, что для его нахождения положение центра вращения однозначно указать невозможно. Оно отыскивается внутри некоторой области методом последовательного приближения. Наиболее вероятно то положение центра О, при котором значение коэффициента запаса устойчивости kst станет минимальным. Откос считается устойчивым, если минимальное значение kst будет не менее нормируемой величины.
В основу расчетного метода положены данные полевых наблюдений. Предполагается, что потеря устойчивости откоса заданной крутизны происходит в результате сдвига некоторой массы грунта по криволинейной поверхности, форма которой принимается круглоцилиндрической. По характеру движение представляет вращение смещающегося объёма грунта по дуге окружности радиусом r относительно некоторого центра О (рис. 5.11). Смещающийся массив считается твердым телом, разделенным для удобства вычислений на отсеки шириной bi. Вес каждого отсека Рi заменяется вертикальной силой, которая в точке пересечения с дугой скольжения раскладывается на нормальную Ni и касательную T i составляющие. Касательная составляющая веса отсеков Тi с плечом r создает сдвигающий момент Msa относительно центра вращения О. Удерживающие силы в пределах каждого отсека обусловлены сопротивлением сдвигу, которые можно определить с использованием формулы (5.3). С плечом r относительно центра вращения О они создают удерживающий момент Мsr. Устойчивость откоса характеризуется коэффициентом запаса устойчивости kst, равным отношению момента Мsr к моменту Msa. Сложность в том, что для его нахождения положение центра вращения однозначно указать невозможно. Оно отыскивается внутри некоторой области методом последовательного приближения. Наиболее вероятно то положение центра О, при котором значение коэффициента запаса устойчивости kst станет минимальным. Откос считается устойчивым, если минимальное значение kst будет не менее нормируемой величины.


