Основные расчетные модели грунтов
Требования к расчетным моделям Точность прогнозов в механике грунтов в большой степени определяется тем, с какой полнотой в уравнениях состояния отражаются особенности деформирования грунтов. При этом в практике проектирования для конкретных случаев используются расчетные модели грунта разной сложности. Для широкого круга задач строительства оказалось возможным выделить те, где основной является оценка несущей способности (прочности и устойчивости) грунтов. Напротив, в других задачах наиболее важным будет прогноз деформаций основания и сооружения. Наконец, в некоторых задачах необходимы и оценка несущей способности, и прогноз деформаций грунтов. Однако эти расчеты можно проводить раздельно, что позволило распространить на расчеты оснований общие принципы расчетов по предельным состояниям: · расчет по несущей способности (потеря устойчивости; хрупкое, вязкое или иного характера разрушения грунта; чрезмерные пластические деформации или деформации неустановившейся ползучести); · расчет по деформациям (достижение состояния, затрудняющего нормальную эксплуатацию сооружения или снижающего его долговечность вследствие недопустимых перемещений – осадок, разности осадок, кренов и т. п.). Существо расчетов по первой группе предельных состояний заключается в том, что расчетная нагрузка на основание не должна превышать силу предельного сопротивления грунтов основания. По второй группе предельных состояний совместная деформация сооружения и основания не должна превышать предельной для конструктивной схемы данного сооружения. Такой подход обусловил возможность использования наиболее простых расчетных моделей грунтов: для расчетов конечных напряжений и стабилизированных осадок – теории линейного деформирования грунта; для расчетов развития осадок во времени – теории фильтрационной консолидации грунта; для расчетов несущей способности, прочности, устойчивости и давления грунта на ограждения – теория предельного напряженного состояния грунта.
Модель теории линейного деформирования грунта Применимость этой модели к грунтам была впервые обоснована трудами Н. П. Пузыревского, К. Терцаги, Н. М. Герсеванова, В. А. Флорина, Н. А. Цытовича. Эта модель наиболее распространена в инженерной практике благодаря своей простоте и возможности использования хорошо разработанного математического аппарата теории упругости для описания напряженно-деформированного состояния грунтов. Теория линейного деформирования грунта базируется на предположении, что при однократном нагружении (или разгрузке) зависимость между напряжениями и деформациями в грунтах линейна. Кроме того, при нагружении рассматривается лишь общая деформация грунта без разделения ее на упругую и пластическую составляющие. Первое допущение обеспечивает возможность использования для расчетов напряжений в массиве грунта аппарата теории упругости, а второе – при известных напряжениях рассчитывать конечные деформации основания. Использование теории линейного деформирования грунта всегда требует установления предела ее применимости. Уравнения состояния модели теории линейного деформирования записываются в виде обобщенного закона Гука:
где Теорию линейного деформирования иногда называют теорией упругости грунтов. Формально это справедливо, так как она использует математический аппарат теории упругости. Однако нужно иметь в виду, что это сходство чисто формальное, так как теория линейного деформирования рассматривает общие деформации, не разделяя их на упругие и пластические. Кроме того, нагружение и разгрузка грунта в теории линейного деформирования происходят по разным законам и описываются различными по величине характеристиками деформируемости грунта.
Модель теории фильтрационной консолидации В наиболее простой постановке теория описывает деформирование во времени полностью водонасыщенного грунта (грунтовой массы). Принимается, что полное напряжение, возникающее в элементе грунта от приложенной нагрузки, разделяется на напряжения в скелете грунта (эффективные напряжения) и давление в поровой воде (поровое давление). В различных точках массива грунта под действием нагрузки возникают разные значения порового давления. Вследствие этого образуется разность напоров в поровой воде и происходит ее отжатие в менее нагруженные области массива. Одновременно под действием эффективных напряжений происходят перекомпоновка частиц и уплотнение грунта. Математическое описание этого процесса базируется на основной предпосылке о неразрывности среды, сформулированной академиком Н. Н. Павловским еще в 1922 г., т. е. считается, что уменьшение пористости грунта (его уплотнение) пропорционально расходу воды (оттоку воды из пор грунта). Следствием этого является важное положение о том, что скорость деформации грунта будет находиться в прямой зависимости от скорости фильтрации в нем поровой воды. Поэтому основной характеристикой грунта, определяющей время протекания процесса фильтрационной консолидации, является коэффициент фильтрации. В теории фильтрационной консолидации скелет грунта принимается линейно деформируемым. Следует отметить, что в инженерной практике используются и более сложные модели теории консолидации, учитывающие трехкомпонентный состав грунта, сжимаемость поровой воды, ползучесть скелета и другие процессы, возникающие в грунте при его деформациях. Такие модели описаны в трудах Н. М. Герсеванова, В. А. Флорина, М. А. Био, Ю. К. Зарецкого, З. Г. Тер-Мартиросяна и других ученых.
Модель теории предельного напряженного состояния грунта Данная модель относится только к предельному состоянию, т. е. к такому напряженному состоянию, когда в массиве грунта от действующих нагрузок сформировались значительные по размерам замкнутые области, в каждой точке которых устанавливается состояние предельного равновесия. Потому теорию предельного напряженного состояния часто называют теорией предельного равновесия грунта. Теория предельного равновесия грунта позволяет определить предельную нагрузку на основание (его предельная несущая способность), но при этом невозможно определить деформации грунта. Решения теории предельного равновесия используются также для общих расчетов устойчивости сооружений и оснований, откосов и склонов, определения давления грунта на ограждения. В основе современных решений теории предельного равновесия лежат фундаментальные работы В. В. Соколовского.
Теории нелинейного деформирования грунтов Теории нелинейного деформирования грунтов применяются для расчетов напряженно-деформированного состояния и оценки прочности оснований и грунтовых сооружений, когда связь между напряжениями и деформациями существенно нелинейна, поэтому они часто называются теориями пластичности грунтов. Значительное распространение в инженерной практике получила деформационная теория пластичности, основанная на теории малых упругопластических деформаций академика А. А. Ильюшина. В наиболее простом виде эта теория исходит из допущения, что объемная и сдвиговая деформации зависят только соответственно от среднего нормального напряжения и интенсивности касательных напряжений, т. е. Различные модификации теорий нелинейного деформирования грунтов представлены в работах С. С. Вялова, А. Л. Гольдина, Ю. К. Зарецкого, А. Л. Крыжановского, В. Г. Федоровского, В. И. Соломина, В. Г. Николаевского и др.
|

 ;
;  ;
; ;
;  ;
; ;
;  ,
, – модуль общей линейной деформации;
– модуль общей линейной деформации; 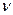 – коэффициент поперечного линейного расширения (коэффициент Пуассона).
– коэффициент поперечного линейного расширения (коэффициент Пуассона).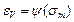 ;
; 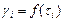 . Однако деформационная теория пластичности не учитывает некоторые процессы, происходящие в грунте. Более точные решения можно получить с помощью теории пластического течения. Однако это приводит к усложнению экспериментов для определения параметров уравнения состояния и расчетного аппарата анализа. Теорию пластического течения применяют при решении сложных задач гидротехнического строительства.
. Однако деформационная теория пластичности не учитывает некоторые процессы, происходящие в грунте. Более точные решения можно получить с помощью теории пластического течения. Однако это приводит к усложнению экспериментов для определения параметров уравнения состояния и расчетного аппарата анализа. Теорию пластического течения применяют при решении сложных задач гидротехнического строительства.


