Определение напряжений в массиве грунта при действии единичной вертикальной силы N, приложенной к границе грунтового основания.
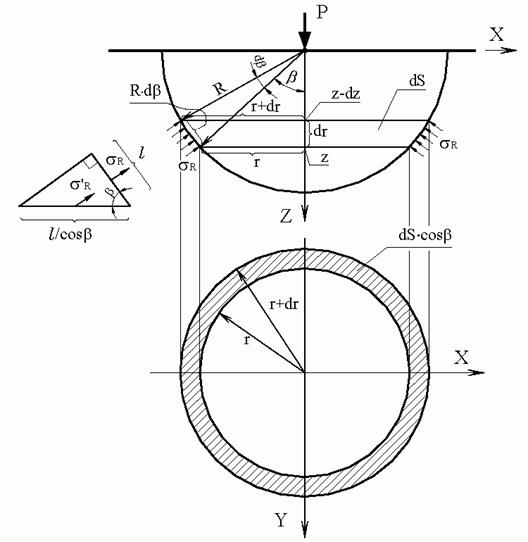
Решение задачи Буссинеска. Основано на следующих гипотезах (впоследствии подтвержденных точными решениями): а) нормальные напряжения на площадках, касательных к сферической поверхности с центром в точке приложения силы, являются главными напряжениями. По этой причине касательные напряжения на указанных площадках отсутствуют; б) нормальные напряжения, лежащие в вертикальной плоскости, на площадках, нормальных к сферической поверхности с центром в точке приложения силы, равны нулю; в) нормальные напряжения на площадках, касательных к сферической поверхности с центром в точке приложения силы, прямо пропорциональны косинусу угла видимости и обратно пропорциональны квадрату радиуса сферы. Под углом видимости понимается угол между радиусом сферы, проведенным в центр площадки, и центральной вертикальной осью сферы. Постулированные гипотезы позволяют получить замкнутые аналитические решения о распределении напряжений в полупространстве от действия вертикальной силы на его границе, основанные исключительно на уравнениях равновесия. Решение задачи поясняется графическими построениями на рис. 4.5, на котором представлены вертикальный разрез полупространства и его сечения горизонтальными плоскостями. Начало прямоугольной декартовой системы координат разместим в точке приложения вертикальной силы Р на границе полупространства. Ось z направим по вертикали вниз, ось x – по горизонтали вправо, а ось y – перпендикулярно плоскости чертежа. Относительно начала осей координат построена полусфера радиусом R, пересечение которой с вертикальной плоскостью, проходящей через центральную ось, образует полуокружность такого же радиуса. В сечении полусферы горизонтальной плоскостью на глубине z образуется окружность радиусом r. Угол видимости радиуса r на вертикальном разрезе обозначим β.
Рис. 4.5. Графическое построение к решению задачи Буссинеска
Условие равновесия:
В соответствии с гипотезой в), σR = A cosβ/ R 2. Кроме этого, r = R ⋅ sinβ. Подставляя в уравнение (3.1) выражения для σR и r и выполняя преобразования, получим:
Выполняем замену переменных в уравнении (4.2): u = cosβ, du = − sinβ ⋅ d β. Продолжая преобразования, получим выражение для неопределенного коэффициента А:
Выразим cosβ через ординату z: cosβ = z / R. С учетом этого, формула для определения напряжения σR будет иметь вид
Практический интерес представляют напряжения на горизонтальной площадке, наклоненной к площадке, на которой действуют напряжения σR, под углом β. В соответствии с гипотезой б) главный вектор напряжений на горизонтальной площадке σ′R совпадает по направлению с вектором напряжения σR, а его модуль равен σ′R = σR ⋅ cosβ. Проекции главного вектора напряжений σ′R на координатные оси являются компонентами тензора напряжений на горизонтальной площадке. Поскольку главный вектор напряжений σ′R совпадает по направлению с радиусом вектором R, направляющие косинусы вектора напряжений определяются формулами:
С учетом полученных выше зависимостей, компоненты тензора напряжений на
Формулу для σz обычно табулируют. Для этого выполняют следующие преобразования:
В дальнейшем для практических расчетов расчетную схему задачи приводят к более простому виду (рис. 4.6). Вертикальные напряжения в расчетной точке М определяют по формуле
Z – глубина точки; r – расстояние от точки до линии действия силы; М – рассматриваемая точка; N – сосредоточенная вертикальная сила.
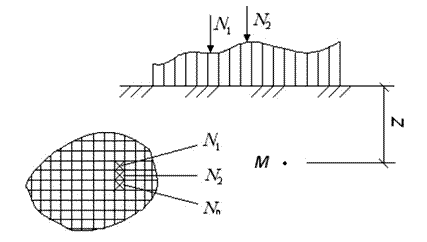
Определение напряжений в массиве грунта от действия нескольких вертикальных сосредоточенных сил, приложенных к границе грунтового основания (принцип Сен-Венана – принцип независимости действия сил).
Рис. 4.7. Схема к определению напряжений в массиве грунта от действия нескольких вертикальных сосредоточенных сил
Если к поверхности изотропного линейно-деформируемого полупространства приложено несколько сил (N 1, N 2,..., Nn), то при прямой пропорциональности между напряжениями и деформациями можно использовать принцип суперпозиции и найти значение σz в любой точке М простым суммированием:
Коэффициент К, зависящий от безразмерного параметра r/z, определяется так же как и в предыдущем случае. Определение напряжений σz в массиве грунта при действии любой распределенной нагрузки, приложенной к границе грунтового основания (метод элементарного суммирования). Пусть к поверхности изотропного линейно-деформируемого полупространства в пределах площади загружения приложено распределенное давление. Загруженную площадь можно разбить на небольшие прямоугольники и более сложные фигуры по ее контуру.
Рис. 4.8. Схема к определению напряжений в массиве грунтапри действии любой распределенной нагрузки
Определив величину szi от нагрузки каждой из небольших фигур, на которые разбита площадь загружения, и произведя суммирование этих напряжений, определим напряжение szi от действия распределенной нагрузки (аналогично формуле 4.9):
Этот метод также иногда называют методом элементарных квадратов. Коэффициент К, зависящий от безразмерного параметра r/z, определяется так же как и в предыдущих случаях. Точность расчета увеличивается с уменьшением размеров отдельных элементов, однако при большом числе элементов значительно увеличивается трудоемкость задачи.
|

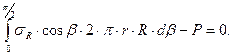 (4.1)
(4.1) (4.2)
(4.2)
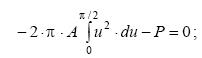
 ; (4.3)
; (4.3)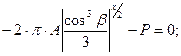

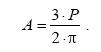
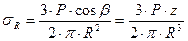 . (4.4)
. (4.4)

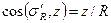 . (4.5)
. (4.5)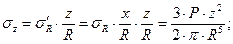
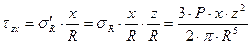 ; (4.6)
; (4.6)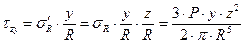 .
.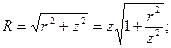 (4.7)
(4.7)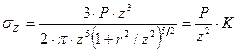 , (4.8)
, (4.8)

 .
.
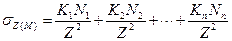 , (4.9)
, (4.9)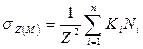 .
.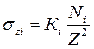 .
.
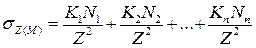 ,
, .
.


