Процеси росту та розчинення кристалів (масовий ріст та розчинення).
Процеси масового росту (розчинення) кристалів відбуваються в пересичених (ненасичених) розчинах. Динаміка масового росту (розчинення) кристалів описується диференціальним рівнянням, в якому функцією є сумарна маса кристалів G а аргументом час t. Це диференціальне рівняння має вигляд:
де k1, k2, k3 – коефіцієнти геометричної форми кристалів; V, g, α;, Динаміка лінійного розміру окремого кристала r є випадковою величиною, її можна описати наступним стохастичним диференціальним рівнянням Іто:
де Dr – похідна від дисперсії лічильного розподілу кристалів за їх лінійними розмірами; nr,s – випадкова величина, типу «білого шуму» - перша похідна від вінерівського випадкового процесу. Співвідношення, типу (4.9) – (4.11) є основою математичного опису (математичної моделі) процесів масового росту (розчинення) кристалів в процесі масової кристалізації.
|
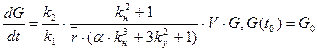, (4.9)
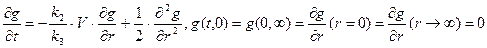, (4.10)
, r, kн, t – відповідно, питома швидкість масового росту (розчинення) кристалів, диференціальна функція їх лічильного розподілу за лінійними розмірами (полідисперсні кристали), коефіцієнт асиметрії лічильного розподілу кристалів за їх лінійними розмірами, середній лінійний розмір кристалів, лінійний розмір окремого кристала (випадкова величина), коефіцієнт лінійно-масової нерівномірності кристалів, час.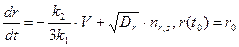
, (4.11)
