Напряжения от распределенной нагрузки (метод угловых точек)
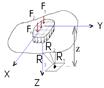
В случае действия распределенной нагрузки напряжение в массиве можно определить по формулам для нахождения напряжения при действии сосредоточенной силы, используя принцип суперпозиции (независимость действия сил) Область загружения делится на ряд элементов, распределенная нагрузка на которых заменяется равнодействующей в центрах их тяжести. σz=(3/2)*π* (F1Z13/R15 + F2Z23/R25 +…+ FnZn3/Rn5) или σz=∑(FiKi/Z2)
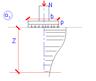
Решение для определения σz под центром площади выглядит как: σz=P*f*(z/(0.5b); a/b), где b- ширина подошвы, a-длинна подошвы фундамента, z – глубина на которой определяется напряжение, P- среднее давление под подошвой. Значение f приводится в СНиП 2.02.01-83*, в виде таблиц. В них по двум параметрам: 1) ξ=2z/b; 2) η=a/b.
Метод угловых точек.
В результате сравнения численных решений оказалось, что напряжение под центром и под углом площади связанны следующим образом: σzугл/Z=0.25 σzцентр/(0,5z) Для определения вертикального напряжения σz в любой точке полупространства можно воспользоваться выражением σz=0.25αP, где α- коэфф., принимаемый в зависимости от отношения сторон площадей загружения a,b и глубины z.
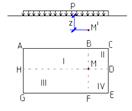
Если проекция рассматриваемой точки M’ на горизонтальную поверхность полупространства (точка М) располагается в пределах площади загружения, то эту площадь можно разбить на 4 прямоугольника (ABMH, BCDM, DEFM, FGHM) так, что бы точка M была угловой точкой каждого из них. Тогда напряжение σz найдем суммированием напряжений под угловыми точками четырех площадей загружения: σz= σz1+ σz2 + σz3 + σz4=0,25(α1+α2 +α3 +α4)P Так, пользуясь методом угловых точек, можно найти напряжение в любой точке полупространства, к поверхности которого приложена равномерно распределенная нагрузка в пределах прямоугольной площади.
11.Деформации основания Прогноз величины деформаций оснований на стадии проектирования сооружения позволяет выбрать наиболее правильные конструктивные решения фундаментов и надземных частей зданий и сооружений. Осадки оснований оказывают решающее влияние на прочность и устойчивость подземных конструкций. Осадкой называется медленная и сравнительно небольшая деформация, происходящая в результате уплотнения грунта под действием нагрузок и сопротивляющаяся коренным изменениям его структуры. При равномерных осадках основания подошва фундамента в любой моент времени опускается на одинаковую величину. Такие осадки не вызывают перераспределения усилий в конструкциях, но затрудняют нормальную эксплуатацию. При неравномерных осадках основания подошва фундамента опускается на разную величину, вызывая перераспределение усилий и деформаций в надземных частях зданий и сооружений. Такие осадки ухудшают эксплуатацию оборудования, изменяют условия устойчивости сооружений, вызывают перенапряжения в отдельных конструкциях и элементах. В зависимости от характера развития неравномерных осадок и от жесткости здания или сооружения возникают следующие виды деформаций. Прогиб и выгиб возникают в протяженных зданиях и сооружениях, не обладающих большей жесткостью. В случае развития прогиба (рис. 7.1,а) наиболее опасная зона растяжения находится в нижней части здания или сооружения, выгибе (см. рис. 7.1,6), — наоборот, в верхней части сооружения.
Рис. 7.1. Схема прогиба (а) и выгиба (б) сооружения Относительный прогиб или выгиб (ƒ/L) здания или сооружения оценивается отношением стрелы прогиба или выгиба к длине прогнувшейся части здания и кривизной изгибаемого участка (рис. 7.2) и определяется по формуле (по пособию к СНиП, 1986; СНиП 2.02.01—83):
где S1 и S3 — осадки в краях фундамента; S2 — наибольшая или наименьшая осадка фундамента; L — длина фундамента.
Рис. 7.2. Относительный прогиб или выгиб сооружения Крен (наклон) — поворот фундамента относительно горизонтальной оси, проявляющийся при несимметричной загрузке основания. Наибольшую опасность данный вид деформации представляет для высоких сооружений — дымовых труб, узких зданий повышенной этажности и др., т.е. характерен для жестких сооружений. Крен рассматривается как разность абсолютных осадок двух точек фундаментов, отнесенных к расстоянию между ними (рис. 7.3), и определяется по формуле
где S1 и S2 — осадки крайних точек сплошного фундамента или двух фундаментов.
Рис. 7.3. Крен сооружения Перекос зданий и сооружений характерен при резком проявлении неравномерности осадок на участке небольшой протяженности при сохранении относительной вертикальности несущих конструкций (рис. 7.4). Кручение возникает при неодинаковом крене здания или сооружения по длине, при этом происходит развитие крена в двух сечениях сооружения в разные стороны (рис. 7.5).
Рис. 7.4. Перекос сооружения
Рис. 7.5. Кручение сооружения
Рис. 7.6. Схема горизонтального перемещения устоя моста (а) и гидротехнического сооружения (б)
|



 7.1.
7.1.
 (7.2)
(7.2)