ЛАБОРАТОРНАЯ РАБОТА №3
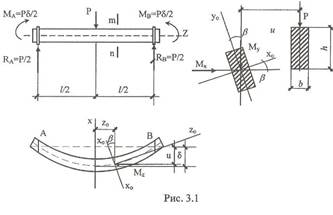
ИСПЫТАНИЕ ДЕРЕВЯННОЙ БАЛКИ НА УСТОЙЧИВОСТЬ ПЛОСКОЙ ФОРМЫ ИЗГИБА Целью работы является определение фактической величины критической нагрузки, при которой образец теряет устойчивость (плоскую форму изгиба), и сравнение ее с теоретически вычисленной. 3.1. Основные расчетные положения Теоретически величину критической нагрузки можно найти, рассмотрев деформированное состояние образца (рис. 3.1). Будем считать, что при деформации концы балки могут свободно вращаться относительно главных осей инерции X и Y; вращению их относительно оси Z препятствуют специальные устройства. При таких исходных положениях боковое выпучивание будет сопровождаться кручением. Положим, что произошло небольшое боковое выпучивание балки (рис. 3.1). Рассмотрим в таком состоянии часть балки вправо от сечения m - n. Внешними силами, действующими на эту часть, являются опорная реакция RB=P/2 и реактивный момент
Моменты относительно осей, имеющих начало в точке Д (в центре поперечного сечения) и параллельных осям X, Y и Z, будут равными:
Проекции этих моментов на оси Х0, Y0, Z0 имеют вид: (3.1) Дифференциальные уравнения равновесия: (3.2) Где
Е и G - модуль упругости и модуль сдвига древесины соответственно. Решение системы дифференциальных уравнений (3.2) дает следующее выражение для критической силы
где При закреплении балки от поворота только на опорах
|

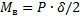 .
.




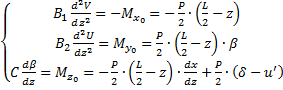
 – главные жесткости балки при изгибе,
– главные жесткости балки при изгибе,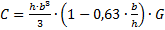 – жесткость балки при кручении,
– жесткость балки при кручении,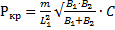 (3.3)
(3.3)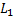 - длина полуволны; m - коэффициент, зависящий от расчетной схемы.
- длина полуволны; m - коэффициент, зависящий от расчетной схемы.


