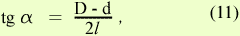Понятие о конусе и его элементах

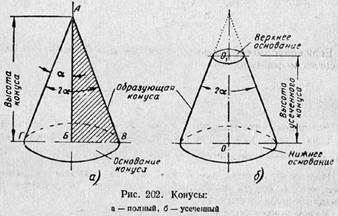
Элементы конуса. Если вращать прямоугольный треугольник АБВ вокруг катета АБ (рис. 202, а), то образуется тело АВГ, называемое полным конусом. Линия АБ называется осью или высотой конуса, линия АВ — образующей конуса. Точка А является вершиной конуса.

При вращении катета БВ вокруг оси АБ образуется поверхность круга, называемая основанием конуса.

Угол ВАГ между боковыми сторонами АВ и АГ называется углом конуса и обозначается 2α. Половина этого угла, образуемая боковой стороной АГ и осью АБ, называется углом уклона конуса и обозначается α. Углы выражаются в градусах, минутах и секундах.

Если от полного конуса отрезать его верхнюю часть плоскостью, параллельной егооснованию (рис. 202, б), то получим тело, называемое усеченным конусом. Оно имеет два основания верхнее и нижнее. Расстояние OO₁ по оси между основаниями называется высотой усеченного конуса. Так как в машиностроении большей частью приходится иметь дело с частями конусов, т. е. усеченными конусами, то обычно их просто называют конусами; дальше будем называть все конические поверхности конусами.

Связь между элементами конуса. На чертеже указывают обычно три основных размера конуса: больший диаметр D, меньший — d и высоту конуса l (рис. 203).

Иногда на чертеже указывается только один из диаметров конуса, например, больший D, высота конуса l и так называемая конусность. Конусностью называется отношение разности диаметров конуса к его длине. Обозначим конусность буквой K, тогда

Если конус имеет размеры: D =80 мм, d = 70 мм и l = 100 мм, то согласно формуле (10):

Это значит, что на длине 10 мм диаметр конуса уменьшается на 1 мм или на каждый миллиметр длины конуса разница между его диаметрами изменяется на

Иногда на чертеже вместо угла конуса указывается уклон конуса. Уклон конуса показывает, в какой мере отклоняется образующая конуса от его оси.
Уклон конуса определяется по формуле

где tg α — уклон конуса;
D — диаметр большого основания конуса в мм;
d — диаметр малого основания конуса в мм;
l — высота конуса в мм.

Пользуясь формулой (11), можно при помощи тригонометрических таблиц определить угол а уклона конуса.

Пример 6. Дано D = 80 мм; d=70мм; l= 100 мм. По формуле (11) имеем

По таблице тангенсов находим величину, наиболее близкую к tg α = 0,05, т. е. tg α = 0,049, которому соответствует угол уклона конуса α = 2°50'. Следовательно, угол конуса

2α = 2·2°50' = 5°40'.

Уклон конуса и конусность обычно выражают простой дробью, например: 1: 10; 1: 50, или десятичной дробью, например, 0,1; 0,05; 0,02 и т. д.