Переріз поверхні площиною окремого положення

Переріз поверхні площиною

 

При перерізах поверхонь площиною утворюється плоска крива лінія, кожна точка якої є точкою перетину лінії каркаса поверхні з січною площиною. Для побудови точок лінії перерізу можуть бути застосовані метод допоміжних січних площин та методи перетворення площин проекцій. Звичайно обирають допоміжні січні площини рівня або проекціювальні площини, що дає можливість визначити множину точок перетину ліній каркаса поверхні з допоміжною площиною. Способи перетворення площин проекцій дозволяють перевести площину загального положення в проекціювальне положення і цим спростити розв’язування задачі.

 

Переріз поверхні площиною окремого положення

 

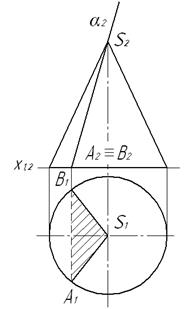
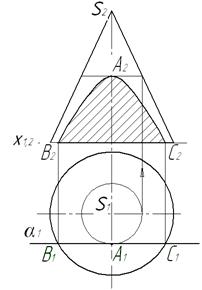
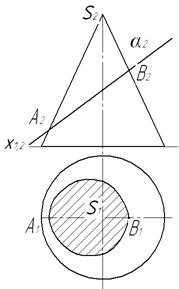
При перетині поверхні площиною окремого положення отримаємо плоску фігуру, що називається перерізом. Ця фігура належить січній площині.

Визначення проекцій лінії перерізу звичайно починають з побудови опорних точок – точок, розміщених на крайніх контурних твірних поверхні, найвищих і найнижчих точок фігури, точок, які визначають границю видимості. Після цього визначають довільні точки фігури перерізу.

Конічні перерізи. На поверхні прямого кругового конуса від перетину площиною можна отримати такі лінії:

1) дві твірні, якщо січна площина α проходить через вершину конуса (рис. 7.1, а);

2) коло, якщо січна площина α перпендикулярна до осі конуса (рис. 7.1, б);

а)	б)
Рисунок 7.1

 

3) гіперболу, якщо січна площина α; паралельна до двох довільних твірних конуса або якщо ця площина паралельна до осі конуса (7.2, а);

4) параболу, якщо січна площина α; паралельна до однієї з твірних конуса (рис. 7.2, б);

5) еліпс, якщо площина α; перетинає всі твірні конуса і вона не перпендикулярна до осі конуса (рис. 7.2, в).

 

а)	б)	в)
Рисунок 7.2