При отсутствии амплитудного ограничения входного колебания u c(t)выходное напряжение частотного детектора с расстроенными избирательными цепями или на основе аналогового перемножителя оказывается зависимым не только от значения φ(t), но и от величины U c. Этого недостатка лишен дробный частотный детектор, или детектор отношений (рис. 4.9).
Рис. 4.9. Схема дробного детектора
Дробный частотный детектор содержит два связанных контура – LC и LgCg, настроенных на среднюю частоту входного сигнала ωс, причем выходной контур LgCg включен по схеме со средней точкой и в обмотках его формируются противофазные напряжения – Ug /2. На резонансной частоте ω0 = ωс контуров LC и LgCg напряжение на втором контуре оказывается сдвинутым по фазе относительно напряжения на первом контуре на угол p/2. Напряжения на диодах VD 1 и VD 2, подключенных к контуру, определяются суммой напряжения с катушки Lg и напряжения U 0 с катушки связи L св и резистора R н. Эти напряжения можно представить в векторной форме (рис. 4.10) как
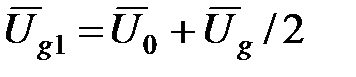 ,
,  . (4.13)
. (4.13)
При значении ω0 = ωс фазовый сдвиг между векторами 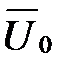 и
и 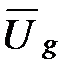 равняется величине p/2, и в этом случае
равняется величине p/2, и в этом случае 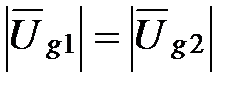 . При значениях ω0 < ωс имеем
. При значениях ω0 < ωс имеем 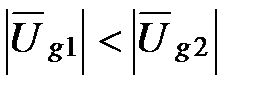 . При значениях ω0 > ωс получим следующее неравенство:
. При значениях ω0 > ωс получим следующее неравенство: 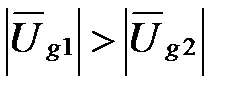 . Через диоды, работающие как амплитудные детекторы в режиме «сильных» сигналов, будет проходить ток, имеющий форму синусоидальных импульсов, в котором присутствуют переменная и постоянная составляющие. Пути прохождения этих составляющих различны.
. Через диоды, работающие как амплитудные детекторы в режиме «сильных» сигналов, будет проходить ток, имеющий форму синусоидальных импульсов, в котором присутствуют переменная и постоянная составляющие. Пути прохождения этих составляющих различны.
Переменная составляющая тока через диод VD 1 проходит по цепи C н(1), R н, L св, L g, а через диод VD 2 – по цепи C н(2), R н, L св, L g. Постоянная составляющая токов диодов VD 1 и VD 2 протекает по одной и той же цепи: VD 1, R 1, R 2, VD 2, Lg, поэтому величина постоянного тока через диоды оказывается одинаковой. Как следует из выражения (4.13) и рис. 4.10, при значении f c = f 0 имеем  . учитывая, что постоянный ток через диоды по величине одинаков, углы отсечки тока в обоих диодах также одинаковы (θ1 = θ2).
. учитывая, что постоянный ток через диоды по величине одинаков, углы отсечки тока в обоих диодах также одинаковы (θ1 = θ2).
Рис. 4.10. Векторные диаграммы напряжений на диодах дробного детектора
При | Ug 1| ¹ | Ug 2| равенство этих токов может быть обеспечено при соответствующем изменении угла отсечки токов через диоды, а именно при | Ug 2| > | Ug 1| имеем θ1 > θ2. Если | Ug 2| < | Ug 1|, то θ1 < θ2. Следовательно, в дробном детекторе при изменении частоты сигнала изменяются углы отсечки токов диодов.
Выходное напряжение дробного детектора может быть записано в виде
U вых = U =(2) – (U =(1) + U =(2))/2 = (U =(2) – U =(1))/2. (4.14)
Выражение (4.14) можно переписать в форме
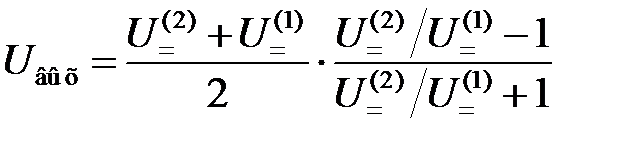 . (4.15)
. (4.15)
Выбирая постоянную времени исходя из следующего неравенства: C 0(R 1 + R 2) >> 1/Wmin, где Wmin – минимально возможная частота паразитной амплитудной модуляции, можно обеспечить практически постоянное значение суммы U =(1) + U =(2) в формуле (3.15). В отношении U =(2)/ U =(1) этой же формулы числитель и знаменатель изменяются одинаково при колебаниях амплитуды входного сигнала. Указанные обстоятельства обеспечивают малую чувствительность дробного детектора к изменению величины входного сигнала вследствие паразитной амплитудной модуляции.

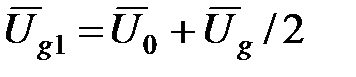 ,
,  . (4.13)
. (4.13)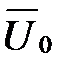 и
и 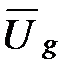 равняется величине p/2, и в этом случае
равняется величине p/2, и в этом случае 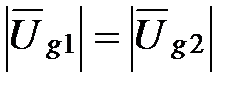 . При значениях ω0 < ωс имеем
. При значениях ω0 < ωс имеем 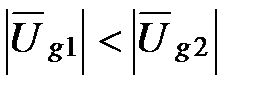 . При значениях ω0 > ωс получим следующее неравенство:
. При значениях ω0 > ωс получим следующее неравенство: 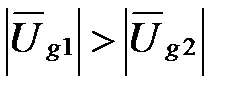 . Через диоды, работающие как амплитудные детекторы в режиме «сильных» сигналов, будет проходить ток, имеющий форму синусоидальных импульсов, в котором присутствуют переменная и постоянная составляющие. Пути прохождения этих составляющих различны.
. Через диоды, работающие как амплитудные детекторы в режиме «сильных» сигналов, будет проходить ток, имеющий форму синусоидальных импульсов, в котором присутствуют переменная и постоянная составляющие. Пути прохождения этих составляющих различны. . учитывая, что постоянный ток через диоды по величине одинаков, углы отсечки тока в обоих диодах также одинаковы (θ1 = θ2).
. учитывая, что постоянный ток через диоды по величине одинаков, углы отсечки тока в обоих диодах также одинаковы (θ1 = θ2).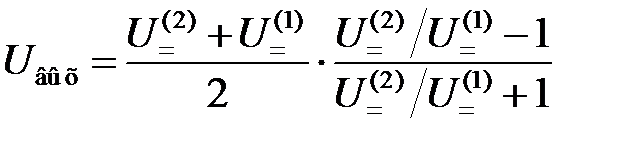 . (4.15)
. (4.15)


