Напряжение на конденсаторе С равно выходному напряжению источника
Так как
где Величина
называется емкостным сопротивлением цепи. (Индекс С при обозначении тока указывает лишь на то, что он протекает в цепи с чисто емкостной нагрузкой). Для постоянного тока w=0, поэтому конденсатор представляет бесконечно большое сопротивление. С ростом частоты переменного тока емкостное сопротивление уменьшается. Из сравнения формул (9) и (1) видно, протекающий через конденсатор ток опережает по фазе напряжение на емкости на p/2. (рис. 4, б). На векторной диаграмме (рис. 4, в) вектор тока ICm повернут на угол p/2 от UCm в сторону положительного направлению вращения. Сопротивления XC и XL называют реактивными. На них не происходит превращения энергии электрического тока во внутреннюю энергию нагрузки несмотря на наличие сопротивления (в этом смысл их названия). 4.Рассмотрим электрическую цепь с сосредоточенными параметрами R,L,C (рис. 5, а). Под действием переменного напряжения UВХ в цепи установится переменный ток I, величина которого одинакова во всех элементах – резисторе, катушке и конденсаторе, так как они соединены последовательно (ток через каждый из вольтметров считаем пренебрежимо малым по сравнению с I). Протекающий ток вызывает на них падение напряжения: Для расчета цепей переменного тока применяются два метода: 1)так называемый символический – это аналитический метод с использованием комплексных переменных [1,3,4] и 2) графический – метод векторных диаграмм. Воспользуемся вторым [3]. Построение векторной диаграммы для последовательного контура производится в следующем порядке. 1.В произвольном направлении, например горизонтально, прочерчивают ось токов и на ней в определенном масштабе откладывают вектор тока Im. Вместо амплитудного значения можно откладывать эффективное, 2.В том же направлении откладывают вектор UR, – падение напряжения на активном сопротивлении, которое синфазно току. Масштаб для напряжения должен быть выбран, разумеется, свой. 3.Под углом -p/2 к вектору тока строят вектор UC, так как напряжение на конденсаторе отстает от тока по фазе на эту величину. 4.Под углом +p/2 к оси токов проводят вектор UL, так как напряжение на индуктивности опережает ток по фазе.
Рис.5
5.Находят векторную сумму всех напряжений, получается вектор UВХ. Видно, что ток в цепи I не совпадает по фазе с приложенным к ней напряжением UВХ (рис. 5, б). j – разность фаз тока и напряжения (по-другому, сдвиг фаз между током и напряжением). 6.Измерение длины суммарного вектора с учетом масштаба напряжения дает входное напряжение в вольтах, а угол сдвига фаз измеряется на диаграмме транспортиром или вычисляется тригонометрически. В этом состоит графический способ расчета цепи. Итак, если напряжение на входе цепи изменяется по закону Аналитически величины Im и j определяются следующим образом.
|

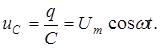 (8)
(8)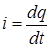 и
и  , то
, то 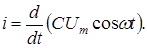
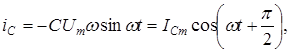 (9)
(9)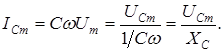 (10)
(10) (11)
(11) – на активном сопротивлении,
– на активном сопротивлении,  – на индуктивности и
– на индуктивности и  – на емкости. Величинами UR, UL, UC, UВХ обозначены напряжения, которые показывают соответствующие вольтметры. Сумма напряжений должна быть равна приложенному к данной цепи напряжению UВХ. Но эта сумма не может быть ни арифметической, ни алгебраической, а только векторной, так как между напряжениями существует фазовые сдвиги.
– на емкости. Величинами UR, UL, UC, UВХ обозначены напряжения, которые показывают соответствующие вольтметры. Сумма напряжений должна быть равна приложенному к данной цепи напряжению UВХ. Но эта сумма не может быть ни арифметической, ни алгебраической, а только векторной, так как между напряжениями существует фазовые сдвиги.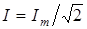 , т.е. показание прибора. Это эквивалентно уменьшению масштаба диаграммы в
, т.е. показание прибора. Это эквивалентно уменьшению масштаба диаграммы в  раз.
раз.
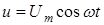 , то в цепи течет ток
, то в цепи течет ток  , причем разность фаз j может быть как положительной, так и отрицательной.
, причем разность фаз j может быть как положительной, так и отрицательной.


